mat cau

TRƯỜNG THPT BA BỂ - BẮC BẠN
TRƯỜNG THPT BA BỂ - BẮC BẠN
TỔ: TOÁN - TIN
TỔ: TOÁN - TIN
O
Mọi điểm M nằm trên C(O;R)
thì OM =
A
B
M
O
C(O;R) = {M | OM = R} (R>0)
R
OM = R (bán kính)
AB = 2R (đường kính)
C
Tam giác ABC là tam giác vuông tại C
O
OA
3
>R
A
3
A
2
OA
2
=R
A
1
OA

1
<R
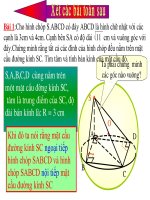
Xác định vị trí của điểm A trong
các trường hợp sau với đường tròn
C(O;R)
+ OA
2
= R
+ OA
3
> R
+ OA
1
< R
Cho đường tròn C(O;R).
R
C¸c m« h×nh thùc tÕ
1. Mặt cầu.
Định nghĩa: Cho một điểm O cố định và một số thực dương R. Tập hợp
tất cả những điểm M trong không gian cách điểm O một khoảng bằng
R được gọi là mặt cầu tâm O bán kính R.
A
3
O
A
5
A
2
A
1

A
4
R
R
R
R
R
Vy mt mt cu xỏc nh khi bit
tõm v bỏn kớnh ca nú.
Kí hiệu: Mặt cầu tâm O bán kính R là S(O;R) hay (S):
V y: S(O;R) S(O;R) = {M|OM=R}
Nếu OA = R thì v trí điểm A so với mặt cầu S(O;R) như
thế nào ?
Nếu OA = R thì điểm A nằm trên mặt cầu
Nếu OA < R thì điểm A nằm
trong mặt cầu
Hình biểu diễn vị trí tương
đối của điểm A với mặt cầu
Nếu OA > R thì điểm A nằm
ngoài mặt cầu
OA
2
<R
OA
1
=R
OA
3
>R
Nếu OA < R thì v trí điểm A so với mặt cầu S(O;R) như

thế nào ?
Nếu OA > R thì v trí điểm A so
với mặt cầu S(O;R) như thế nào ?