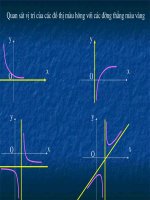
sự đồng biến và nghịch biến của hàm số ( T12 cua Vân - THĐ - HP)

Bài I;Khẳng định:
.Các

hàm số sau đây luôn đồng biến trên từng khoảng xác định
của nó.Đúng hay sai?
1) y = tgx

2) y = cotgx

§

S

3) y = 1 – 3x S

π x
6)y = (
)
2
7) y =(

e )

§

x

3

S

8) y = ex

§

4) y = lgx

§

9) y = log0,5(1- x)

§

5)y = lnx

§

10) y = 3

S

2 -5x


Chương II:ứng dụng của đạo hàm

Tiết 1: sự Đồng biến, nghịch biến
của hàm số


I .Nhắc lại định nghĩa Hàm Số đồng biến, nghịch biến

Cho hàm số f(x) xác định trên (a;b)
1. f(x) đồng biến trên ( a ;b ) x1,,x2 (a;b) và x1< x2 => f(x1) < f(x2)
A

2. f(x) nghịch biến trên ( a ;b ) x1,,x2 ∈ (a;b) vµ x1< x2 => f(x1) > f(x2)
y y = f(x)
y = f(x)
y
A

O

a

b

x

x

O
b

a


Nhận xét
ã f(x) đồng biến trên (a;b) => f (x) = lim y 0 trên (a;b)
0 x

ã f(x) ngh biÕn trªn (a;b) => f ’(x) = lim ∆y ≤ 0 trên (a;b)
0 x

Giới hạn này
Chiều ngược
có là điều kiện
lại có đúng
đủ của tính đơn
không?
điệu?


2.Điều kiện đủ của tính đơn điệu
Định lý Lagrăng:
Nếu hàm số f(x) liên tục trên đoạn [a;b]
có đạo hàm trên khoảng (a;b)
Thì tồn tại c (a;b) sao cho f(b) f(a) = f’( c )(b – a)
Hay

f(b) – f(a)
f (c)=
b-a
y
’

f(b) – f(a)
f (c)=
b-a

d

∆

’

C

f(c)

B

kd = f ‘ (c)
kAB =

f(b) – f(a)
b-a

f(a)
O

A
a

c

b

x


ý nghĩa hình học của định lý Lagrăng (sgk)

Cho hàm số y = f(x) thoả mÃn định lý Lagrăng đồ thÞ ( C )
A ; B ∈ ( C ) = > ∃ C (c; f (c) )∈ cung AB sao cho tiÕp tuyÕn t¹i C // AB
d
y
∆
C

f(c)
f(a)
O

B

A
a

c

b

x


Định lý 1Cho hàm số y = f (x) có đạo hàm trên khoảng (a;b).
a)Nếu f (x) > 0 với mọi x (a;b) thì hàm số f(x) đồng biến trên
khoảng đó.
b)Nếu f (x) < 0 với mọi x (a;b) thì hàm số f(x) nghịch biến trên
khoảng đó.
Chứng minh a áp dụng định lý Lagrăng

thoả mÃn trên tập [x1;x2]

y
f(b)
f(x2)
f(x1)
f(a)
O

a

x1

x2

b

> ∃ c ∈ (x1;x2) sao cho
f(x2) – f(x1) = f ’( c) (x2 – x1)
Do f ’ (x) > 0 /(a;b) =>
f ’ (x) > 0 / (x2 –x1) =>
x f ’ (c ) > 0 l¹i do x2 – x1> 0
=> f (x2) > f (x1) …


Định lý 1 Cho hàm số y = f (x) có đạo hàm trên khoảng (a;b).
a)Nếu f (x) > 0 với mọi x (a;b) thì hàm số f(x) đồng biến trên
khoảng đó.
b)Nếu f (x) < 0 với mọi x (a;b) thì hàm số f(x) nghịch biến trên
khoảng đó.

Mở rộng
Định lý 2 Cho hàm số y = f (x) có đạo hàm trên khoảng (a;b).
Lợi ích của định
a)Nếu f ’ (x) ≥ 0 víi mäilý ®iỊu kiƯn ®đ sè f(x) đồng biến trên
x (a;b) thì hàm
mở rộng?
khoảng đó.(Đẳng thức chỉ xảy ra tại hữu hạn điểm)
b)Nếu f (x) 0 với mọi x (a;b) thì hàm số f(x) nghịch biến trên
khoảng đó.( Đẳng thức chỉ xảy ra tại hữu hạn điểm)
Định lý 2 định lý 1 n t n?


Ví dụ 1: Tìm khoảng đồng biến hay nghịch biến của hàm số sau
y = x2 4x +6
Bài giải

Tập xác định: D = R
Chiều biến thiên:
y = 2x 4 ,
Giải phương trình y = 0 2x 4 = 0 x = 2
Dấu y

X



2

+

y

-

0

+

Hàm số luôn luôn đồng biến trên khoảng ( 2 ;+)
Và nghịch biến trên kho¶ng (-∞ ; 2)


Ví dụ 2: Tìm khoảng đồng biến hay nghịch biến của hàm số sau
y = x3 3x2 +6
Bài giải

Tập xác định: D = R
Chiều biến thiên:
y = 3x2 6x ,
Giải phương trình y = 0 3x3 6x = 0 x = 0 v x = 2
DÊu y

X



0

y

+

0

2
-

+

0

+

Hàm số luôn luôn đồng biến trên các khoảng ( - ; 0) ;(2;+)
Và nghịch biến trên khoảng (0; 2)


Ví dụ 3: Tìm khoảng đồng biến hay nghịch biến cđa hµm sè sau
y = - x4 + 2x2 +6
Bµi giải

Tập xác định: D = R
Chiều biến thiên:

y = - 4x3 +4x ,
Giải phương trình y = 0 -4x3 + 4x = 0 x = 0 v x = 1
Dấu y

X

-

-1

y

-

0

0
+

0

1
-

0

+
+

Hàm số luôn luôn đồng biến trên các khoảng ( - ; 0) ;(2;+)
Và nghịch biến trên khoảng (0; 2)


Ví dụ 4: Xác định chiều biến thiên của hàm số:

3

y = 3x + = 5
x

Nêu Quy
tắc xác
định chiều
biến thiên
của hàm
số

Bài giải:

*Tập xác định: D = (-;0)(0;+)
3( x 2 )
1
* Đạo hàm y =
x2

y = 0 x = 1

X



y

+

-1 0
0

1

-|| - 0

Hàm số đồng biến trên các khoảng (-;-1) ;(1;+)
Hàm số nghịch biến trên các khoảng (-1;0) ;(0;1)

+
+


3.Điểm tới hạn.
Định nghĩa: Cho hàm số y = f(x) xác định trên khoảng (a;b) và
x0 (a;b).Điểm x0 được gọi là một điểm tới hạn của hàm số f(x)
Nếu tại đó f (x) không xác định hoặc x0 là nghiệm của phương trình
f (x) = 0.
Qui tắc: ãTìm tập xác định của hàm số
ãTìm điểm tới hạn của hàm số
ãxét dấu f (x)
ãKết luận về khoảng đồng biến , nghịch biến theo định lý


Bài tập về nhà.
Từ bài 1 đến hết bài 4 sgk / Tr52 ,53