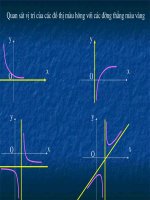
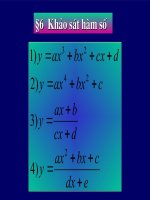Khảo sát hàm bậc ba ( t12- của Vân -THĐ HP)

2
•
1)Tập xác định.
•
2)Chiều biến thiên của hàm số.
•
*)Sự đồng biến và nghịch biến và cực trị
của hàm số.
•
*)Tính lồi lõm và điểm uốn của đồ thị.
•
*)Giới hạn của hàm số.Tiệm cận của đồ thị.
•
*)Bảng biến thiên của hàm số.
•
3) Đồ thị của các hàm số.
3
1)Tập xác định.
2)Chiều biến thiên của hàm số.
*)Sự đ.biến và ng biến và cực trị (nếu có) của hàm số.
+) Tìm y’ => Xét dấu y’ =>Kết luận về khoảng đồng biến,
nghịch biến và cực trị (nếu có ) của hàm số.
*)Tính lồi lõm và điểm uốn của đồ thị.
+)Tìm y” => xét dấu y” => kết luận về khoảng lồi, lõm và
điểm uốn (nếu có) của đồ thị hàm số .
*)Tìm giới hạn của hàm số khi x dần tới vô cực hoặc khi
dần tới các giá trị hàm số không xác định.Tiệm cận (nếu
có) của đồ thị.
*)Bảng biến thiên của hàm số.
+)Tổng hợp tất cả các vấn đề trên vào một bảng.
3) Đồ thị của các hàm số.

Lấy điểm cực trị, điểm uốn(nếu có) và giao của đồ thị với
ox,oy, một số điểm khác nữa của đồ thị =>tổng hợp vào
một bảng để dễ kiểm soát khi vẽ.
SƠ ĐỒ KHẢO SÁT HÀM SỐ:
4
Khảo sát hàm số
Đa thức
Phân thức
hữu tỷ
edx
cbxax
y
+
++
=
2
edx
bax
y
+
+
=
y= ax
3
+bx
2
+cx+d
y = a x
4
+bx

2
+c
CÁC HÀM SỐ ĐƯỢC NGHIÊN CỨU TRONG LỚP 12
5
1)Tập xác định.
2)Chiều biến thiên của hàm số.
*)Sự đ.biến và ng biến và cực trị (nếu có) của hàm số.
+) Tìm y’ => Xét dấu y’ =>Kết luận về khoảng đồng biến,
nghịch biến và cực trị (nếu có ) của hàm số.
*)Tính lồi lõm và điểm uốn của đồ thị.
+)Tìm y” => xét dấu y” => kết luận về khoảng lồi, lõm và
điểm uốn (nếu có) của đồ thị hàm số .
*)Tìm giới hạn của hàm số khi x dần tới vô cực hoặc khi
dần tới các giá trị hàm số không xác định.Tiệm cận (nếu
có) của đồ thị.
*)Bảng biến thiên của hàm số.
+)Tổng hợp tất cả các vấn đề trên vào một bảng.
3) Đồ thị của các hàm số.
Lấy điểm cực trị, điểm uốn(nếu có) và giao của đồ thị với
ox,oy, một số điểm khác nữa của đồ thị =>tổng hợp vào
một bảng để dễ kiểm soát khi vẽ.
S KH O S T H M SƠ ĐỒ Ả Á À Ố ®a thøc
6
a < 0
∆
> 0
{
a < 0
∆
< 0

{
a < 0
∆
=0
{
y’ = 3ax +2bx +c,
2
Có bao nhiêu khả năng
khi xét dấu đạo hàm?
3 khả năng
4 khả năng
6 khả năng
a > 0
∆
> 0
{
a > 0
∆
< 0
{
a > 0
∆
= 0
{
y = ax
3
+ bx
2
+ cx + d
,

= b
2
– 3ac
CÁC DẠNG BÀI KHẢO SÁT HÀM SỐ:
7
8
1)Tập xác định : D = ?
2)Sự biến thiên :
a)Khoảng đb, ngb và cực trị.
-
∞

y’
x
+
-
0
0
- 2 0
+
∞
+
Hàm số đb trên
∞∞
;- 2)
và
-
(0;+
(
)

Và nb trên (- 2;0)
y
CĐ
= 0x
CĐ
= - 2
Tại Hàm số đạt
y
CT
= - 4
x
CT
= 0
Tại Hàm số đạt
b)Khoảng lồi lõm và điểm uốn.
Đồ thị hàm số :
∞
Lồi trên khoảng (-
- 1)
;
∞
Lõm trên khoảng (- 1;+
)
Tại x = - 1 đồ thị có
điểm uốn I(- 1;- 2)
c)Giới hạn
d) Bảng biến thiên
∞
+
∞

∞
x
y’
-
∞

- 2 0
0
0
++
-
y
-
+
y
CĐ
= 0
y
CT
= - 4
3) Đồ thị
;
=
−∞→
y
x
lim
=
+∞→
x

lim
-∞
+∞
1)Tập xác định : D = R
y = x
3
+ 3x
2
- 4
KHẢO SÁT HÀM SỐ:
.y’ = 3x
2
+6x,y’ = 0  x = - 2,x = 0
y” = 6x + 6 , y” = 0  x = -1
∞
- 1x
+
-
0
+
∞
y”
43
444546
9

A
- 3
B
1

- 4
0

I
T
- 2
- 1
0
0
- 2
- 4
im
x
y
Bng ta mt s im c bit ca th.
y = x
3
+ 3x
2
- 4
TH HM S:
Vẽ hệ trục tọa độ





X
Y
-3

-2 -1 0 1
-2
-4
A
đ
I
t
b
Vẽ đồ thị
đồ thị nhân điểm uốn làm tâm đối xứng




10
10
11
y’ = 3x
2
- 6x + 4
ta có a = 3 > 0,
=> y’ > 0,
0
'
<∆
Rx
∈∀
1)Tập xác định : D = R
2)Sự biến thiên :
3) Đồ thị

a)Khoảng đb, ngb và cực trị.
b)Khoảng lồi lõm và điểm uốn
d) Bảng biến thiên
c)Giới hạn
x
y”
-
∞
+
∞
1
0
- +
Đồ thị hàm số :
Tại x = 1
Đồ thị có điểm uốn I(1;1)
−∞=
−∞→
y
x
lim
+∞=
+∞→
y
x
lim
;
∞
x
y’

+
y
-
+
∞
∞
-
∞
∞
Lồi trên khoảng (- ; 1)
∞
y = x
3
- 3x
2
+4x - 1
KHẢO SÁT HÀM SỐ:
Lõm trên khoảng ( 1; + )
∞
=> Hàm số luôn đồng biến.
không có cực trị
y’’= 6x- 6, y” = 0  x = 1
43
444548
12
y = x
3
- 3x
2
+ 4x - 1

TH HM S:
Vẽ hệ trục tọa độ
.
.
1 2
0
-1
.
.
1
2
.
.
3
.
1/2
.
3/2
.
3/8
.
13/8
y
x
.
.
Các điểm đặc biệt
điểm uốn I ( 1 ; 1)
.
I

điểm C( 1/2 ; 3/8 )
.
C
điểm A( 0 ; -1)
A
điểm D ( 3/2 ; 13/8 )
.
D
điểm B ( 2 ; 3)
.
B
Vẽ đồ thị
đồ thị nhân điểm uốn làm tâm đối xứng
13
Xin chµo
14
1)Tập xác định: D = R.
2)Sự biến thiên.
a)Khoảng đb , nb và cực trị.
y’ = - 3x
2
+ 6x - 3
y’ = 0 x= 1(nghiệm kép).
lại có a = - 3 < 0 =>
=>
H số nghịch biến trên R
=> không có cực trị
0=∆
Rxy
∈∀≤

,0'
b) Khoảng lồi lõm,điểm uốn.
y”=- 6x+6, y” = 0  x = 1.
Đồ thị hàm số :
Låi trên khoảng ( 1; + )
∞
Lâm trên khoảng (-
; 1)
∞
Tại x = 1
đồ thị có điểm uốn I(1;1)
x
y’
y
+
-∞
+∞
-
∞
∞
1
0
-
-
-
∞
∞
1
x
y”

+
0
-
+
c)Giới hạn.
;
?=
−∞→
y
x
lim
?=
+∞→
x
lim
3) Đồ thị.
d) Bảng biến thiên.
;
=
−∞→
y
x
lim
=
+∞→
x
lim
-∞
+∞
y = - x

3
+ 3x
2
– 3x + 2
KHẢO SÁT HÀM SỐ:
43
444549
15
y = - x
3
+3x
2
3x + 2
TH HM S:
Vẽ hệ trục tọa độ


x
-1
0
1 2
3

y
-7
1
2
9
Các điểm đặc biệt
điểm uốn I ( 1 ; 1)
I
.
điểm A( 0 ; 2)
A
điểm B ( - 1 ; 9)
.
B
.
điểm C( 2 ; 0)
C
điểm D ( 3 ; -7)
D
đồ thị nhân điểm uốn làm tâm đối xứng
Vẽ đồ thị

16
N
g
h
Ø

g
i
¶
i

l
a
o


t
r
o
n
g

Ý
t

p
h
ó
t
17

x
y’
∞
- +
∞
- 2
0
0
0
+
-
-
1)Tập xác định: D = R.
2)Sự biến thiên.
a)Khoảng đb , nb và cực trị.
y’ = - 3x
2
– 6x
y’ = 0 x=- 2,x = 0
H/số ng biến trên( -2;0)
Đg biến trên (- ;-2); (0; )
x = - 2 =>y
ct
= 2,x= 0 =>y
cd
= 6
b) Khoảng lồi lõm và điểm uốn.
y”=- 6x-6, y” = 0  x = -1.
∞
∞

Đồ thị lõm trên
(- ∞;-1)
Đồ thị lồi trên
(-1;+ ∞)
Điểm uốn I(-1;4)
c)Giới hạn.
−∞=+∞=
+∞→−∞→
yy
xx
lim;lim
d) Bảng biến thiên.
x
y’
∞
-
+
∞
- 2
0
0
0
+
-
-
y
y
ct
= 0
y

cd
= 4
+∞
-∞
3) Đồ thị.
-
∞
∞
-1x
y”
+
0
-
+
y =- x
3
-3x
2
+ 6
KHẢO SÁT HÀM SỐ:
43
444550
18
B
1
2
T
I
Đ
- 2

- 1
0
2
4
6
Điểm
x
y
A
-3
6
Bảng toạ độ một số điểm của đồ thị hàm số.
y =- x
3
-3x
2
+ 6
ĐỒ THỊ HÀM SỐ:
O
A
t
®
B
•
•••
x
-3
-1-2
1
y

4
2
6
•
•
•
•
I
®å thÞ nh©n ®iÓm uèn lµm t©m ®èi xøng
19
10
20
y = x
3
+ 1
1)Tập xác định:
2)Chiều biến thiên.
3) Đồ thị.
a) Tìm khoảng biến thiên và cực trị của hàm số.
b) Tìm khoảng lồi lõm và điểm uốn của đồ thị hàm số.
d) Lập bảng biến thiên.
D = R
Hàm số luôn luôn đồng biến => không có cực trị
y” = 6x, y” = 0 6x = 0  x =0
y” >0 x > 0 => đồ thị lõm trên (0;+ )
∞
∞
y” < 0 x < 0 => đồ thị lồi trên (- ;0 )
=>Điểm uốn I(0;1)
+

∞
∞
x
y’
-
∞

+
y
-
+
∞
0
0
+
c)Tìm giới hạn của hàm số.
KHẢO SÁT HÀM SỐ:
y’ = 3x
2
,y’ > 0,
A
x
R
∈
43
444551
=
−∞→
y
x

lim
=
+∞→
x
lim
-∞
+∞
;
21
y = x
3
+ 1
TH HM S:
Vẽ hệ trục tọa độ


x
-1
0
1 2

y
-7
1
2
9

-2
Các điểm đặc biệt
điểm uốn I ( 0 ; 1)
I
điểm C ( -1 ; 0)
C
điểm D ( -2 ; -7)
D
điểm B ( 1 ; 2)
B
.
điểm A( 2 ; 9)
.
A
Vẽ đồ thị
đồ thị nhân điểm uốn làm tâm đối xứng
22
23

1)Tập xác định : D = R
2)Sự biến thiên :
a)Khoảng đb, ngb và cực trị.
463
2
−+−
xx
y’ =
Ta có a = - 3,
∆
= -12 < 0
=>y’ < 0,
∀
x
∈
R
=>Hàm số luôn nb trên TXĐ
=> Không có cực trị
b)Khoảng lồi lõm và điểm uốn.
y’’=- 6x+6,
⇔
y’’= 0 x = 1
x
y”
-
∞
+
∞
1
0

+ -
Đồ thị hàm số :
Lõm trên khoảng (-
∞
; 1)
∞
Lồi trên khoảng (1; +
)
Tại x = 1 đồ thị có
điểm uốn I( 1;0)
c)Giới hạn
+∞=
−∞→
y
x
lim
−∞=
+∞→
x
lim
d) Bảng biến thiên
∞
+
∞
∞
x
y’
-
∞

-
y
-
+
y = - x
3
+ 3x
2
– 4x + 2
KHẢO SÁT HÀM SỐ:
43
444552
24
TH HM S:
.
.
1 2
0
-1
.
.
1
2
.
.
1/2
.
3/2
.
5/8

.
y
x
.
-5/8
-2
.
y = - x
3
+ 3x
2
4x + 2
Vẽ hệ trục tọa độ
Các điểm đặc biệt
điểm uốn I ( 0 ; 1)
I
điểm A( 1/2 ; 5/8 )
.
A
điểm B( 0 ; 2)
B
điểm C ( 3/2 ; -5/8 )
.
C
điểm D ( 2 ; -2)
Vẽ đồ thị
.
D
đồ thị nhân điểm uốn làm tâm đối xứng
25

10
26
Hình 1
Hình 2 Hình 3
Hình 4
Hình 5
Hình 6
y
y = ax
3
+bx
2
+cx +d có y’ = 3ax
2
+2bx +c,
= b
2
– 3ac
,
Điền dấu của a và vào mỗi hình vẽ cho đúng?
,