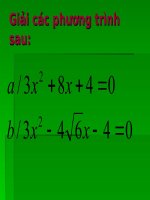bài 5: Công thức nghiệm thu gọn

KIỂM TRA BÀI CŨ
Bảng tóm tắt về công thức nghiệm thu gọn của phương trình bậc hai
Đối với phương trình ax
2
+ bx + c = 0 (a ≠ 0) và biệt thức = b
2
– 4ac :
Nếu > 0 thì phương trình có hai nghiệm phân biệt :
Nếu = 0 thì
Nếu < 0 thì
Giải phương trình
Với a = 7; b = -6 ; c = 2
Tính = b
2
– 4ac
= (-6 )2-4.7.2
=72 – 56 = 16 > 0
=> = 4
Vậy phương trình có 2 nghiệm phân biệt
∆
∆
∆
a
b
x
2
1
∆+−
=

a
b
x
2
2
∆−−
=
a
b
xx −==
21
02267
2
=+− xx
phương trình có nghiệm kép
∆
∆
∆
phương trình vô nghiệm.
2
7
223
7.2
426
2
;
7
223
7.2
426

2
21
−
=
−
=
∆−−
=
+
=
+
=
∆+−
=
a
b
x
a
b
x
2


BÀI : 5 . CÔNG THỨC NGHIỆM THU GỌN
?1/
48
Từ bảng kết luận của bài trước hãy dùng các đẳng thức
b=2b’ và để suy ra những kết quả sau :

Nếu >0 thì phương trình có hai nghiệm phân biệt


Nếu = 0 thì phương trình có nghiệm kép

Nếu < 0 thì phương trình vô nghiệm .
'4∆=∆
Đối với phương trình ax
2
+ bx + c = 0 (a≠0) và b =2b’,
:''
2
acb −=∆
'∆
a
b
x
a
b
x
''
;
''
21
∆−−
=
∆+−
=
'∆
a
b
xx

'
21
−==
'∆

II/ ÁP DỤNG
?2/ Giải phương trình 5x
2
+ 4x – 1 = 0 bằng cách điền vào
những chỗ trống :
GIẢI
a = ; b’ = ; c =

Nghiệm của phương trình :
'
''
2
∆
=−=∆ acb
1
5
32''
5
1
5
32''
2
1
−=
−−

=
∆−−
=
=
+−
=
∆+−
=
a
b
x
a
b
x
5 2 -1
39
09)1.(5)2(
2
==
>=−−

?3/49 Xác đònh a,b’,c rồi dùng công thức
nghiệm thu gọn giải phương trình :
02267);0483)
22
=+−=++ xxbxxa
'
''
2
∆⇒

−=∆ acb
2
3
24''
3
2
3
24''
2
1
−=
−−
=
∆−−
=
−
=
+−
=
∆+−
=
a
b
x
a
b
x
GIẢI
a)3x
2

+ 8x + 4 = 0
Với a= ; b = ; c =
Tính
Vậy : Nghiệm của phương trình :
3
4 4
24
044.3)4(
2
==
>=−=