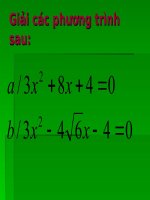Công thức nghiệm thu gọn

GIÁO ÁN ĐIỆN TỬ
MÔN : ĐẠI 9, TIẾT 55
GV . Thực hiện: Đỗ Thanh Bình
Tháng 11 năm 2008.

Áp dụng công thức nghiệm giải các phương trình sau :
Áp dụng công thức nghiệm giải các phương trình sau :
KiÓm tra bµi cò
KiÓm tra bµi cò
Gi¶i
a) Giải phương trình 5x
2
+ 4x – 1 = 0
(a = 5; b = 4 ; c = -1)
Ta có: Δ = 4
2
- 4.5.(-1)
= 16 + 20
= 36
Do Δ = 36 > 0 nên phương trình có hai nghiệm phân biệt:
1
4 36 4 6
2.5 1
x
50
1− + − +
= = =
2
4 36 4 6

2.5 0
x 1
1
− − − −
= = −=
a) 5x
a) 5x
2
2
+ 4x – 1 = 0
+ 4x – 1 = 0 ;
2
x 2 3x 3 0+ + =
b)
Do Δ = 0 nên phương trình có nghiệm kép :
b) Giải phương trình
2
x 2 3x 3 0+ + =
(a = 1; b = ; c = 3)
2 3
Ta có:
2
(2 3) 4.1.3∆ = −
= 12 - 12
= 0
1 2
2 3
2.1
x x 3
−

= == −

Qua phần kiểm tra bài cũ, ta đã giải hai phương trình :
Qua phần kiểm tra bài cũ, ta đã giải hai phương trình :
a) 5x
a) 5x
2
2
+
+
4
4
x – 1 = 0
x – 1 = 0 ;
2
x x2 3 3 0+ + =
b)
Hệ số b của hai
phương trình
trên có điều gì
đặc biệt ?
Còn cách giải nào
nhanh hơn không ?

Δ’ < 0
……………..
(7)
Phương trình ax
2
+ bx + c = 0 (a≠0) trong nhiều trường hợp ta đặt b = 2b’ (b’ =

b:2) thì
Δ = b
2
– 4ac =
Kí hiệu : Δ’ = b’
2
– ac
ta có : Δ = 4Δ’
§5. Công thức nghiệm thu gọn
1. Công thức nghiệm thu gọn.
b
2a
− − ∆
=
x
2
=

Nếu ∆ > 0 thì ∆’ > 0 , phương trình có hai nghiệm phân biệt :
x
1
= x
2
=
b
2a
− =
Dựa vào đẳng thức Δ = 4Δ’
Hãy nhận xét về dấu của Δ và ∆’ ?
?1 SGK.

=
b 2b' 4 ' 2b' 2 ' 2( b' ')
2a 2a 2a 2a
− + ∆ − + ∆ − + ∆ − + ∆
= = = =
x
1
=
=
=
=
Hãy điền vào chổ …… trong phiếu học tập theo mẫu sau :
2b' 4 '
2a
− − ∆
2b' 2 '
2a
− − ∆
2( b' ')
2a
− − ∆
b' '
a
− − ∆
2b'
2a
−
b'
a
−


Nếu ∆ = 0 thì , phương trình

Nếu ∆ < 0 thì , phương trình
vô nghiệm
có nghiệm kép
……………..
(2)
……………..
(3)
……………..
(4)
…………
(8)
……………..
(9)
……………..
(11)
4(b’
2
– ac)
(2b’)
2
– 4ac =
4b’
2
– 4ac =
b' '
a
− + ∆

……………..
(1)
……………..
(5)
…………
(10)
Δ’ = 0
…………
(6)

§5. Công thức nghiệm thu gọn


2. Áp dụng.
Ví dụ 1:
Giải phương trình 5x
2
+ 4x – 1 = 0
bằng cách điền vào chỗ . . . trong các
chỗ sau :
a = . . . c = . . . .
b’ = . . .
5
2
-1
;
;
Δ’ = . . . b’
2
- ac =2

2
– 5.(-1)= 4 + 5 = 9
Δ' .......=
Nghiệm của phương trình :
x
1
=
x
2
=
b'Δ' 2 3 1
a 5 5
− + − +
= =
b'Δ' 2 3
1
a 5
− − − −
= = −
Ta có :
Ta có :
1. Công thức nghiệm thu gọn.
b' '
a
− + ∆
x
1
=
b' '
a

− − ∆
x
2
=
Nếu ∆’ > 0 thì phương trình có hai nghiệm phân biệt :
 Nếu ∆’ = 0 thì phương trình có nghiệm kép :
 Nếu ∆’ < 0 thì phương trình vô nghiệm.
x
1
= x
2
=
b'
a
−
;
Đối với phương trình ax
2
+ bx + c = 0 (a ≠ 0)
và b = 2b’, Δ’ = b’
2
– ac :
Ví dụ 2 : Giải các phương trình sau:
a) 3x
2
+ 8x + 4 = 0
2
7x 4 3x 2 0+ + =
c)
2

x 6 2x 18 0− + =
b)
9
=3>0