Đề cương bài giảng ứng dụng máy tính trong thiết kế tính toán ô tô

TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT HƯNG YÊN
KHOA CƠ KHÍ ĐỘNG LỰC

BÀI GIẢNG
HỌC PHẦN: ỨNG DỤNG MÁY TÍNH TRONG TÍNH
TOÁN THIẾT KẾ Ô TÔ
SỐ TÍN CHỈ: 02
LOẠI HÌNH ĐÀO TẠO: ĐẠI HỌC CHÍNH QUY
NGÀNH: CÔNG NGHỆ KỸ THUẬT Ô TÔ

Hưng Yên - 2015


Lời nói đầu :
Môn ứng dụng Matlap trong kỹ thuật ô tô đ-ợc biên soạn nhằm giúp các bạn
là sinh viên các ngành khoa học kỹ thuật nắm đựoc cơ sở của phần mềm trợ giúp
tính toán Matlap ,qua đó dùng Matlap để giải quyết các bài tập lớn ,đồ án ,luận văn
tốt nghiệp .Matlap thực sự là một phần mềm rất mạnh ,vừa có khả năng lập trình
nh- nhiều ngôn ngữ khác ,vừa là một môi tr-ờng tính toán thực dụng có thể dùng
ngay hàng trăm hàm và ch-ơng trình con đã đ-ợc lập trình sẵn để giải quyết bài
toán về ma trận ,đại số tuyến tính ,giải tích số ,ph-ơng trình vi phân ,quy hoạch
tuyến tính tối -u hoá cũng nh- các ch-ơng trình về đồ hoạ .Hiện nay Matlap đã
xâm nhập vào hầu hết các lĩnh vực ,từ kỹ thuật cơ sở đến những vấn đề có tính
chuyên môn rất cao .
Một -u điểm của Matlap là học là học tập phần mềm này rất đơn giản ,chỉ cần
vài buổi học là học viên có thể nắm đ-ợc phần cơ bản của ch-ơng trình để rồi qua
đó tìm hiểu thêm các tài liệu rất phong phú của Matlap trên mạng internet .Đối với
các bạn đã thành thạo một ngôn ngữ truyền thống nào đó ,việc tham khảo phần
mềm Matlap sẽ giúp cho bạn cơ hội tham khảo rất nhiều ch-ơng trình tính toán tinh
vi của Matlap qua các tập tin nguồn có sẵn ,dựa vào đây bạn có thể viết lại ngôn
ngữ mà bạn -a thích .

Thiết kế bài giảng :
Thac sĩ : Lê Anh Vũ
Thạc sỹ : Đồng Minh Tuấn

1


Ch-ơngI: gii thiệu chung về Matlap, phạm vi ứng dụng
1.1.Giới thiệu chung về matlap
Matlap vừa là ngôn ngữ lập trình vừa là một phần mềm ứng dụng tính toán rất
hiệu quả .Matlap là từ viết tắt của Matrix Laboratory được phát triển bởi tập đoàn
The Math Works,Ins .of Natick,Massachusetts Hoa kỳ từ những năm 1970.Lúc
đầu Matlap đ-ợc dùng chủ yếu để giải quyết các vấn đề về matrân ,đại số tuyến
tính ,giải tích số, hiện nay khả năng tính toán của Matlap rất lớn ,bao trùm nhiều
lĩnh vực khác nhau .
Matlap 6.0 đ-ợc phát hành vào mùa thu năm 2000 và chạy trên nhiều hệ điều
hành khác nhau tiếp đó là phiên bản 6.5 rồi 7.0 và hiên nay là 7.5 .Tr-ơng trình
Matlap bao gồm phần lõi (core) và các Modul phần mềm đ-ợc gọi là các toolbox
(hộp công cụ) . Mỗi toolbox phục vụ những tính toán riêng biệt nào đó ,Ví dụ
toolbox optimization thì chuyên để giải quyết các bài toán tối -u .và vv
1.1.1.cách cài đặt Matlap
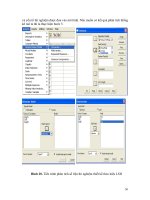
ở đây chúng tôi giới thiệu cho các bạn cách cài đặt Matlap 7.5. đầu tiên các bạn
có thể chọn mua đĩa Matlap phiên bản 7.5 tại các cửa hiệu máy tính .Sau đó cho đĩa
vào ổ CD rom .Sau đó mở dĩa CD vào setup màn hình hien ra nhu sau:

Chọn install,sau đó bấm next một màn hình sau hiện ra :

2

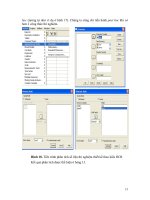
NhËp m· sè vµo password vµ bÊm next

Mét mµn h×nh míi hiÖn ra:

Chän yes vµ bÊm next mµn h×nh sau sÏ hiÖn ra:

3


Chọn Typical và tiếp tục bấm next

Chọn ổ C làm nơi cài ch-ơng trình Matlap bấm next .Nh- vậy Matlap sẽ tự động
cài ch-ơng trình vào máy của bạn
1.2. Giao diện đồ hoạ, các phím chức năng
1.2.1. Các kiểu biến trong Matlap
Trong Matlap sử dụng các biến cơ bản sau:
a.Biến toàn cục
Muốn truy xuất đ-ợc các biến dùng chung cho ch-ơng trình chính và các tập
tin hàm (đóng vai trò nh- các ch-ơng trình con ) thì phải khai báo biến này là biến
toàn cục bằng dòng lệnh
4


>> Goloball ten_bien1
b.Biến kiểu xâu ký tự (string):
Cú pháp lệnh:
names = Dong Minh Tuan
names =
Dong Minh Tuan
number = 0983744750

number =
983744750
c.Biến symbolic :
Cú pháp lệnh để tạo các đối t-ợng simbolic
>> x=symm(x)
x=
x
Ngoài ra còn dùng lệnh symm để khai báo nhiều biến symbolic một lúc :
>> Symm (x,y,z) : Tạo ba biến symbolic x,y,z
1.2.2. Giao diện đồ hoạ
Matlap gồp có 3 màn hình cơ bản :
Màn hình comand
Màn hình comand Work
Màn hình comand off
1.2.3. Các phím chức năng
: phím enter
5


: phím quay lại
: Dịch chuyển con chuột về bên phải man hình
: Dịch chuyển con chuột về bên trái màn hình
: phím dịch chuyển con chuột xuống d-ới màn hình lệnh
1.3.Các ph-ơng pháp làm việc với Matlap.
1.3.1các lệnh cơ bản .
Các hàm thông dụng:

Sqrpt(x) :
Expe(x)
Log(x) :
Log10(x)
Shin(x) :
Cose(x)
Tang(x)
Coto(x)
Asin(x)
Accos(x)
Actan(x)
Acot(x)
Sninh(x)
Sign(x)


Các hằng đ-ợc định nghĩa tr-ớc trong Matlap(predefined constants).
1
2

3
4
5
6

Biến,hằng
Pi
Ans
Eps
I,j
Inf

ý nghĩa

6


7

NaN

1.3.2.Các lệnh dùng trong không gian màn hình làm việc
Thứ tự
1
2
3
4
5
6
7

8
9
10

Lệnh

Công dụng

Cl
Clear
Clear var1
inpput
Exist
Quit
Who
Whoss
%
Dis

1.4. Quy cách viết dãy lệnh, biểu thức của Matlap
Chế độ t-ơng tác trong cách một chỉ thích hợp với bài toán nhỏ ,đơn giản .Đối
với bài toán đòi hỏi phải sử dụng nhiều lệnh ,một tập lệnh đ-ợc dùng lặp đi lặp lại
hoặc làm việc với các dãy số có số phần tử rất lớn chúng ta cần tạo Script file
1.4.1Tạo và sử dụng Script file
Chúng ta có thể viết và l-u các tr-ơng trình Matlap trong các tập tin có phần đuôi
dạng (.m) đ-ợc gọi là các M file .Matlap dùng hai loại M-file là Cript file (tập tin
lệnh) và funtion file (tập tin hàm ) .Hai loại này khác nhau khi tạo file và sử dụng
Cách tạo :

7

Sau khi vào M- file thì có cửa sổ hiện ra (hình2)

Sau khi soạn xong chúng ta l-u lại tên file (không vào tên đuôi .m ).Tên file tuân
theo quy tắc tên biến trong Matlap ,file này đ-ợc l-u trong th- mục hiện hành
(current directory) th-ờng là th- mục work ,sau khi l-u trở lại màn hình Destop để
chạy ch-ơng trình
Cấu trúc đề nghị của một cript file gồm các phần cơ bản sau:
Phần chú thích (comments section) : viết các dòng chú thích cho tr-ơng
trìnhgồm: tên của ch-ơng trình và các từ khoá mo tả ch-ơng trình ,định
nghĩa các biến đầu vào và đầu ra ,chú ý phải xác định rõ đơn vị đo l-ờng cho
tất cả các biến đầu vào và đầu ra ,tên của từng hàm tự tạo đ-ợc sử dụng trong
ch-ơng trình
1.4.2.Tạo và sử dụng funtion file
Một dạng M- file trong Matlap là function file (tập tin hàm ) đây là hàm do
ng-ời sử dụng tạo ra .Khác với script file tất cả các biến trong tập tin hàm đều có
8


tính chất cục bộ (local) có nghĩa là giá trị các biến này không đ-ợc truy xuất bên
ngoài không gian tập tin hàm do vậy dùng tập tin hàm để tránh việc lặp đi lặp lại
một tập lệnh nào đó
Goloball:
Việc khai báo phải thực hiện ở ch-ơng trình chính và ở các function file có liên
quan .Trong các tập tin hàm thì phải khai báo biến toàn cục ở dòng thực thi đầu tiên
và th-ờng viết hoa .
1.5. Làm việc với các tệp dữ liệu của Matlap
Dòng đầu tiên của một function file đ-ợc gọi là dòng định nghĩa hàm (function
definition line)

Function[output variables]
Nhờ từ khoá function Matlap phân biệt đ-ợc một M_file là function file hoặc
là script file .Tên hàm tự đặt tuân theo tên biến trong Matlap
Các dòng tiếp theo là các dòng chú thích ,các biến đầu vào đầu ra ,các đơn vị
đo l-ờng
1.5.1. Những l-u ý về tập tin hàm :
Function

seqppllot

(ý nghĩa là ng-ời lập muốn vẽ một hình vuông khi biết cạnh của nó )
Trong một ch-ơng trình tính toán dùng Matlap ,nếu không cần truy xuất tất cả
các biến trong một script file nào đó hãy sử dụng một tập tin hàm thay thế script
file này nó sẽ làm cho workspace bớt cồng kềnh và giảm đ-ợc bộ nhớ

ch-ơng ii: xử lý các dữ liệu dạng mảng trên matlap
9


và vác ứng dụng
Một trong những điểm mạnh của Matlap là khả năng sử lý một tập số đ-ợc xắp
xếp theo một thứ tự nào đó (gọi là mảng ) nh- là một biến đơn (single
variable).Khả năng này làm cho ch-ơng trình viết bằng Matlap rất gọn và dễ hiểu
.Do mảng là một đối t-ợng cơ sở của Matlap ,nên việc lắm vững các phép tính về
mảng là một trong các yêu cầu cơ bản khi sử dụng Matlap.
2.1. Các ph-ơng pháp tạo mảng

2.1.1. Mảng một chiều (véc tơ).
a.định nghĩa :
x = (a1a2a3a4 )

Hoặc
x = (a1 a2 a3 a4 )
Mảng y =([7,-3,2,0] )là hoàn toàn khác với mảng x ở trên do thứ tự các phần
tử ở hai mảng là khác nhau .Matlap có thể cộng hai mảng x và y có cùng kích th-ớc
để đ-ợc một mảng mới z cung kích th-ớc chỉ bằng một dòng lệnh z = x+ y
x =(a1a2,a3,a4)
y =(a2,a4,a1,a3)
z = x+ y

b.Mảng có các phần tử cách đều :
>> u = [0: : n].
Cách biểu thị chung nhất mảng trong Matlap là :
mảng =([ p:c )
hay mảng = ( a:b )
c. Mảng kiểu dòng (row array)
10


vÝ dô :
V=
a1 a2 a3 a4 a5 a6
d.M¶ng kiÓu cét (colum array)
vÝ dô:
A=(a1,a2,a3,a4)
A=
a1
a2
a3
a4

2.1.2 .M¶ng hai chiÒu :
Mét m¶ng trong Matlap cã thÓ cã nhiÒu dßng nhiÒu cét mét m¶ng nh- vËy cßn
®-îc gäi lµ mét ma trËn m¶ng hai chiÒu ®-îc thÓ hiÖn [ m, n]

2.1.3 .M¶ng nhiÒu chiÒu .
A(1) =

A (2) =

11


2.1.4.Mảng kiểu ô (cell array)
Cú pháp lệnh:
A1=Nguyen van A
A2=26-4-1984
A3=7,10

Nguyen van A
A=
8

7 10

A=
26-4-1984
A =
5

7

6

2

9

6

8

9

4

2.3. Các phép tính thực hiện trên mảng
Matlap có các phép tính về mảng (array operations) còn gọi là phép tính trên các
phần tử t-ơng ứng và các phép tính về matran (matrix operations).
2.3.1.Các phép tính mảng
a.Cộng hai mảng .
ví dụ :
u=(1.....4)
v=(5.....8)

12


r=u+v
r=
6

8 10 12

b.Phép trừ hai mảng:
u=(1......4)
v=(5......8)
r=u-v
r=
-4 -4 -4 -4

c. Phép nhân hai mảng.
Đây là một phép tính đặc biệt trong Matlap dùng toán tử
ví dụ :
u=(5......10)
v=[6.......3)
A=u.v
A=
30 49 72 18 30
ví dụ:
A=(1.......7);
B=(1......6);
C=A.B
C=
12 136 35 48
13


0 21

25 42

d.Phép chia hai mảng:
Giả sử có matran A và matran B có cùng kích th-ớc phép chia C =A: B sẽ đ-ợc
matran có cùng kích th-ớc và
.
ví dụ :
A =(19)
B=(3.4);
C=A: B
C=
0.0313 2.0000 1.0000 0.7500
0.2000 0.4000 0.3478 0.3750

2.3.2.Các phép tính trong Matran

a.Cộng và trừ hai matran
Cho hai matran A= [aij] ,B =[bij] có cùng kích th-ớc ,phép cộng C =A + B hoặc
phép trừ D = A - B sẽ đ-ợc thực hiện nh- cộng hay trừ hai mảng nh- đã trình bày
ở mục trên .Ta có
,

b.Phép nhân hai matran :
Cho matran A có kích th-ớc m p và matran B có kích th-ớc p q tích của
hai matran đ-ợc Matlap thực hiện bằng lệnh A*B và sẽ sinh ra một matran C có
kích th-ớc m q và
với i = 1,2,m và j = 1,2,q
Phép nhân hai matran A và B đòi hỏi matran A và B phải t-ơng thích với nhau
,nghĩa là số dòng của matran B phải bằng số cột của matran A .
c.Chuyển vị hai ma trận :

14


Giả sử có ma trận A =

thì ma tran chuyển vị sẽ là : A =

Cú pháp lệnh:
A=
A...
e.Tính định thức của ma tran vuông
Để tính định thức của matran vuông trong Matlap sử dụng lệnh doet ()
Cú pháp lệnh:
A=
doet[A]
f. Tính ma tran nghịch đảo ;
Để tính matran nghịch đảo dùng lệnh inver
Cú pháp lệnh
A=
inver
g.Tính hạng của một matran
Trong Matlap để tính hạng của một matran nào đó dùng lệnh rak()
Cú pháp lệnh
>> A =
>> rak
p.Rút gọn matran thành dạng bậc thang theo dòng
15


Cú pháp lệnh

>> A =
>> ef
q.Truy xuất một phần tử của ma tran .Trích véc tơ dòng cột matran con.
Khi tạo xong matran A nào đó ,phát hiện phần tử ở dòng n cột m cần thay đổi
giá trị giả sử a thành b ta chỉ việc vào lệnh :
A(n,m) = b
Giả sử có matran A nh- sau:
A=
[ a1, a2, a3, a4]
[ a21, a22, a23, a24]
[ a31, a32, a33, a34]
[ a41, a42, a43, a44]
k.Một số lệnh thông dụng khác trong matran
eig(X) :dùng để tính trị riêng và véc tơ riêng của một matran vuông
[V,D] =eig(X) trả về matran đ-ờng chéo D chứa các trị riêng và một matran V
có các cột là véc tơ riêng t-ơng ứng sao cho : X*V =V*D
[V,D]=eigs(X) trả về một mảtận đ-ờng chéo D chứa sáu trị riêng có giá trị (độ
lớn lớn nhất và một matran V có các cột là các véc tơ riêng t-ơng ứng .Tr-ờng hợp
muốn kết quả có n trị riêng ta dùng eigs(X,n).
lu(X) dùng để phân tích matran vuông thành các matran đặc biệt
[L,U] = lu (X) tạo matran tam giác trên U và một matran L (là tích của một
matran tam giác d-ới và một matran hoán vị )sao cho X = L*U

16


[L,U,P] = lu(X) tạo matran tam giác d-ới L ,matran tam giác trên U và matran
hoán vị sao cho : P*X = L*U .Ta có quam hệ A-1 = U-1L-1P
sparse (X) :Chuyển matran X thành thành matran sparese (matran th-a)
full(X) chuyển matran sparse (X) thành Matran đầy đủ .

issparse (X) trả về giá trị 1 nếu matran X là matran sparse và trả về giá trị 0
nếu matran X không phải là matran sparse

Bài tập cuối ch-ơng
câu 1 : Thiết lập matran vuông A có kích th-ớc 10

10 nh- sau bằng ba cách:

Câu 2 : Tự tạo một cơ sở dữ liệu của các học viên cùng lớp với các tr-ờng :
ho_ten,email,dia_chi,số điện thoại
Câu3.Tính độ cứng của nhíp :

Trong đó

là hệ số thực nghiệm ,

,E là mô dul đàn hồi của vật liệu .

với lk là ẵ chiều dài lá nhíp thứ k (tính từ quang treo đến đầu mút
của lá )
Dữ liệu đã biết
chỉ số của lá

Bề rộng b,Cm

Bề dầy lá nhíp Mô men quán tính
h,Cm
J Cm4

1-6

45

0.70

4.5*0.703/12
=0.128

17


7-9

45

4.5*0.5753/12
=0.0713

0.575

Một phần hai chiều dài lá nhíp (tính từ quang treo đến đầu mút của lá )
L1

L2

L3

L4

L5

L6

L7

L8

L9

68.5

67.2

57.6

50.4

43.0

35.0

28.0

20.6

13.0

Tr-ơng trình tính độ cứng của nhíp trong Matlap
%%Nhap du lieu
h(1)=0.7;h(2)=0.7;h(3)=0.7;h(4)=0.7;h(5)=0.7;h(6)=0.7;

h(7)=0.575;h(8)=0.575;h(9)=0.575
l(1)=50;l(2)=48.5;l(3)=37.5;l(4)=28.0;l(5)=20.0;l(6)=13.0;
b=4.5;a1=0.85 E= 21*10^5
%%tinh toan cac dac tinh hinh hoc la nhip
jk=b*h.^3/12;jk=cumsum(jk)
yk=1./jk;yk(10)=0;Dyk=-diff(yk);
a=l(1)*ones(1,10)-l;a=a(2:10);
%%Tinh do cung cua nhip
C=a1*6*E/sum(a.^3.*Dyk)

Câu 4.Tính toán bền các lá nhíp .
Phản lực tác động tại các đầu mút của lá nhíp đ-ợc xác định từ hệ ph-ơng trình :

Trong đó Ak,Bk,Ck ,đ-ợc xác định từ biểu thức :
,

,

Trong đó lk là 1/2 chiều dài lá nhíp thứ k (tính từ quang đến đầu mút của lá ).
Jk là mô men quán tính mặt cắt ngang của lá nhíp thứ k :
Cho dữ liệu các lá nhíp và tải trọng :
Số hiệu lá 1
nhíp

2

3

4

5

6

Chiều dày 0.7

0.7

0.8

0.8

0.8

0.8
18


lá nhíp
Bề rộng lá 6.5
nhíp

6.5

6.5

6.5

6.5

6.5

Nửa chiều 50.0
dài lá nhíp

48.5

37.5

28.0

20.0

13.0

Khoảng cách giữa bulông ngàm nhíp :12 cm
Tải trọng đặt lên nhíp 900 Kg
%%Nhap du lieu
h=0.8*ones(1,6);h(1)=0.7;h(2)=0.7;b=6.6;Q=900;d=12;
l(1)=50;l(2)=48.5;l(3)=37.5;l(4)=28.0;l(5)=20.0;l(6)=13.0;
%%Tinh cac he so
jk=b*h.^3/12;jk1=jk(2:6);jk=jk(1:5);
Lk=L(1:5);Lk1=L(2:6);
A=0.5*jk1./jk.*(3*Lk./Lk1-ones(1,5));
p=zeos(5,1);p(1)=-Q/2*A(1);
Ak=A(2:5);Ck=C(1:4);
%%Thiet lap matran he so
M=diag(Ak,-1)+diag(Bk)+diag(Ck,1);
%%Tinh cac phan luc
X=inv(M)*p

19


Ch-ơng III : Công cụ toán học,Cách lập trình ứng dụng
trong Matlap
3.1. Các cộng cụ xử lý đa thức.
3.1.1. Giải ph-ơng trình đại số :
Để giải ph-ơng trình đại số siêu việt dùng lệnh solve
Cú pháp lệnh :
f(x) = a1xn +a2xn-1 + anx + a0
% giải ph-ơng trình đại số siêu việt ;
Solvel
Cú pháp lệnh :
a1xn +a2xn-1 + anx + a0 = 0 % giải ph-ơng trình đại số siêu việt ;
solvel
Nếu trong ph-ơng trình hoặc biểu thức có nhiều hơn một biến. Matlap sẽ giả
thiết biến gần với biến mặc định x (theo bảng chữ cái ) là biến phải tìm (ẩn của bài
toán ).
Cú pháp lệnh :
a1x +a2y + anz + a0 = 0
solvel
ví dụ : Giải ph-ơng trình đại số 6x2 +5x -8 =0
6.x^2 + 5.x - 8=0
Solvelk
ans =
.81090998855468627988128121586250
-1.6442433218880196132146145491958
20

3.1.2 .Giải hệ ph-ơng trình
Để giải hệ ph-ơng trình thì chúng ta cũng dùng hàm solvel
Cú pháp lệnh:
f(x1) = a1xn +a2xn-1 + anx + a0;
f(x2) = b1xn +b2xn-1 + bnx + b0;
h = solvel
3.2.Tối -u hoá các hàm số :
3.2.1. Tìm cực trị hàm số
a.Hàm fminbnb
Dùng để tìm điểm cực tiểu của một hàm một biến trong một khoảng định
tr-ớc .Điểm cực tiểu của hàm một biến y = fun(x) trong khoảng định tr-ớc (x1,x2 )
đ-ợc xác định bằng hàm fminbnb theo cú pháp :
fminbnb
Trong đó fun là tên của hàm cần tìm cực tiểu (ở dạng inline object hay dạng m
file ) . x và fval đ-ợc trả về giá trị của biến x thuộc (x1,x2 ) tại đó hàm fun đạt giá
trị cực tiểu
b.Hàm fminunc
Hàm fminunc dùng để tìm điểm cực tiểu địa ph-ơng của một hàm nhiều biến
từ một điểm định tr-ớc ,nó đ-ợc dùng để giải bài toán tối -u không có điều kiện
dàng buộc .
cú pháp :
fminunc
Trong đó fun là tên của hàm cần tìm cực tiểu (ở dạng inline object hay dạng m
file ) , x và fval đ-ợc trả về là giá trị của biến x ở lân cận điểm x0 mà tại đó hàm
fun đạt cực tiểu ,x0 là điểm định tr-ớc và Matlap bắt đầu dò tìm điểm cực tiểu từ
điểm đó .
21

c. Hàm fmincon
Hàm fmincon dùng để tìm cực tiểu của một hàm với các điều kiện dàng buộc
.Vấn đề ở đây là tìm cực tiểu của hàm fun(x) với các điều kiện dàng buộc :

Trong đó:
x,b,beq,lb,ub là các véc tơ
A,Aeq : là các ma tran
C(x), ceq(x) là hàm phi tuyến trả về véc tơ ,fun(x) là hàm trả về trị vô h-ớng
Cú pháp lệnh :
>> [x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Trong đó x và fval đ-ợc trả về giá trị của biến x mà tại đó hàm fun đạt cực tiểu
,fun là tên hàm cần tìm cực tiểu (ở dạng m file) ,x0 là điểm định tr-ớc và Matlap
bắt đầu dò tìm cực tiểu từ điểm đó .A,b,Aeq,lb,ub là các véc tơ và ma tran xác định
các điều kiện ràng buộc, nonlcon là tên hàm dạng m file định nghĩa các hàm ở vế
trái của các điều kiện dàng buộc
3.2.2 .Ph-ơng pháp nội suy trong Matlap
a.Nội suy một chiều :
cú pháp lệnh của nội suy tuyến tính :
>> y = interp
Trong đó :

22


- y là véc tơ chứa các giá trị nội suy tại các giá trị t-ơng ứng xác định bởi véc
tơ x*
- Y là véc tơ chứa các giá trị đ-ợc biết tr-ớc của hàm tại các giá trị t-ơng ứng
xác định bởi véc tơ x
b.Nội suy hai chiều
cú pháp lệnh

>> Z = interp
ứng với mỗi đa thức nội suy,Matlap có thể xác định và hiển thị véc tơ sai lệch và
độ lớn của các véc tơ sai lệch đó

3.3 Đạo hàm và tích phân các hàm số :
3.3.1. Tính đạo hàm
Để tính đạo hàm của hàm số dùng lệnh diffu.
Tr-ớc tiên khai báo các biến số sau đó dùng lệnh diffu để tính đạo hàm của nó
Cú pháp lệnh :
diffu
Trong đó x là biến số của hàm n là bậc mũ của biểu thức ,p là cấp của đạo hàm
cần tính . Nếu trong biểu thức tính toán có từ hai biến trở lên để tính đạo hàm riêng
của biểu thức theo biến nào đó ta dùng
Cú pháp lệnh nh- sau :
f(x,y..z) = a*x + b* y + ..c*z
diffu
% tính đạo hàm riêng bậc p theo biến nào đấy
ví dụ: Tính đạo hàm riêng cấp hai theo biến y của hàm số f(x,y) = ax3 + by4 + 9
diffu
23


ans =
12*b*y^2
3.3.2. Tính tích phân hàm số
Matlap đã cho ra một số lệnh để tính tích phân của hàm số nh-ng thông dụng và
dễ dùng thì th-ờng hay dùng lệnh intd
Đối với tích phân không xác định:
Cú pháp lệnh :
intd %Tính tích phân

ans = ..
Đối với tích phân xác định
Cú pháp lệnh :
intd
Trong đó f(x) là hàm số tính tích phân ,a và b lần l-ợt là các cận trên và cận d-ới
của tích phân
3.3.3. Khai triển Taylor một hàm
Hàm taylor (f,n,a) khai triển Taylor hàm số f thành một đa thức symbolic xấp
xỉ bậc (n-1) tại lân cận điểm a ,nếu a đ-ợc bỏ qua xem nh- a = 0 thì chúng ta có
khai triển (Maclaurin) .
Cú pháp lệnh :
f(x) = a1xn +a2xn-1 + anx + a0;
taylork
3.3.4. Tính các tổng số hữu hạn
Giả sử cần tính tổng các số hữu hận mà ta đã biết tr-ớc kết quả trong Matlap
dùng lệnh symskjum:

24