BÀI GIẢNG ỨNG DỤNG TIN HỌC TRONG THIẾT KẾ THÍ NGHIỆM VÀ XỬ LÝ SỐ LIỆU (Phương pháp nghiên cứu nâng cao) part 8 pdf

36
và yếu tố thí nghiệm được đưa vào mô hình. Nếu muốn có kết quả phân tích thống
kê mô tả thì ta thực hiện bước 5.





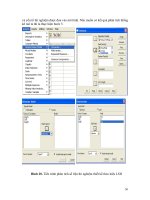
Hình 20. Tiến trình phân tích số liệu thí nghiệm thiết kế theo kiểu LSD


37
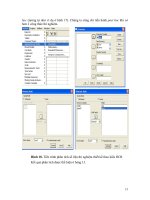
• Bước 4 : Khai báo mô hình phân tích (hình 18). Căn cứ vào mô hình
phân tích để khai báo mô hình. Nếu muốn xem ảnh hưởng đơn lẻ thì ta chọn từng
biến một. Nếu muốn xem ảnh hưởng của tương tác của các biến thì ta chọn đồng
thời các biến. Nếu chúng ta không thực hiện bước này thì máy tính sẽ thực hiện
theo chế độ mặc định. Chế độ mặc định là mô hình phân tích đầy đủ, có nghĩa bao
gồm cả
ảnh hưởng đơn lẻ và ảnh hưởng tương tác. Trong ví dụ này chúng ta chỉ
chọn mô hình gồm ảnh hưởng của nhân tố chính : nhân tố hàng, nhân tố cột, và
nhân tố giống. Trong ví dụ này chúng ta không thể đưa tương tác vào mô hình.
Nếu đưa tương tác vào thì chúng ta sẽ có các mối tương tác sau đây : hàng x cột ;
hàng x giống ; cột x giống ; và hàng x cột x giống. Lý do không thể đưa tương tác
vào mô hình vì chúng ta không có đầy đủ độ tự do cho phân tích phương sai.
• Bước 5: Vào trình
ứng dụng thống kê mô tả trong option (hoàn toàn
giống như ví dụ ở hình 16.)
• Bước 6 : Nếu kết quả bác bỏ giả thuyết H
0
và chấp nhận H

A
thì
chúng ta phải tiến hành phân tích post hoc. Nếu ta chấp nhận H
0
, thì chúng ta
không cần thực hiện post hoc (tương tự như ví dụ ở hình 17). Chúng ta cũng chỉ
tiến hành post hoc khi có hơn 2 công thức thí nghiệm.
Kết quả phân tích được thể hiện ở bảng 17. Cách diễn giải kết quả hoàn
toàn tương tự như ví dụ phân tích kết quả thiết kế thí nghiệm theo kiểu CRD và
RCB. Qua bảng 17 ta thấy rằng các giống khác nhau tạo nên năng suất khác nhau
(P <0,05).
Bảng 17. Kết qu
ả phân tích số liệu thí nghiệm thiết kế theo kiểu LSD

Dependent Variable: Năng suất
Source
Sum of
Squares df
Mean
Square F Sig.
Corrected Model 1,285(a) 9 ,143 6,898 ,014
Intercept 28,481 1 28,481 1375,962 ,000
Hàng ,030 3 ,010 ,485 ,705
Cột ,818 3 ,273 13,178 ,005
Giống ,437 3 ,146 7,030 ,022
Error ,124 6 ,021
Total 29,890 16
Corrected Total 1,409 15
R
2

= ,912 (R
2
điều chỉnh = ,780)

Kết quả ở bảng 17 không chỉ ra được giống nào có năng suất khác với
giống nào do vậy cần phải phân tích post hoc để kiểm tra sự sai khác theo cặp. Bản
chất của kiểm tra này là phép kiểm tra t. Qua kết quả ở bảng 18 ta thấy rằng giống
C có năng suất thấp hơn tất cả các giống còn lại (P <0,05) và không có sự khác
biệt về năng suất giữa giống ngô A, B và D (P >0,05).

38
Bảng 18. Kết quả phân tích post hoc về ảnh hưởng của các giống ngô đến
năng suất ngô
Đa so sánh (Multiple Comparisons)
Biến phụ thuộc (Dependent Variable): Năng suất
LSD
(I)
Giống
(J)
Giống
Mean
Difference
(I-J) Std. Error Sig. 95% Confidence Interval

Lower
Bound
Upper
Bound
A B -0,01 0,10 0,94 -0,26 0,24
C 0,40 0,10 0,01 0,15 0,65

D 0,13 0,10 0,27 -0,12 0,37
B A 0,01 0,10 0,94 -0,24 0,26
C 0,41 0,10 0,01 0,16 0,66
D 0,13 0,10 0,24 -0,12 0,38
C A -0,40 0,10 0,01 -0,65 -0,15
B -0,41 0,10 0,01 -0,66 -0,16
D -0,28 0,10 0,04 -0,52 -0,03
D A -0,13 0,10 0,27 -0,37 0,12
B -0,13 0,10 0,24 -0,38 0,12
C 0,28 0,10 0,04 0,03 0,52

Như đề cập ở trên rong mô hình phân tích số liệu của thí nghiệm thiết kế theo
kiểu LSD phải luôn luôn bao gồm cả yếu tố bị khống chế. Tuy nhiên, chúng ta
không quan tâm đến ảnh hưởng của yếu tố bị khống chế (yếu tố hàng và yếu tố
cột) đến biến phụ thuộc. Một số phần mềm tin học thậm chí không đưa kết quả về
mứ
c ý nghĩa (giá trị P) của ảnh hưởng của yếu tố hàng và yếu tố cột. Bảng 19 trình
bày kết quả phân tích số liệu theo kiểu LSD bằng phần mềm GENSTAT.
Bảng 19. Kết quả phân tích ANOVA về ảnh hưởng của các giống ngô đến
năng suất ngô bằng phần mềm GENSTAT
Variate: Năng suất

Source of variation (N. Biến động) d.f. s.s. m.s. v.r. F pr.

Hàng stratum 3 0,03014 0,01005 0,49

Cột stratum 3 0,81832 0,27277 13,18
Hàng.Cột stratum
Giống 3 0,43654 0,14551 7,03 0,022
Residual (hiệu dư) 6 0,12419 0,02070

Total (tổng) 15 1.40920

39
Tóm lại, phân tích ANOVA cho các kiểu thiết kế thí nghiệm có sự khống
chế ban đầu, về mặt cơ bản giống với phân tích ANOVA cho kiểu thiết kế thí
nghiệm CRD. Điểm mẫu chốt là xem xét các yếu tố cần được khống chế (yếu tố
khối trong RCB, yếu tố hàng và cột trong LSD) như là yếu tố thí nghiệm và chú ý
khai báo mô hình phân tích một cách hợp lý.

BÀI 6. ÁP DỤNG QUY TẮC NGẪU NHIÊN TRONG THIẾT KẾ THÍ
NGHIỆ
M VỚI MỘT NHÂN TỐ
Ba đặc tính quan trọng của bất kỳ một thí nghiệm nào là: (i) tính lặp lại (ii)
tính ngẫu nhiên và (iii) khống chế sự sai khác ban đầu. Tính ngẫu nhiên ở đây có
nghĩa là các đơn vị thí nghiệm nhận các nghiệm thức hoặc các nghiệm thức được
phân chia vào các đơn vị thí nghiệm một cách ngẫu nhiên. Về cơ bản ta có thể nói
rằng việc áp dụng tính ngẫu nhiên hoàn toàn giống nhau trong các kiểu thiết kế
thí
nghiệm khác nhau. Điểm mấu chốt là áp dụng tính ngẫu nhiên ở nơi nào và đối
tượng nào. Trong thiết kế thí nghiệm CRD một nhân tố, tính ngẫu nhiên được áp
dụng cùng lúc trên tất cả đơn vị thí nghiệm. Trong thiết kế thí nghiệm RCB, tính
ngẫu nhiên được áp dụng trong mỗi khối. Ví dụ nếu chúng có 5 khối thì quá trình
ngẫu nhiên hóa phải được thực hiện 5 lần. Mỗi lần cho mỗi khối. Trong thiết kế thí
nghi
ệm kiểu LSD quá trình ngẫu nhiên hóa bắt đầu từ chọn hình vuông la tinh
chuẩn, sau đó ngẫu nhiên hóa trật tự của hàng và cuối cùng là ngẫu nhiên hóa trật
tự của cột.

Chúng ta có thể thực hiện quá trình ngẫu nhiên bằng cách bốc thăm, bóc bài

hay sử dụng các bảng số ngẫu nhiên. Trong nội dung của phần này chúng tôi giới
thiệu kỹ thuật ngẫu nhiên hóa bằng cách dùng hàm RAND() trong EXCEL.

6.1. Ngẫu nhiên hóa trong thiết kế thí nghiệm kiểu CRD và RCB
Như
đã nói ở trên, quá trình ngẫu nhiên hóa trong hai kiểu thiết kế thí
nghiệm này hoàn toàn giống nhau. Trong thiết kế RCB, số lần thực hiện ngẫu
nhiên hóa bằng số khối. Ở đây, chúng tôi chỉ lấy một ví dụ về quá trình ngẫu nhiên
hóa trong thiết kế thí nghiệm CRD.

Ví dụ 17. Một nhóm nghiên cứu quan tâm đến ảnh hưởng của 3 chất kích
thích sinh trưởng CT1, CT2 và CT3 đến sinh trưởng của một loại cây trồng A. Thí
nghiệm đượ
c tiến hành trong nhà kính. Có 24 đơn vị thí nghiệm, mỗi đơn vị là một
chậu. Thí nghiệm được thiết kế theo kiểu CRD. Hảy phân chia các đơn vị thí
nghiệm vào các nghiệm thức hoặc ngược lại các nghiệm thức vào các đơn vị thí
nghiệm.
• Bước 1 (B1): Lập danh sách các chậu thí nghiệm và đánh số các
chậu theo thứ tự từ 1-24

40
• Bước 2 (B2): Gán cho mỗi chậu một số ngẫu nhiên bằng cách sử
dụng hàm RAND(). Hàm RAND() cho phép tạo ra các số ngẫu nhiên có giá trị
trong khoảng [0-1]. Chúng ta có thể tạo ra các số ngẫu nhiên trong một khoảng giá
trị nào đó bằng cách sử dụng hàm RANDBEETWEEN(giá trị 1; giá trị 2). Điều
cần đặc biệt quan tâm là kết quả hàm RAND() luôn luôn thay đổi do vậy chúng ta
phải cố định các giá trị ngẫu nhiên ngay sau khi đã tạo ra. Quá trình cố định này có
thể
thực hiện thông qua trình ứng dụng past special - past value (hình 20). Cần
paste các giá trị ngẫu nhiên vừa tạo ra trên chính các giá trị vừa tạo ra. Mục đích là

chuyển từ dạng formula thành dạng value.

Bảng 20. Quá trình ngẫu nhiên hóa trong thiết kế thí nghiệm kiểu CRD

B1 B2 B3 B4
Chậu thí
nghiệm
Số ngẫu
nhiên
Chất sinh
trưởng
Chậu thí
nghiệm
Số ngẫu
nhiên
Chất sinh
trưởng
1 0,485241372 CT1 1 0,033928302 CT2
2 0,83296448 CT2 2 0,035714957 CT1
3 0,755481259 CT3 3 0,049174649 CT3
4 0,792772895 CT1 4 0,061979632 CT3
5 0,033928302 CT2 5 0,105024436 CT3
6 0,421183444 CT3 6 0,15555833 CT1
7 0,653933273 CT1 7 0,421183444 CT3
8 0,490003494 CT2 8 0,448307137 CT3
9 0,535638176 CT3 9 0,485241372 CT1
10 0,713850843 CT1 10 0,490003494 CT2
11 0,940457894 CT2 11 0,535638176 CT3
12 0,448307137 CT3 12 0,643343235 CT3
13 0,035714957 CT1 13 0,653933273 CT1

14 0,967915049 CT2 14 0,656308708 CT1
15 0,105024436 CT3 15 0,663214746 CT2
16 0,656308708 CT1 16 0,713850843 CT1
17 0,819146507 CT2 17 0,755481259 CT3
18 0,049174649 CT3 18 0,792772895 CT1
19 0,15555833 CT1 19 0,819146507 CT2
20 0,949684416 CT2 20 0,83296448 CT2
21 0,061979632 CT3 21 0,913293136 CT1
22 0,913293136 CT1 22 0,940457894 CT2
23 0,663214746 CT2 23 0,949684416 CT2
24 0,643343235 CT3 24 0,967915049 CT2

• Bước 3 (B3): Gán các công thức thí nghiệm vào các chậu theo thứ tự
từ CT1 đến CT3 (Bảng 20)