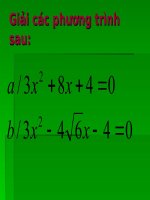công thức nghiệm thu gọn Đ số 9 tiết 55

Chào mừng quý thầy
cô giáo về dự giờ

Kim tra bi c
Nờu công thức nghiệm ca phng trỡnh bc 2:
Đối với phương trình ax
2
+ bx + c = 0 ( a 0 ) và biệt thức = b
2
- 4ac:

Nếu > 0 thì phương trình bậc hai có hai nghiệm phân biệt:
x
1
= ; x
2
=

Nếu = 0 thì phương trình có nghiệm kép x
1
= x
2
=

Nếu < 0 thì phương trình vô nghiệm.
b
2a
+
b
2a

b
2a

Giải phương trình bằng cách dùng công thức nghiệm :
a)3x
2
+ 8x + 4 = 0
b)
02267
2
=+ xx

Giải
a) 3x
2
+ 8x + 4 = 0
2
8 4.3.4 64 48 16 0;
∆= − = − = >
4
∆ =
Ph­¬ng tr×nh cã hai nghiÖm ph©n biÖt :
1 2
8 4 4 2 8 4 12
; 2
2.3 6 3 2.3 6
x x
− + − − − − −
= = = = = = −

( )
4;0
1656722.7.426
2
=∆>∆
=−=−−=∆
Pt có 2 nghiệm phân biệt
7
223
7.2
426
;
7
223
7.2
426
21
−
=
−
=
+
=
+
=
xx
b) 7x
2
- 6 x + 2 = 0
2

2
b ac
′ ′
∆ = −
Tiết 55:

Cho phöông trình ax
2
+bx + c = 0 (a≠0)
Nếu đặtù b = 2b’
1. Công thức nghiệm thu gọn
Kí hi u ệ
2
b ac
′ ′
∆ = −
4
′
∆ = ∆
∆
Töø ñoù ta coù
∆
∆
Nhận xét về dấu của và ’ từ đó suy ra số nghiệm
của phương trình và tính số nghiệm của phương trình
theo ’ và b’
( )
'2
∆=∆

∆
Hãy tính biệt thức theo b’?
( )
( )
acbacbacbacb −=−=−=−=∆
22
2
2
'44'44'24

1
2
b
x
a
− + ∆
= =
a
b
2
'2'2 ∆+−
a
...
=
............
...........
2
............
2
2

==
∆−−
=
aa
b
x
Nếu ’ >0 thì ... ... phương trình có ....
∆∆
Hoạt động nhóm. Điền vào dấu ( .... ) để hoàn thành các khẳng
định sau
Nếu ’ = 0 thì ........ Phương trình có .........
∆
∆
aa
b
xx
........
.......
.......
2
21
==
−
==
Nếu ’ < 0 thì ......... Phương trình ...............
∆
∆
> 0
2 nghiệm phân biệt
a

b
'
' ∆+−
a
b
2
2'2
'
∆−−
a
b
'
'
∆−−
= 0
nghiệm kép
a
b
2
'2
−
a
b'
−
< 0 vô nghiệm