Luyện tập: Ứng dụng tích phân tính diện tích hình phẳng

Ngày soạn : Ngày dạy :
Tiết : 63
BÀI TẬP
1.Mục tiêu :
* Về kiến thức : Giúp HS: Nắm vững các dạng thường gặp ứng dụng tích phân để tính
diện tích hình phẳng và các công thức áp dụng cho từng trường hợp cụ thể.
* Kĩ năng: Giúp HS: vận dụng được các công thức nêu trong bài vào việc giải các bài toán
cụ thể.
.* Tư duy thái độ
- Tư duy: lôgic, linh hoạt, độc lập, sáng tạo.
- Thái độ: cẩn thận, chính xác.
2.Chuẩn bị phương tiện dạy học:
- Phương tiện: GV chuẩn bị hình vẽ đồ thị bài tập 27b, c trên bảng phụ.
3.PPDH : gợi mở vấn đáp thông qua các hoạt động điều khiển tư duy và hoạt động nhóm.
4.Tiến trình bài học và các hoạt động
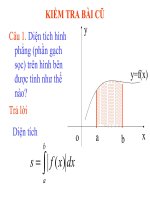
* Kiểm tra bài cũ:
- Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và 2
đt x = a, x = b ?
- Áp dụng: Bài tập28c) (sgk/167)
1.HĐ1: Bài tập 27c (sgk/167)
Hoạt động của HS Hoạt động của GV
- Một HS nêu cách giải và công thức áp dụng.
Giải pt:





<−=
=
=

⇔=−−
02
2
0
022
224
x
x
x
xxx
Diện tích hình phẳng cần tìm là:
15
64
15
64
)4(2)2(
2
2
0
4
2
0
224
=−=
−=−−=
∫∫
dxxxdxxxxS
- Gọi 1 HS nêu cách giải ? và giải bài
toán.
- GV theo dõi và minh hoạ đồ thị (trên

bảng phụ)
2.HĐ2: Bài tập 27b (sgk/167)
Hoạt động của HS Hoạt động của GV
- Một HS giải:
Giải pt:



=
=
⇔=
1
0
3
x
x
xx
12
1
12
1
)(
3
1
0
1
0
3
=−=
−=−=

∫∫
dxxxdxxxS
* Nếu x là hàm của biến y thì ta tính diện tích
hình phẳng giới hạn bởi đồ thị hai hàm số:
x = y
2
, x = y
3
Ta có :
12
1
1
0
32
=−=
∫
dyyyS
-Gọi 1 HS lên nêu cách giải và giải bài
toán.
H1: Nếu coi x là hàm của biến y thì diện
tích hình phẳng trên được tính như thế
nào ?
-GV minh hoạ bằng đồ thị 2 hàm số trên
bảng phụ.
- GV nhận xét và KL.
3.HĐ3: Tính diện tích hình phẳng giới hạn bởi các đường:

2
3
10

xxy
−=
và



>−
≤−
=
)1(,2
)1(,
xx
xx
y
Hoạt động của HS Hoạt động của GV
- HS nhận nhiệm vụ.
- HS vẽ đồ thị, xđ phần hình phẳng, chia
hình phẳng thành 2 phần.
Giải các PT:
2
13
)2()
3
10
(
)()
3
10
(
32

3
10
0
3
10
3
1
2
1
0
2
2
2
=−−−+
−−−=
=⇔−=−
=⇔−=−
∫
∫
dxxx
dxxxxS
xxxx
xxxx
- Các HS khác theo dõi và góp ý.
- Giao bài toán cho HS.
- Yêu cầu HS vẽ đồ thị, xác định phần
hình phẳng cần tìm diện tích, từ đó tìm
cách giải.

- GV nhận xét và KL.

4.HĐ4: Củng cố: các dạng thường gặp tìm diện tích hình phẳng giới hạn bởi đồ thị một số
hàm số.
* BTVN: Tìm diện tích hình phẳng giới hạn bởi:
a) đồ thị hàm số y = sinx trên đoạn
[ ]
ππ
;
−
và trục hoành.
b) trục hoành, trục tung. Parabol (P) : y = x
2
-2x +2 và tiép tuyến với (P) tại điểm M(2 ; 2)
* Rút kinh nghiệm bài giảng: