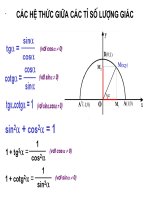
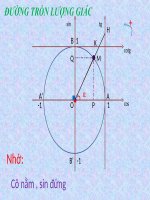
He thuc luong giac co ban

Phần 1: Biến đổi lợng giác
Bài 1. Tính A = sinx.cosx; B = sin
3
x + cos
3
x; C = tanx+cotx; D = tan
2
x+cot
2
x; E = tan
3
x+cot
3
x biết:
a) sinx+cosx = 1/3 b)sinx+cosx = -3/4 c) sinx cosx=4/5 với sinx+cosx<0 d) sinx-cosx = -1/2.
Bài 2. Cho cotx = 2, tính: A = (3sinx+5cosx)/(7sinx-8cosx); B = (8sinx-3cosx)/(sinx+4cosx)
C = (sin
3
x+5cosx)/(7sinx+cos
3
x); D = (6sin
3
x+cos
3
x)/(sinx-cosx); E = (6sinx-5cosx)/(3sin
3
x-23cos
3
x).
Bài 3. Cho 3sin
4

x+cos
4
x=1. Tính A = 4sin
2
x+8cos
2
x B = 7sin
2
x-3cos
2
x.
Bài 4. Cho sin
4
x+2cos
4
x=1. Tính A = sin
2
-9cos
2
x B = 5sin
2
x-6cos
2
x.
I- Chứng minh đẳng thức
1/.
2
1 sin
2
1 2

2
1 sin
x
tg x
x
+
= +

2/.
2 2 4
1 cot 1
.
2 2 2 2
1 cot cot
tg x g x tg x
tg x g x tg x g x
+ +
=
+ +
3/.
1 sin cos
cos 1 sin
a a
a a

=
+

cos 1
1/.

1 sin cos
a
tga
a a
+ =
+

sin 1 cos 2
2 / .
1 cos sin sin
a a
a a a
+
+ =
+
2
cot 1
3 / . . 1
2
cot
1
tga g a
ga
tg a

=


1 cos 1 cos 4cot
4 /.

1 cos 1 cos sin
a a ga
a a a
+
=
+
2 2
5 /.(sin cos ) (sin cos ) 4sin .cosa a a a a a+ + =
6 / .1 2sin .cos sin .cos .(1 ).(1 cot )a a a a tga ga
+ = + +
2 2 2 2
7 / . sin .sintg a a tg a a
=

2
(sin cos ) 1
2
8/. 2
cot sin .cos
a a
tg a
ga a a
+
=

9/.
2 2
sin cos
1 sin cos
1 cot 1

=
+ +
x x
x x
gx tgx
10/.
2 2
sin cos
1 sin cos
1 cot 1
=
+ +
x x
x x
gx tgx
11/. A, sin
4
x-cos
4
x=1-
2cos
2
x B, sin
4
x+cos
4
x=1-2cos
2
x.sin
2

x C, sin
6
x+cos
6
x=1-3sin
2
x.cos
2
x
D, sin
8
+cos
8
x=1-4sin
2
x.cos
2
x+2sin
4
x.cos
4
x 12/. a)sin
2
x-tg
2
x=tg
6
x(cos
2
x-cotg

2
x)b)
3 3
3 3
2 2
1 cot
cot
sin sin .cos cos
+ = +
tg x g x
tg x g x
x x x x

13/. A,
sin
1
3
cos (1 cos )
sin

=
+
tgx x
x x
x
B,
sin cos 1 cos
sin cos 1 1 sin
x x x
x x x

+
=
+ +

II- Rút gọn biểu thứcA=cos
2
x+cos
2
x.tg
2
x
1 1
1 1
cos cos
B tgx tgx
x x

= + + +
ữ ữ


2
2cos 1
sin cos
x
C
x x

=
+

cos sin
2 2
sin 1 cos 1
sin cos
x x
D x x
x x


ữ
ữ


= + + +
E=(tgx+cotgx)
2
-(tgx-cotgx)
2
2 2
sin
2 2
cos cot
x tg x
A
x g x

=


2 2 2

2 2 2
cos cos .cot
sin sin .
x x g x
B
x x tg x
+
=
+
cos
sin cot
tga a
C
a ga
=

2 2 4
2 2 4
sin cos cos
cos sin sin
x x x
N
x x x
+
=
+
cos .cot sin .
1 1
sin cos
a ga a tga

A
a a

=


1 sin 1 sin
1 sin 1 sin
x x
B
x x
+
= +
+
( )
2
1 sin cot 1 cotC x gx gx
= +
III- Chứng minh các biểu thức sau không phụ thuộc x: A=cos
4
x-sin
4
x+2sin
2
x (=1) B=cos
4
x+sin
2
x.cos
2

x+sin
2
x (=1) C=2(cos
6
x+sin
6
x)-3(sin
4
x+cos
4
x) (=-1) D=3(sin
8
x-
cos
8
x)+4(cos
6
x-2sin
6
x)+6sin
4
x (=1)E=
4 2 4 2
sin 4 cos cos 4sinx x x x+ + +
(=3) A=2(sin
4
x+cos
4
x+sin
2

x.cos
2
x)
2
-(sin
8
x+sin
8
x) B=sin
6
x+cos
6
x-2sin
4
x-cos
4
x+sin
2
x
4 4
6 6
sin cos 1
sin cos 1
x x
C
x x
+
=
+
D=(sin

4
x+cos
4
x-1)(tg
2
x+cotg
2
x+2)
2 2
2
cot cos sin .cos
cot
sin
g x x x x
E
gx
x

= +

2 2 2 2
2 2
cos cot cos
sin cos
tg x x g x x
F
x x

= +
2

6
6 2
1 3.
cot cos
tg x
G tg x
g x x
=
H=cos
2
x.cotg
2
x+5cos
2
x-cotg
2
x+4sin
2
x
I=(1+cotgx)sin
3
x+(1+tgx)cos
3
x-sinx-cosx
( ) ( )
2
2
2 2
1
1 1 cos

tg x
K tg x x
tgx


= + +
ữ

M=sin
8
x+cos
8
x+6sin
4
x.cos
4
x+4sin
2
x.cos
2
x(sin
4
x+cos
4
x)
B- Bài tập ứng dụng:
I- Chứng minh đẳng thức
Bài 1.
Chứng minh rằng:
2

1 sin
2
1 2
2
1 sin
x
tg x
x
+
= +

Bài 2.
Chứng minh rằng:
2 2 4
1 cot 1
.
2 2 2 2
1 cot cot
tg x g x tg x
tg x g x tg x g x
+ +
=
+ +
1
Bµi 3.
Chøng minh r»ng:
1 sin cos
cos 1 sin
a a
a a

−
=
+
Bµi 4.
Cho
4 4
sin cos 1a a
m n m n
+ =
+
. Chøng minh r»ng:
10 10
sin cos 1
4 4 4
( )
a a
m n m n
+ =
+
Bµi 5.
Cho
2 2 2 2 2 2 2 2 2
2 . . . . . 1tg a tg b tg c tg a tg b tg b tg c tg a tg c+ + + =
CMR:
2 2 2
sin sin sin 1a b c+ + =
Bµi 6.
Cho:
3 2
.cos .cos .sin

3 2
.sin .cos .sin
a x b x x m
a x b x x n

+ =


+ =


CMR:
3
2 2 2
3 3
( ) ( ) 2m n m n a+ + − =
Bµi 7.
cos 1
1/ .
1 sin cos
a
tga
a a
+ =
+

sin 1 cos 2
2 /.
1 cos sin sin
a a

a a a
+
+ =
+
2
cot 1
3/ . . 1
2
cot
1
tga g a
ga
tg a
−
=
−

1 cos 1 cos 4cot
4 /.
1 cos 1 cos sin
a a ga
a a a
+ −
− =
− +
2 2
5 / .(sin cos ) (sin cos ) 4sin .cosa a a a a a+ + − =
6 /.1 2sin .cos sin .cos .(1 ).(1 cot )a a a a tga ga+ = + +
2 2 2 2
7 / . sin .sintg a a tg a a− =

2
(sin cos ) 1
2
8/ . 2
cot sin .cos
a a
tg a
ga a a
+ −
=
−
Bµi 8.
2 2
sin cos
1 sin cos
1 cot 1
− − =
+ +
x x
x x
gx tgx
Bµi 9.
2 2
sin cos
1 sin cos
1 cot 1
− − =
+ +
x x

x x
gx tgx
Bµi 10.
A, sin
4
x-cos
4
x=1-2cos
2
x B, sin
4
x+cos
4
x=1-2cos
2
x.sin
2
x
C, sin
6
x+cos
6
x=1-3sin
2
x.cos
2
x D, sin
8
+cos
8

x=1-4sin
2
x.cos
2
x+2sin
4
x.cos
4
x
Bµi 11.
sin
2
x-tg
2
x=tg
6
x(cos
2
x-cotg
2
x)
3 3
3 3
2 2
1 cot
cot
sin sin .cos cos
− + = +
tg x g x
tg x g x

x x x x
Bµi 12.
A,
sin
1
3
cos (1 cos )
sin
−
=
+
tgx x
x x
x
B,
sin cos 1 cos
sin cos 1 1 sin
x x x
x x x
+ −
=
− + +
2
Bµi 13.
Cho
sin
1
sin .sin
2
cos .cos

3







=
=
=
a x
a x y
a x y
CMR:
2 2 2
1 2 3
1a a a
+ + =
sin
1
sin .sin
2
cos .cos .sin
3
cos .cos .cos
4










=
=
=
=
a x
a x y
a x y z
a x y z
CMR:
2 2 2 2
1 2 3 4
1a a a a
+ + + =
II- Rót gän biÓu thøc
Bµi 14.
A=cos
2
x+cos
2
x.tg
2
x
1 1
1 1

cos cos
B tgx tgx
x x
  
= + + + −
 ÷ ÷
  

2
2cos 1
sin cos
x
C
x x
−
=
+
cos sin
2 2
sin 1 cos 1
sin cos
x x
D x x
x x
 
 
 ÷
 ÷
 
 

= + + + E=(tgx+cotgx)
2
-(tgx-cotgx)
2
Bµi 15.
2 2
sin
2 2
cos cot
x tg x
A
x g x
−
=
−

2 2 2
2 2 2
cos cos .cot
sin sin .
x x g x
B
x x tg x
+
=
+
cos
sin cot
tga a
C

a ga
= −

2 2 4
2 2 4
sin cos cos
cos sin sin
x x x
N
x x x
− +
=
− +
Bµi 16.
cos .cot sin .
1 1
sin cos
a ga a tga
A
a a
−
=
−

1 sin 1 sin
1 sin 1 sin
x x
B
x x
+ −

= +
− +
( )
2
1 sin cot 1 cotC x gx gx= − + −
III- Chøng minh c¸c biÓu thøc sau kh«ng phô thuéc x
Bµi 17.
A=cos
4
x-sin
4
x+2sin
2
x (=1) B=cos
4
x+sin
2
x.cos
2
x+sin
2
x (=1)
C=2(cos
6
x+sin
6
x)-3(sin
4
x+cos
4

x) (=-1) D=3(sin
8
x-cos
8
x)+4(cos
6
x-2sin
6
x)+6sin
4
x (=1)
E=
4 2 4 2
sin 4cos cos 4sinx x x x+ + +
(=3)
Bµi 18.
Cho
.sin .sin .cos .cos 0a b
α β α β
− =
3
CMR:
2 2 2 2
1 1
.sin .cos .sin .cos
S
a b a b

= +
+ +

Không phụ thuộc vào
;

.
Bài 19.
Cho x,y thoả mãn:
2 2 2 2
2 2 2 2
1
cos sin 1
.sin .cos
m tg x n tg y
m x n y
m x n y

+ =

+ =


=

. Tìm hệ thức giữa m, n không chứa x,y.
Đ/s:
4 4
2 2
2 2 2 2
2 2
1
1 1

m n
m n
m n m n
+ = + +
+ +
Bài 20.
A=2(sin
4
x+cos
4
x+sin
2
x.cos
2
x)
2
-(sin
8
x+sin
8
x) B=sin
6
x+cos
6
x-2sin
4
x-cos
4
x+sin
2

x
4 4
6 6
sin cos 1
sin cos 1
x x
C
x x
+
=
+
D=(sin
4
x+cos
4
x-1)(tg
2
x+cotg
2
x+2)
2 2
2
cot cos sin .cos
cot
sin
g x x x x
E
gx
x

= +

2 2 2 2
2 2
cos cot cos
sin cos
tg x x g x x
F
x x

= +
2
6
6 2
1 3.
cot cos
tg x
G tg x
g x x
= H=cos
2
x.cotg
2
x+5cos
2
x-cotg
2
x+4sin
2
x

I=(1+cotgx)sin
3
x+(1+tgx)cos
3
x-sinx-cosx
( ) ( )
2
2
2 2
1
1 1 cos
tg x
K tg x x
tgx


= + +
ữ

M=sin
8
x+cos
8
x+6sin
4
x.cos
4
x+4sin
2
x.cos

2
x(sin
4
x+cos
4
x)
Bài 21.
Cho S=sin
6
x+cos
6
x-m(sin
4
x+cos
4
x)
1/. Tìm m đề S không phụ thuộc x. 2/. Tìm giá trị của S với m tìm đợc.
Bài 22.
Cho S=m(cos
8
x- sin
8
x)+4(cos
6
x-sin
6
x)+nsin
4
x
1/. Tìm m,n đề S không phụ thuộc x. 2/. Tìm giá trị của S với m,n tìm đợc.

Bài 23.
Cho S=sin
6
x+cos
6
x+a(sin
4
x+cos
4
x)+4(a+1)sin
2
x.cos
2
x
Tìm a đề S không phụ thuộc x.
IV- Tính giá trị của các biểu thức l ợng giác
Bài 24.
Cho sinx+cosx=4/5
Tính giá trị các biểu thức sau:
A=sinx.cosx (9/50) B=sinx-cosx C=sin
3
x-cos
3
x
Bài 25.
Cho tgx-cotgx=3
Tính các giá trị của biểu thức sau: A=tg
2
x+cotg
2

x B=tgx+cotgx C=tg
4
x-cotg
4
x
4
Bài 26.
Cho tgx=2
Tính các giá trị của biểu thức sau:
.....
Bài 27.
Cho sinx+cosx=m.
Tính các giá trị của biểu thức sau: A=sinx.cosx B=sinx-cosx C=sin
3
x+cos
3
x
D=sin
4
x-cos
4
x E=sin
5
x+cos
5
x F= sin
6
x+cos
6
x G= sin

8
x+cos
8
x H= sin
7
x-cos
7
x
Bài 28.
Cho sinx-cosx=m
Tính các giá trị của biểu thức sau: A=sinx+cosx B=sin
3
x-cos
3
x C= sin
4
x+cos
4
x
D= sin
5
x-cos
5
x E= sin
6
x-cos
6
x F= sin
7
x-cos

7
x G= sin
8
x+cos
8
H= sin
9
x-cos
9
x
Bài 29.
Cho tgx+cos tgx=m
Tính các giá trị của biểu thức sau: A=tg
2
x+cotg
2
x B= tg
3
x-cotg
3
x C= tg
4
x+cotg
4
x
D= tg
5
x-cotg
5
x E= tg

6
x+cotg
6
x
Bài 30.
Cho tgx-cotgx=m
Tính các giá trị của biểu thức sau: A=tg
2
x-cotg
2
x B= tg
3
x-cotg
3
x C= tg
4
x-cotg
4
x
D= tg
5
x-cotg
5
x E= tg
8
x+cotg
8
x
Bài 31.
Tìm Max, min của:

2 2
2 2
3sin 4sin .cos 9 cos
( )
7sin 2sin .cos 4cos
x x x x
f x
x x x x
+ +
=
+
Bài 32.
Cho 3sin
4
x-cos
4
x=1/2. Tính: A=sin
4
x+3cos
4
x
Bài 33.
Cho 3sin
4
x+2cos
4
x=98/81. Tính: A=2sin
4
x-5cos
6

x
Bài 34.
Cho sin
4
x+2cos
4
x=1. Tính: A=5sin
6
x-8cos
8
x
Bài 35.
Cho 17cos
4
x-5sin
4
x=7. Tính: A=9sin
8
x-2cos
6
x
Phần 2: góc liên quan đặc biệt
Bài 36.
Tính giá trị của các biểu thức:
0 0
0 0
cos750 sin 420
sin( 330 ) cos( 390 )
A
+

=


0 0
0
1 cos1860 ( 390 )
( 420 )
tg
B
tg
+
=

0 0
0 0
495 ( 696 )
cot 1935 cot 765
tg tg
C
g g
+
=

sin( 4,8 ).sin( 5,7 ) cos( 6,7 ).cos( 5,8 )
cos( 5,2 ) ( 6,2 )
D
tg

= +

5