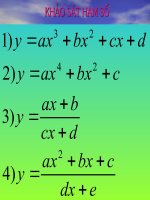CHỦ đề 1 vấn đề 5 KHẢO sát sự BIẾN THIÊN – đồ THỊ của hàm số image marked

VẤN ĐỀ 5: KHẢO SÁT SỰ BIẾN THIÊN – ĐỒ THI ̣CỦ A HÀ M SỐ
LÝ THUYẾT CĂN BẢN CẦN NẮM VỮNG
Sơ đồ khảo sát hàm số :
1) Tìm tập xác định.
2) Sự biến thiên
a) Xét chiều biến thiên của hàm số.
i) Tính đạo hàm y’
ii) Tìm các điể m ta ̣i đó đa ̣o hàm y’ bằ ng 0 hoă ̣c không xác đinh
̣
iii) Xét dấ u đa ̣o hàm y’ và suy ra chiề u biế n thiên của hàm số
b) Tìm cực tri ̣
c) Tìm các giới ha ̣n ta ̣i vô cực, các giới ha ̣n vô cực và tim
̀ tiê ̣m câ ̣n (nế u có)
d) Lâ ̣p bảng biế n thiên.
3) Dựa vào bảng biế n thiên và các yế u tố xác đinh
̣ ở trên để vẽ đồ thi.̣
MINH HỌA
Mời ba ̣n đo ̣c qua các ví du ̣ trong SGK Giải tích 12 (trang 32 – 41). Ở đó đã trình bày các ví
dụ rất chi tiết, nôn tác già không giải thích gì thêm ở phần này.
Chú ý:
1) Nếu hàm số tuần hoàn với chu kì T thì chỉ cần khảo sát sự biến thiên và vẽ đồ thị trên một
chu kì, sau đó tịnh tiến dồ thị song song với trục Ox.
2) Nên tính thêm tọa độ một số điể m, đặc biệt là tọa độ các giao điểm của đồ thị với các trục
tọa độ. Nên lưu ý đế n tính chẵn, lè của hàm số và tính đối xứng của đồ thị để vẽ cho chính
xác.
Sư ̣ tương giao của các đồ thi:̣
- Giả sử hàm số y = f ( x ) có đồ thi ̣ ( C1 ) và hàm số y = g ( x ) có đồ thi ̣ ( C2 ) . Để tìm hoành
đô ̣ giao điể m của ( C1 ) và ( C2 ) , ta phải giải phương trình f ( x ) = g ( x ) . Giả sử phương trình
trên có nghiê ̣m là

x 0 , x1 ,... Khi đó, các giao điể m của

( C1 )

và

( C2 )

là

M0 ( x 0 ,f ( x 0 ) ) , M1 ( x1;f ( x1 ) )
MINH HỌA
1) Tim
̀ giao điể m của ( C1 ) và ( C2 ) , lầ n lươ ̣t là đồ thi ̣ của hàm số y = f ( x ) =

1+ x
và
2−x

y = g ( x ) = x2

Trang 1 – Website chuyên đề thi thử file word có lời giải


Phương triǹ h hoành đô ̣ giao điể m

2−x  0

−6 − x
= x2  
2  x =3

2−x
−6 − x = ( 2 − x ) .x

Vâ ̣y giao điể m của ( C1 ) và ( C2 ) là ( 3;9)
2) Tim
̀ m để đồ thi ̣của hàm số y = f ( x ) =

1+ x
và đường thẳ ng y = g ( x ) = mx cắ t nhau ta ̣i
2−x

hai điể m phân biê ̣t.
- Phương triǹ h hoành đô ̣ giao điể m:

−6 − x
= mx (1)
2−x

2−x  0
2−x  0




2
−6 − x = ( 2 − x ) .mx
−mx + ( 2m + 1) x + 6 = 0 ( 2 )
- Đồ thi ̣ của hàm số y = f ( x ) =

1+ x

và đường thẳ ng y = g ( x ) = mx cắ t nhau ta ̣i hai điể m
2−x

phân biê ̣t.

 Phương triǹ h (1) có hai nghiê ̣m phân biê ̣t.
 Phương triǹ h (2) có hai nghiê ̣m phân biê ̣t khác 2.

−7 + 4 3
m 
 = ( 2m + 1) − 4 ( − m ) .6  0
 = 4m + 28m + 1  0
2



2

80
−7 − 4 3
 −m.2 + ( 2m + 1) .2 + 6  0

m 

2
2

2

Da ̣ng đồ thi ̣của hàm số bâ ̣c ba: y = ax3 + bx 2 + cx + d ( a  0 )

a 0
Phương
y' = 0

nghiê ̣m

a0

triǹ h
có hai
phân

biê ̣t.

Trang 2 – Website chuyên đề thi thử file word có lời giải


Phương

triǹ h

y' = 0

có

nghiê ̣m kép.

Phương

trình

y' = 0

vô

nghiê ̣m

Da ̣ng đồ thi ̣của hàm số : y = ax 4 + bx 2 + c ( a  0)

a 0
Phương
y' = 0

nghiê ̣m

a0

triǹ h
có

ba
phân

biê ̣t

Phương

triǹ h

y ' = 0 có mô ̣t

nghiê ̣m

Trang 3 – Website chuyên đề thi thử file word có lời giải


Da ̣ng của đồ thi cu
̣ ̉ a hàm số : y =

a 0

ax + b
( c  0, ad − bc  0 )
cx + d

a0

Trang 4 – Website chuyên đề thi thử file word có lời giải