D06 diện tích hình phẳng y=f(x), y=g(x), y=h(x) muc do 2
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (138.47 KB, 6 trang )
Câu 50:
[2D3-5.6-2] (THPT TRẦN PHÚ ĐÀ NẴNG – 2018)Cho hình
hình phẳng giới hạn bởi parabol
, đường cong
hoành (phần tô đậm trong hình vẽ). Tính diện tích
A.
.
B.
.
C.
và trục
của hình
.
là
.
D.
.
Lời giải
Chọn B
Parabol
Phương
có đỉnh
trình
hoành
độ
.
giao
điểm
của
và
là
.
Ta có
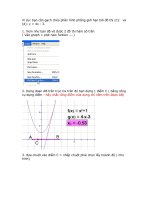
.Câu 37: [2D3-5.6-2] (Toán Học Tuổi Trẻ - Số 5 - 2018 BTN) Tính diện tích hình phẳng giới hạn bởi đồ thị
tại
A.
và
và các tiếp tuyến của
.
.
B.
.
C.
.
D.
Lời giải
Chọn A
Ta có
Tiếp tuyến của
.
tại
và
Giao điểm của hai tiếp tuyến là
lần lượt là
;
.
.
.
Khi
đó,
dựa
và
hình
vẽ
ta
có
diện
tích
hình
phẳng
cần
tìm
là:
.
Câu 9:
[2D3-5.6-2](Đề thi lần 6- Đoàn Trí Dũng - 2017 - 2018)Tính diện tích
của hình phẳng giới
hạn bởi các đường
A.
.
B.
.
C.
D.
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm
.
.
Câu 14: [2D3-5.6-2](CHUYEN PHAN BOI CHAU_NGHE AN_L4_2018_BTN_6ID_HDG) Tính
diện tích hình phẳng giới hạn bởi các đường
A.
.
B.
.
,
C.
Lời giải
Chọn C
,
.
.
D.
.
Xét phương trình hoành độ giao điểm:
;
;
Ta có :
.
.
.
Câu 37. [2D3-5.6-2] (SGD Bình Dương - HK 2 - 2017 - 2018 - BTN) Diện tích
hạn bởi đồ thị hàm số
A.
.
, trục hoành và đường thẳng
B.
.
C.
của hình phẳng giới
là
.
D.
.
Lời giải
Chọn B
Xét phương trình
.
.
Câu 5160: [2D3-5.6-2][Cụm6HCM - 2017] Gọi
số
là hình phẳng giới hạn bởi đồ thị
và trục hoành. Hai đường thẳng
diện tích bằng nhau. Tính
chia hình
.
của hàm
thành ba phần có
A.
.
B.
.
C.
.
D.
.
Lời giải
Chọn B
Cách1: (Dùng công thức diện tích theo biến
+ Gọi
).
. Suy ra:
.
Ta có:
.
+ Gọi
.
Suy ra:
Mà
.
nên
.
+ Gọi
.
Suy ra:
Mà
Vậy
.
nên
.
.
Cách2: (Dùng công thức diện tích theo biến
Từ điều kiện bài toán ta có :
).
.
Xét các phương trình hoành độ giao điểm :
.
và
Gọi
.
;
;
.
Khi đó ta có :
.
=
=
.
.
Chứng minh tương tự ta có :
Theo bài ra ta có :
Do đó
và
và
Vậy
.
.
.
.
Câu 5172:[2D3-5.6-2][BTN169 - 2017] Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới
hạn bởi
,
quanh trục hoành là:
A.
(đvtt).
B.
(đvtt).
C.
(đvtt).
D.
(đvtt).
Lời giải
Chọn D
Thể tích khối tròn xoay là:
.
Câu 5185: [2D3-5.6-2][THPTChuyênHàTĩnh - 2017] Diện tích hình phẳng giới hạn bởi nhánh đường
cong
với
, đường thẳng
và trục hoành bằng:
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Phương trình hoành độ giao điểm
và
là
.
Hoành độ giao điểm
Hoành độ giao điểm
Khi đó ta có:
và
là
và
.
là
.
.