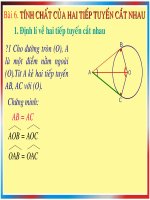Tính chất hai tiếp tuyền cắt nhau1

.
O
O
A
A
C
C
B
B
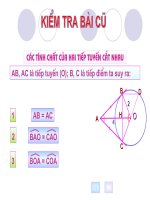
C¸c tÝnh chÊt cña hai tiÕp tuyÕn c¾t nhau
AB, AC lµ tiÕp tuyÕn (O); B, C lµ tiÕp ®iÓm ta suy ra:

AB = AC1
BAO = CAO
2
BOA = COA3
D
D
H
H
H
2
2
4
4

Tiết 29:
Tiết 29:

Luyện tập

Bài 30 SGK tr.116:
Bài 30 SGK tr.116:
Cho nửa đường tròn tâm O có đường kính
Cho nửa đường tròn tâm O có đường kính
AB
AB
(đường kính của một đường tròn chia đường tròn đó thành
(đường kính của một đường tròn chia đường tròn đó thành
hai nửa đường tròn).
hai nửa đường tròn).
Gọi Ax, By là các tia vuông góc với AB
Gọi Ax, By là các tia vuông góc với AB
(Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ
(Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ
AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ
AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ
tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C
tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C
và D. Chứng minh rằng:
và D. Chứng minh rằng:


a) COD = 90
a) COD = 90
0
0
.
.

b) CD = AC + BD.
b) CD = AC + BD.


c) Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.
c) Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.

Gi¶i
Gi¶i


Tõ (1) suy ra AC.BD = CM.MD. Trong tam gi¸c COD
Tõ (1) suy ra AC.BD = CM.MD. Trong tam gi¸c COD
vu«ng t¹i O, OM lµ ®/c (OM
vu«ng t¹i O, OM lµ ®/c (OM
⊥
⊥
CD t/c tiÕp tuyÕn) ta cã: –
CD t/c tiÕp tuyÕn) ta cã: –
CM.MD = OM
CM.MD = OM
2
2
(HTL trong tam gi¸c vu«ng). Tõ ®ã suy ra
(HTL trong tam gi¸c vu«ng). Tõ ®ã suy ra
CM.MD = OM
CM.MD = OM
2
2

= R
= R
2
2
(
(
R lµ BK cña (O)
R lµ BK cña (O)
) (
) (
kh«ng ®æi
kh«ng ®æi
)
)
A
A
B
B
C
C
•
•
O
O
D
D
y
y
x
M

M


Ta cã: CM = CA, DM = DB (
Ta cã: CM = CA, DM = DB (
t/c 2 tiÕp tuyÕn c¾t nhau
t/c 2 tiÕp tuyÕn c¾t nhau
) (1)
) (1)


⇒
⇒


CM + DM = CA + DB hay CD = AC + BD.
CM + DM = CA + DB hay CD = AC + BD.


V× Ax
V× Ax
⊥
⊥
AB vµ By
AB vµ By
⊥
⊥
AB (gt)
AB (gt)
⇒

⇒
Ax vµ By
Ax vµ By
lµ tiÕp tuyÕn cña (O)
lµ tiÕp tuyÕn cña (O)

Ta cã: OC lµ ph©n gi¸c cña AOM, OD
Ta cã: OC lµ ph©n gi¸c cña AOM, OD


lµ ph©n gi¸c cña MOB (
lµ ph©n gi¸c cña MOB (
t/c hai tiÕp tuyÕn
t/c hai tiÕp tuyÕn
c¾t nhau
c¾t nhau
). Mµ AOM vµ MOB lµ 2 gãc kÒ
). Mµ AOM vµ MOB lµ 2 gãc kÒ
bï nªn OC
bï nªn OC
⊥
⊥
OD hay COD = 90
OD hay COD = 90
0
0
M
O
a) C/m COD = 90
a) C/m COD = 90

0
0
b) C/m CD = AC + BD
b) C/m CD = AC + BD
c) C/m AC.BD kh«ng ®æi khi M di chuyÓn trªn nöa ®.trßn
c) C/m AC.BD kh«ng ®æi khi M di chuyÓn trªn nöa ®.trßn


a) C/m 2AD = AB + AC BC
a) C/m 2AD = AB + AC BC


Ta có AD = AF, BD = BE, CF = CE
Ta có AD = AF, BD = BE, CF = CE
(
(
t/c 2 tiếp tuyến cắt nhau
t/c 2 tiếp tuyến cắt nhau
)
)






AB + AC BC = AD + DB + AF
AB + AC BC = AD + DB + AF
+ FC BE EC = AD + DB + AD +
+ FC BE EC = AD + DB + AD +

FC BD CF = 2AD
FC BD CF = 2AD


b) Các hệ thức tương tự ở câu a là:
b) Các hệ thức tương tự ở câu a là:


2BE = BA + BC AC
2BE = BA + BC AC


2CF = CA + CB AB
2CF = CA + CB AB


Bài 31 SGK tr.116:
Bài 31 SGK tr.116:
Trên hình 82, tam giác ABC
Trên hình 82, tam giác ABC
ngoại tiếp đường tròn (O).
ngoại tiếp đường tròn (O).


a) C/m rằng: 2AD = AB + AC BC.
a) C/m rằng: 2AD = AB + AC BC.


b) Tìm các hệ thức tương tự như hệ thức ở câu a.
b) Tìm các hệ thức tương tự như hệ thức ở câu a.

A
A
B
B
C
C
D
D
F
F
E
E
O
O
Hình 82
Giải
Giải
32 28


Bài 32 SGK tr.116:
Bài 32 SGK tr.116: Cho
tam giác đều ABC ngoại tiếp đường
tam giác đều ABC ngoại tiếp đường
tròn bán kính bằng 1cm. Diện tích của tam giác ABC bằng:
tròn bán kính bằng 1cm. Diện tích của tam giác ABC bằng:


(A) 6cm
(A) 6cm

2
2
(B) (C) cm
(B) (C) cm
2
2
(D) cm
(D) cm
2
2
Hãy chọn câu trả lời đúng.
Hãy chọn câu trả lời đúng.
2
2
3
3

cm
cm
4
4
3
3
3
3
3
3
3
3
1

1
D
D
O
O
A
A
B
B
C
C




HDVN