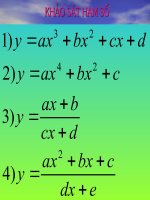Sơ đồ các bước khảo sát sự biến thiên và vẽ đồ thị hs

SƠ ĐỒ CÁC BƯỚC KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
1. Hàm bậc ba : y = ax
3
+ bx
2
+ cx + d (a ≠ 0)
a. TXĐ : D = R
b. Sự biến thiên :
+. Chiều biến thiên: Đạo hàm y’ = A x
2
+ Bx + C ( Tính
∆
) , Sau đây là các khả năng
có thể xẩy ra :
TH1:



<
<∆
0A
0

⇒ y’ < 0 với mọi x
∈
R ⇒ HS nghòch biến trên R (1)
TH2:




>
<∆
0A
0

⇒ y’ > 0 với mọi x
∈
R ⇒ HS đồng biến trên R (2)
TH3:



<
=∆
0A
0

⇒ y’ ≤ 0 với mọi x
∈
R ⇒ HS nghòch biến trên R (3)
TH4:



>
=∆
0A
0
⇒ y’ ≥ 0 với mọi x
∈

R ⇒ HS đồng biến trên R (4)
TH5, 6:
∆
> 0 . Cho y’= 0 ⇔



=⇒=
=⇒=
)x(fyxx
)x(fyxx
22
11
(5) và (6)
Căn cứ vào BBT để kết luận các khoảng mà hàm số tăng hoặc giảm
+. Cực trò :
* Các TH1, TH2, TH3, TH4 : Kết luận không có cực trò
* TH5: Hàm số đạt cực đại tại x = x
1
và y
CĐ
= f(x
1
)
Hàm số đạt cực tiểu tại x = x
2
và y
CT
= f(x
2

)
* TH6: Hàm số đạt cực tiểu tại x = x
1
và y
CT
= f(x
1
)
Hàm số đạt cực đại tại x = x
2
và y
CĐ
= f(x
2
)
+. Giới hạn: a > 0 :
=
∞−→
Limy
x
-∞ ,
=
∞+→
Limy
x
+ ∞ ; a < 0 :
=
∞−→
Limy
x

+∞ ,
=
∞+→
Limy
x
- ∞
+. Bảng biến thiên : (Ứng với các trường hợp đạo hàm phía trên )
c. Đồ thò :
+. Điểm đặc biệt : Tìm gđ của đồ thò (C) với Ox và Oy; điểm CT ; lấy thêm vài điểm khác
+. Vẽ đồ thò : Gồm các bước : Vẽ hệ tục ; Lấy điểm đặc biệt ; Vẽ đồ thò . (Các dạng
đồ thò )
)x(f
1
∞+
∞−
CT
CĐ
)x(f
2
∞−
∞+
CĐ
CT
)x(f
1
)x(f
2
_
∞+
∞−

+
∞+
∞−
x
'y
y
)1(
∞+
∞−
−
∞+
∞−
x
'y
y
)2(
A2
B
−
∞+
∞−
+
∞+
∞−
x
'y
y
)3(
+
0

A2
B
−
_
∞+
∞−
∞+
∞−
x
'y
y
)4(
0
−−
∞+
∞−
+
x
'y
y
)5(
+
0
0
−
1
x
2
x
∞+

∞−
+
x
'y
y
)6(
+
0
0
−
1
x
2
x
)1(
)2(
)3(
)4( )5( )6(
2. Hàm trùng phương : y = ax
4
+ bx
2
+ c (a ≠ 0 )
a. TXĐ : D = R
b. Sự biến thiên:
+. Chiều biến thiên: Đạo hàm y’ = 4ax
3
+ 2bx = x (4ax
2
+ 2b). Có thể xẩy ra 1 trong

4 trường hợp sau:
TH1: Nếu a < 0 và b < 0 thì y’= 0 ⇔ x = 0 ⇒ y = f(0) . Xem BBT để kết luận
khoảng tăng , giảm (1)
TH2: Nếu a > 0 và b > 0 thì y’= 0 ⇔ x = 0 ⇒ y = f(0) . Xem BBT để kết luận
khoảng tăng , giảm (2)
TH3: Nếu a < 0 và b > 0 thì y’= 0 ⇔





=⇒=
=⇒=
=⇒=
)x(fyxx
)0(fy0x
)x(fyxx
22
11
. Xem BBT để kết luận
khoảng tăng , giảm (3)
TH4: Nếu a > 0 và b < 0 thì y’= 0 ⇔





=⇒=
=⇒=
=⇒=

)x(fyxx
)0(fy0x
)x(fyxx
22
11
. Xem BBT để kết luận
khoảng tăng , giảm (4)
+. Cực trò :
TH 1: Hàm số đạt cực đại tại x = 0 và y
CĐ
= f(0)
TH 2: Hàm số đạt cực tiểu tại x = 0 và y
CT
= f(0)
TH 3: Xem BBT để kết luận
TH 4: Xem BBT để kết luận
+. Giới hạn: a> 0 :
=
∞−→
Limy
x
+∞ và
=
∞+→
Limy
x
+ ∞ ; a< 0 :
=
∞−→
Limy

x
-∞
và
=
∞+→
Limy
x
- ∞
+. Bảng biến thiên :
c. Đồ thò :
* Điểm đặc biệt : Tương tự như HS bậc ba
* Vẽ đồ thò : Thứ tự các bước vẽ như HS bậc ba. Các dạng đồ thò của hàm trùng phương
ứng với các trường hợp như sau :

y’
x
y
∞+
+
0
∞−
0
_
∞−
∞−
CĐ
f(0
)
(1)
y’

x
y
∞+
+
0
∞−
0
_
∞+
∞+
CT
f(0)
(2)
y’
x
y
∞+
+
∞−
0
_
∞−
∞−
(3)
x
1
0
0 0
x
2

+
_
CT
f(0)
0
y’
x
y
∞+
+
0
_
∞+
∞+
CĐ
f(0)
(4)
x
1
0
0 0
x
2
+
_
0
∞−
)x(f
CD
1

)x(f
CD
2
)x(f
CT
1
)x(f
CT
2
)1(
)2(
)3(
)4(
c
a
∞−
∞+
_
∞+
∞−
+
x
'y
y
)1(
+
∞−
∞+
_
∞+

∞−
x
'y
y
)2(
−
−
c
a
c
a
c
a
c
d
−
c
d
−
3. Hàm nhất biến : y =
dcx
bax
+
+
( c ≠ 0 ; ad –bc ≠ 0 )
a. TXĐ : D = R \







−
c
d

b. Sự biến thiên:
+. Chiều biến thiên: Đạo hàm : y’ =
2
)dcx(
bcad
+
−
. Có thể xẩy ra 1 trong 2 trường hợp sau :
TH1: ad - bc > 0 ⇒ y’> 0 với mọi x∈D⇒ HS tăng trên 2 khoảng: (-∞,
c
d
−
);(
c
d
−
,+∞ )
(1)
TH2: ad - bc < 0 ⇒ y’< 0 với mọi x∈D⇒ HS giảm trên 2 khoảng: (-∞,
c
d
−
);(
c

d
−
,+∞ ) (2)
+. Cực trò: Không có
+. Tiệm cận : ( có TCĐ và TCN )
* y’ > 0 :
+∞=
−






−→
ylim
c
d
x
và
−∞=
+






−→
ylim

c
d
x
⇒ đường thẳng x =
c
d
−
là TCĐ
y’ < 0 :
−∞=
−






−→
ylim
c
d
x
va
+∞=
+







−→
ylim
c
d
x
⇒ đường thẳng x =
c
d
−
là TCĐ
*
c
a
ylim
x
=
±∞→
⇒ đường thẳng y =
c
a
là TCN
+. Bảng biến thiên :


c. Đồ thò :
* Điểm đặc biệt : Tìm giao điểm của đồ thò với các trục toạ độ ; Lấy thêm vài điểm khác
* Vẽ đồ thò : Gồm các bước : Vẽ hệ trục ; vẽ hai đường tiệm cận ; lấy điểm đặc biệt ,
từ đó vẽ đồ thò. Các dạng đồ thò ứng với 2 trường hợp trên như sau:
Đôi điều tâm sự:

Tại sao học sinh đi thi TN lại không được điểm 2, đi thi ĐH lại bò điểm không
0, thật đơn giản là không nắm vững bài toán khảo sát hàm số . Đây là bài toán
luôn có trong các kì thi nhưng nhiều học sinh vẫn không nắm được. Qua kinh
nghiệm giảng dạy mình đã lập sơ đồ này cho học sinh photo, đặc biệt là học
sinh yếu thì đều làm ro ro hết. Bây giờ mình xin chia xẻ cùng đồng nghiệp nhé.

Nếu thấy hiệu nghiệm, xin một lời cảm ơn vào đòa chỉ :

(1)
(2)
TCĐ
TCN
TCĐ
TCN