Tính chất của hai tiếp tuyến cắt nhau

Tr­êng THCS Gi¶ng Vâ
Gi¸o viªn d¹y: Vò Minh
NguyÖt

Víi “ th­íc ph©n gi¸c
“ ta cã thÓ t×m ®­îc t©m
cña mét vËt h×nh trßn

O
C
B
A
2
1
2
1
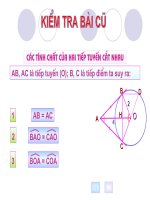
Chứng minh:
+/ AB, AC là hai tiếp tuyến tại B và C của (O)
=> AB

OB ; AC

OC ( T/c tiếp tuyến)
AB = AC
Â1 = Â2
Ô1 = Ô2
Hãy kể tên :

- Các đoạn thẳng bằng nhau
- Các góc bằng nhau


AB, AC thứ tự là các tiếp tuyến tại B và C của
AB, AC thứ tự là các tiếp tuyến tại B và C của
(O) (hình bên)
(O) (hình bên)
Bài toán: ?1
Bài toán: ?1
+/

AOB =

AOC (ch - cgv)


E
F
D
I
C
B
A

D, E, F n»m trªn (I)
KL
KL

∆

ABC. AI, BI, CI lµ ph©n gi¸c
c¸c gãc cña
∆
ABC.
ID
⊥
BC ; IE
⊥
AC; IF
⊥
ABGT
Đường tròn néi
tiếp tam giác
Tam giác
ngo iạ tiếp
đường tròn
Bµi to¸n: ?3
Bµi to¸n: ?3

2. ®­êng trßn néi tiÕp tam gi¸c
Kh¸i niÖm: (SGK/ tr114 -115)
+/ §­êng trßn tiÕp xóc víi ba
c¹nh cña mét tam gi¸c gäi lµ ®­
êng trßn néi tiÕp tam gi¸c, cßn
tam gi¸c gäi lµ ngo¹i tiÕp ®­êng
trßn.
+/ T©m cña ®­êng trßn néi tiÕp
tam gi¸c lµ giao ®iÓm cña c¸c
®­êng ph©n gi¸c c¸c gãc trong
cña tam gi¸c

E
F
D
I
C
B
Đường tròn néi
tiếp tam giác
Tam giác ngọai
tiếp đường tròn
A
b

E
F
D
I
C
B
A
x
y
z

I
A
B
M
P
N

K
C
Đường tròn bàng
tiếp tam giác

Kh¸i niÖm: (SGK/ tr 115)
+/ §­êng trßn tiÕp xóc víi mét
c¹nh cña mét tam gi¸c vµ phÇn
kÐo dµi cña hai c¹nh kia gäi lµ
®­êng trßn bµng tiÕp tam gi¸c
+/ T©m cña ®­êng trßn bµng tiÕp
tam gi¸c lµ giao ®iÓm cña hai ®­
êng ph©n gi¸c gãc ngoµi vµ ®­
êng ph©n gi¸c trong cña tam
gi¸c
3. ®­êng trßn bµng tiÕp tam gi¸c
A
B
M
P
N
K
C
Đường tròn
bàng tiếp
tam giác

A
B C
O

1
O
3
O
2

B
O
C
A
R
2R
30
0
30
0