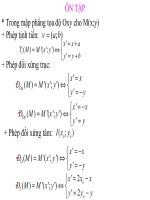on tap chuong 1 hinh hoc 11

ÔN TẬP
+ Phép tịnh tiến:

( ; )v a b=
r
'
( ) '( '; ')
'
v
x x a
T M M x y
y y b
= +

= ⇔

= +

r
+ Phép đối xứng trục:
* Trong mặp phẳng tọa độ Oxy cho M(x;y)
Ox
'
( ) '( '; ')
'
x x
D M M x y
y y
=


= ⇔

= −

Oy
'
( ) '( '; ')
'
x x
D M M x y
y y
= −

= ⇔

=

+ Phép đối xứng tâm:
( ; )
o o
I x y
O
'
( ) '( '; ')
'
x x
D M M x y
y y
= −


= ⇔

= −

' 2
( ) '( '; ')
' 2
o
I
o
x x x
D M M x y
y y y
= −

= ⇔

= −


+ Phép vị tự:
* Trong mặp phẳng tọa độ Oxy cho M(x;y) ,
( ; )
o o
I x y
( ; )
( ) '( '; ') '
' (1 )
' (1 )
I k

o
o
V M M x y IM k IM
x kx k x
y ky k y
= ⇔ =
= + −

⇔

= + −

uuuur uuur
Ví dụ: Trong mặt phẳng Oxy cho điểm I(1;2) ,
,A(2;3). Tìm Tọa độ ảnh A’ của A qua phép:
( 1;3)v = −
r
)
v
a T
r
Ox
)b D
( ,2)
)
I
d V
Oy
)c D

+ Phép tịnh tiến theo
( ; )v a b=
r
' 2 ( 1) ' 1
( ) '( '; ') '(1;6)
' 3 3 ' 6
v
x x
T A A x y A
y y
= + − =
 
= ⇔ ⇒
 
= + =
 
r
+ Phép đối xứng trục Ox:
Ox
' 2
( ) '( '; ') '(2; 3)
' 3
x
D A A x y A
y
=

= ⇔ ⇒ −

= −


Oy
' 2
( ) '( '; ') '( 2;3)
' 3
x
D A A x y A
y
= −

= ⇔ ⇒ −

=

+ Phép đối xứng tâm O:
O
' 2
( ) '( '; ') '( 2; 3)
' 3
x
D A A x y A
y
= −

= ⇔ ⇒ − −

= −

' 2.1 2 ' 0
( ) '( '; ') '(0;1)

' 2.2 3 ' 1
I
x x
D A A x y A
y y
= − =
 
= ⇔ ⇔ ⇒
 
= − =
 
Giải: Cho mpOxy, điểm I(1;2) ,A(2;3),
Tìm Tọa độ ảnh A’ của A qua phép:
( 1;3)v = −
r
+ Phép đối xứng trục Oy:
+ Phép đối xứng tâm I:

Viết phương trình ảnh của đường thẳng qua phép biến hình:
B1: Gọi đường thẳng d’ là ảnh của đường thẳng d qua phép biến
hình, M’(x’;y’) là ảnh của điểm qua phép biến hình.
( ; )M x y d∈
' 'M d
⇒ ∈
B2: Tìm tọa độ điểm M theo tọa độ điểm M’( dựa vào định
nghĩa, tính chất và biểu thức tọa độ của các phép biến hình)
B3: Thay tọa độ điểm M vừ tìm được vào phương trình đường
thẳng d sau đó khai triển rút gọn được mối liên hệ giữa các tọa
độ của điểm M’(có dạng phương trình tổng quát của đường
thẳng), đó chính là phương trình của đường thẳng d’.

B4: Kết luận phương trình đường thẳng d’.
Phương pháp:
Tiếp

ÔN TẬP
+ Phép tịnh tiến theo

( ; )v a b=
r
' '
( ) '( '; ')
' '
v
x x a x x a
T M M x y
y y b y y b
= + = −
 
= ⇔ ⇔
 
= + = −
 
r
+ Phép đối xứng trục:
* Trong mặp phẳng tọa độ Oxy cho M(x;y)
Ox
'
( ) '( '; ')
' '
x x x x

D M M x y
y y y y
= =
 
= ⇔ ⇔
 
= − = −
 
Oy
' '
( ) '( '; ')
' '
x x x x
D M M x y
y y y y
= − = −
 
= ⇔ ⇔
 
= =
 
+ Phép đối xứng tâm:
( ; )
o o
I x y
O
' '
( ) '( '; ')
' '
x x x x

D M M x y
y y y y
= − = −
 
= ⇔ ⇔
 
= − = −
 
' 2 2 '
( ) '( '; ')
' 2 2 '
o o
I
o o
x x x x x x
D M M x y
y y y y y y
= − = −
 
= ⇔ ⇔
 
= − = −
 
Về