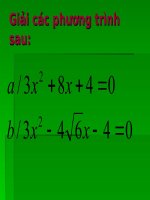tiến trình dạy bài Công thức nghiệm thu gọn toán 9

Giáo viên thực hiện: HỒNG NGỌC QUÝ
Trường THCS Quách Phẩm Bắc


1. Hãy điền vào chỗ ………..…để hồn chỉnh cơng thức nghiệm
của phương trình bậc hai: ax2 + bx + c = 0 (a ≠ 0)
nghiệm phân biệt
Nếu ∆ > 0 thì phương trình có 2…………………...……………..
……

b2 – 4ac

∆ = ….……………

 b 
x2 = ……………
2a

x1 = ……………
;
=0
Nếu ∆………. thì phương trình có nghiệm kép
-b
2a
x 1 = x2 = ……………
<0

Nếu ∆ ……….. thì phương trình vơ nghiệm.

2. Áp dụng cơng thức nghiệm giải các phương trình sau:
a) 5x2 + 4x – 1 = 0

;

b) x 2  2 3x  3 0


Giải
a) 5x2 + 4x – 1 = 0
(a = 5; b = 4 ; c = –1)
Ta có: Δ = 42 – 4.5.(– 1) = 16 + 20 =36
Do Δ = 36 > 0 nên phương trình có hai nghiệm phân biệt:
 4  36  4  6
 4  36  4  6 1

 1
x1 


; x2 
2.5
10
2.5
10
5
b) x 2  2 3x  3 0

(a = 1; b = 2 3 ; c = 3)
Ta có:  (2 3)2  4.1.3 = 12 – 12 =0
Do Δ = 0 nên phương trình có nghiệm kép:

2 3
x1  x 2 

2.1

3


- Cách 1: a phơng trình bậc hai về phơng trình tích.
- Cách 2: Giải bằng phơng pháp vẽ đồ thị Parbol và
đờng thẳng để tìm toạ độ điểm chung. Giá trị hoành độ
tìm đợc là nghiệm của phơng trình.
- Cách 3: Dùng hằng đẳng thức bình phơng của 1 tổng
(hoặc 1 hiệu). Biến đổi phơng trình về dạng
2
... ... số để lập luận
- Cách 4: Dùng công thøc nghiÖm.


? Trong các cách nêu đó,
cách nào áp dụng giải được
tất cả
mọi
trình
Trong cho
trường
hợp
hệ phương
số b là số
chẵn ta cịn

hainghiệm
mà emngắn
thấy gọn
dễ áp
có cơngbậc
thức
hơn, giải ra
nghiệm nhanhdụng
hơn. nhất.
Đó là: CƠNG THỨC NGHIỆM THU GỌN.


§5. c«ng thøc nghiƯm thu gän
1. Cơng thức nghiệm thu gọn.
Phương trình ax2 + bx + c = 0 (a ≠ 0).
Trong nhiều trường hợp ta đặt b = 2b’ (b’ = b : 2)
thì Δ = b2 – 4ac = (2b’)2 – 4ac = 4b’2 – 4ac = 4(b’2 – ac)
Kí hiệu : Δ’ = b’2 – ac. Ta có : Δ = 4Δ’
D.ựHãy
a vào
ẳngchth
ức Δ trong
= 4Δ’.
điềnđvào
ỗ ……
phiếu học tập theo mẫu sau:
?1 SGK

* Nếu ∆ > 0 thì ∆’ > 0 , phương trình có hai nghiệm phân biệt:
Hãy

nhận xét về dấu của Δ và ∆’ ?
'  '
 b    2b' 4 '  2b' 2  ' 2(  b'  ')  b (1)
…………..




x1 =
2a
2a
2a
2a
a
b'(5)
 '
 2b'
 2b'
2( (4)
b '  ') …………
(3) 2  ' …………
(2) 4 ' = …………
x2 =  b   …………
=
=
2a
2a
2a
2a
a

* Nếu ∆ = 0 thì …………
(6)= ,0phương trình
(7) ệm kép
có
nghi
Δ’
……………..
b
2b'
b'
(8)
(9)
……….
…………



x1 = x2 =
2a = 2a
a
* Nếu ∆ < 0 thì ………..
vơ (11)
nghiệm
Δ’ <(10)
0, phương trình
……………..


§5. CƠNG THỨC NGHIỆM THU GỌN
1. Cơng thức nghiệm thu gọn.

Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và b = 2b’, ’ = b’2 – ac :
Nếu ∆’ > 0 thì phương trình có hai nghiệm phân biệt:
 b'  '
 b '  '
x1 =
; x2 =
a
a
b'
 Nếu ∆’ = 0 thì phương trình có nghiệm kép: x1 = x2 = 
a
 Nếu ∆’ < 0 thì phương trình vơ nghiệm.
2. Áp dụng.
Ví dụ 1: Giải phương trình 5x2 + 4x – 1 = 0 bằng cách điền vào những
chỗ trống sau:
5
Giải Ta có: a =……..
; b’ = . .2…. ; c = . –. . .1
2
– ac =22 – 5.(– 1)= 4 + 5 = 9
Δ’ = b’
. …………………………………………………….…
Δ' .....................
9 =3
 b ' Δ '  2  3 1

 ;
Nghiệm của phương trình: x1 = …………………………………….
a
5

5
 b' Δ '  2  3

 1
x2 =……..…...………………………………
a
5


§5. CƠNG THỨC NGHIỆM THU GỌN
1. Cơng thức nghiệm thu gọn.
2. Áp dụng.
Ví dụ 2: Giải các phương trình sau:
2
a) 3x2 + 8x + 4 = 0 ; b)x 2  2 3x  3 0 ; c) 7x  4 3x  2 0
Giải
2
a) 3x2 + 8x + 4 = 0
b) x  2 3x  3 0
(a = 3; b’ = 4 ; c = 4)
(a = 1; b’ = 3 ; c = 3)
Ta có: Δ’ = 42 – 3.4 = 4 > 0
Ta có:  ' ( 3 )2  1.3 = 3 – 3 = 0
Do Δ’ > 0 nên phương trình có
2 nghiệm phân biệt:

x1

 b'  '
= a

x2 =

Do Δ’ = 0 nên phương trình có nghiệm kép:

=

 b'  '
a

–4+2

=

=

3
–4–2
3

–2
3
= –2

 b'  3

 3
a
1
2

7x
 4 3x  2 0
c)
x1 x 2 

(a = 7; b’ = 2
Ta có:

 '  2


3 


2

3

; c = 2)

 7.2 =

12 – 14 = –2

Do Δ’ = –2 < 0 nên phương trình vơ
nghiệm.


CỦNG CỐ VÀ LUYỆN TẬP
Xác

định kiến
kiến thức
thức cần
trọng
tâm
của bài
bàihọc:
học
A.
Những
nắm
trong

- Công thức nghiệm thu gọn.
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và b = 2b’, Δ’=b’2 – ac :
Nếu ∆’ > 0 thì phương trình có hai nghiệm phân
biệt :
 b '  '
 b '  '
x2 =
x1 =
;
a
a
 Nếu ∆’ = 0 thì phương trình có nghiệm kép :
b'
x1 = x2 =  a
 Nếu ∆’ < 0 thì phương trình vơ nghiệm.
-

Các bước giải phương trình bậc hai bằng cơng thức nghiệm thu gọn.
+ Xác định các hệ số a, b’ và c
+ Tính ∆’ và xác định ∆’ > 0 hoặc ∆’ = 0 hoặc ∆’ < 0
+ Tính nghiệm của phương trình (nếu có)


CỦNG CỐ VÀ LUYỆN TẬP
B. Bài tập
1. Bài tập 1
Cách xác định hệ số b’ trong các trường hợp sau, trường hợp
nào đúng, trường hợp nào sai?
Sai

a. Phương trình 2x2 – 6x + 5 = 0 có hệ số b’ = 3

Đúng b. Phương trình 2x2 – 6x + 5 = 0 có hệ số b’ = – 3
Đúng c. Phương trình x2 – 4 3x + 5 = 0 có hệ số b’ = – 2
Đúng d. Phương trình – 3x2 +2(
Sai

2  1)

3

x + 5 = 0 có hệ số b’ =

e. Phương trình x2 – x – 2 = 0 có hệ số b’ = – 1

21

2. Bài tập 2

CỦNG CỐ VÀ LUYỆN TẬP

Giải phương trình x2 – 2x – 6 = 0 hai bạn Hoa và Minh làm như sau:

Bạn Minh giải:

Phương trình x – 2x – 6 = 0
(a = 1; b = – 2 ; c = – 6)
Ta có: Δ = (– 2)2 – 4.1.(– 6)
= 4 + 24 = 28
Do Δ = 28 > 0 nên phương trình có hai nghiệm phân biệt:
2

 (  2)  28 2  2 7

1  7
2.1
2
 (  2)  28 2  2 7
x2 

1  7
2.1
2
x1 

Bạn Hoa giải:

Phương trình x2 – 2x – 6 = 0
(a = 1; b’ = – 1 ; c = –6)
Ta có: Δ’ = (–1)2 –1.(–6)
=1+6=7
Do Δ’ = 7 > 0 nên phương trình có hai nghiệm phân biệt:

 (  1)  7
1  7
1
 (  1)  7
x2 
1  7
1
x1 

Bạn Giang bảo rằng: bạn Minh giải sai, bạn Hoa giải đúng. Cịn bạn An nói
cả hai bạn đều làm đúng.
Theo em: ai đúng, ai sai? Em chọn cách giải của bạn nào? Vì sao?


CỦNG CỐ VÀ LUYỆN TẬP
3. Bài tập 3
Trong các phương trình sau, phương trình nào nên dùng
cơng thức nghiệm thu gọn để giải ?
a. Phương trình 2x2 – 3x – 5 = 0
b. Phương trình x2 – 6x – 3 = 0
c. Phương trình – x2 + ( 2  1 ) x + 5 = 0
d. Phương trình x2 – x – 22= 0

* So sánh phần kiểm tra bài cũ với ví dụ 2 của bài (câu a, b), ta đã giải hai phương trình

a) 5x + 4x – 1 = 0
2

;

b) x 2  2 3x  3 0

* Theo em, phần bài giải nào tiện hơn? Ta nên dùng
công thức nghiệm hay cơng thức nghiệm thu gọn ?

* Có thể dùng cơng thức nghiệm thu gọn để giải
phương trình x2 + 3x – 4 = 0 được không?
* Vậy khi nào ta nên sử dụng công thức nghiệm
thu gọn để giải phương trình bậc hai một ẩn?


Phơng trình ax2 + bx + c = 0 (a 0)
Công thức nghiệm:
2


b
* Nếu 4ac
phơng trình có

Công thức nghiÖm thu gän:

b 2b ';  ' b '2  ac

hai nghiệm
phân
0 biệt:

*Nếu
phơng trình có
hai nghiệm
' phân
0 biệt:

b
b
x

;
x

* Nếu
ph
1
2 ơng trình có
2a
2a
nghiệm kép:
0

b ' '
b ' '

x

;
x

*Nếu
ph
1
2 ơng trình có
a
a
nghiệm kép:
' 0

* Nếu
ph
bơng trình vô
x1 x2
nghiệm.
2a

* Nếu
trình vô
ph
b ơng
'
x1 x2
nghiệm.
a

0

' 0


HƯỚNG DẪN VỀ NHÀ
1. Học thuộc:
- Công thức nghiệm thu gọn.
- Các bước giải phương trình bằng cơng thức
nghiệm thu gọn.
2. Vận dụng công thức nghiệm và công thức nghiệm
thu gọn vào giải bài tập:
Bài 17, 18, 20, 21 SGK để tiết sau luyện tập.



Xin chân thành cảm ơn các thầy cơ giáo
cùng tồn thể các em học sinh!