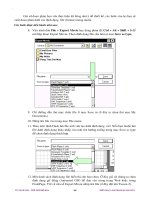
Hạt chuyễn động trong hố thế

18

Chơng III: Hạt chuyển động trong hố thế

3.1. Hạt chuyển động trong hố thế
a) Hàm riêng và trị riêng
Ta đ biết rằng đối với hạt chuyển động tự do thì phổ trị riêng
của toán tử năng lợng là liên tục
m
k
E
2
22
h
=
và các hàm riêng tơng
ứng là
( )
ikx
k
Aex =

.
Bây giờ ta hy xét trờng hợp hạt chuyển động trong hố thế
một chiều
=
)(
xV
khi
0
x

hoặc
Lx
(miền 1);
0)(
=xV
khi
Lx <<
0
(miền 2).
Trong miền 1: Với
E
hữu hạn:

EH =
1


Do

,
E
hữu hạn nên vế phải hữu hạn, suy ra
0
=

;
0
2
=

ở miền 1.
Trong miền 2:
( ) ( )
xEx
xm
nnn

=



2
22
2
h
.
Điều kiện biên:
( ) ( )
00
== L
nn

.
Đặt
2
2
2
h
n
n

mE
k =
, ta có nghiệm
( )
xkBxkAx
nnn
cossin
+=

.
Từ điều kiện biên suy ra
19

0
=B
;
0sin
=LkA
n
hay

nLk
n
=
;
2,1,0
=
n
.
Vậy phổ trị riêng và hàm riêng rời rạc.

Từ điều kiện chuẩn hoá
( )

=
L
n
dxx
0
2
1

ta có
L
A
2
=
.
Vậy hàm riêng và trị riêng của hạt chuyển động trong hố thế đ
nêu là
( )






=
L
xn
L

x
n


sin
2
;
1
2
EnE
n
=
;
2
22
2
1
2
1
2
2
mL
m
k
E

h
h
==
.

Ta thấy rằng khi
0=n
thì
0=

, do đó
0
2
=

, hạt không tồn tại
ở trạng thái
0
=n
.

b) Thừa số pha tuỳ ý
Ta đ biết rằng hàm sóng

cho thông tin về hệ:

= dxCC


*
.
Điều kiện chuẩn hoá của hàm sóng là

= 1
*

dx

.
Giá trị của các biểu thức nói trên không thay đổi dới tác dụng
của phép biến đổi



i
e
, trong đó

là số thực.
Nh vậy hàm sóng đợc xác định chính xác đến một thừa số
pha

i
e
. Đại lợng tuỳ ý này không ảnh hởng tới bất cứ kết quả vật
lí nào.

3.2. Kí hiệu Dirac
20
Trong Cơ học lợng tử, ngoài kí hiệu tích phân thông thờng,
ta còn dùng kí hiệu Dirac.
Khi gặp kí hiệu

, ta phải hiểu nh sau
1) lấy liên hợp phức của đối tợng trong khe thứ nhất:
*

;
2) lấy tích phân của tích

*
.
Các tính chất:
Nếu
a
là số phức,

và

là 2 hàm sao cho

+

<dx


thì
a)

aa =
;
b)

*
aa =

;
c)

=
*
;
d)
( )( )
2121

++
=
11

+
21

+
12

+
22

.

3.3. Nguyên lí chồng chập
Trở lại bài toán hố thế một chiều.
Ta hy tởng tợng một số lớn các phép lặp đồng nhất của hệ.
Tất cả các hố thế ở cùng trạng thái ban đầu
( )

0,x

.
Sau khoảng thời gian
t
, tất cả các hố thế ở cùng trạng thái
( )
tx,

.
Năng lợng của hạt trong mỗi hố thế ở thời điểm
t
bằng bao
nhiêu?
21
Điều đặc biệt là: năng lợng đo trong các hố thế giống nhau, ở
cùng trạng thái
( )
tx
,

, không nh nhau!
Các câu hỏi thích hợp hơn có thể đặt ra là:
1) Năng lợng trung bình đo đợc trong tất cả các hố thế là bao
nhiêu?
2) Nếu ta đo năng lợng trong một hố thế thì xác suất đo đợc
một giá trị cụ thể, ví dụ
3
E
, là bao nhiêu?

Nếu xác suất tìm thấy giá trị
n
E
trong một phép đo năng lợng
là
( )
n
EP
thì năng lợng trung bình của tất cả các phép đo của tất cả
các thành viên của tập hợp là
( )
n
E
n
EEPE
n


=
. (1)
Công thức (1) đúng cho mọi đại lợng vật lí. Ví dụ:

=
L
dxxxPx
0
)(
. (2)
Theo tiên đề 3:

HE

=
. (3)
Ta hy khai triển trạng thái

theo các hàm riêng của
H

. Các
hàm riêng thoả mn phơng trình trị riêng
nnn
EH

=

. (4)
Đối với bài toán hố thế sâu vô hạn thì
( )






=
L
xn
L
x

n


sin
2
. (5)
Khai triển

theo các hàm riêng
n


( ) ( ) ( )


=
=
1
,
n
nn
xtbtx

. (6)
22
Nếu viết theo kí hiệu Dirac, ta có


=
=

1n
nn
b

. (7)
Thay (7) vào (3) ta có

=
l
ll
n
nn
bHbE


=
ln
l
ln
n
Hbb


*

=
lnl
l
ln
n

Ebb


*
=
nll
l
ln
n
Ebb


*
=


=1
2
n
nn
Eb
. (8)
So sánh (8) và (1) ta đợc


=1
2
n
nn
Eb

=
( )
n
n
n
EEP

. (9)
Vậy
2
n
b
chính là xác suất để ở thời điểm
t
phép đo năng lợng
của hạt ở trạng thái
( )
tx
,

thu đợc giá trị
n
E
:
( )
n
EP
=
2
n

b
. (10)
Nếu

và
n

đ chuẩn hoá thì các hệ số cũng đợc chuẩn hoá.
Thật vậy:

=
1
=

l
ll
n
nn
bb

=
ln
l
ln
n
bb


*

=
nl
l
ln
n
bb


*
=

=
1
2
n
n
b
, (11)
tức là
2
n
b
là xác suất tuyệt đối.
Nếu

và
n

cha chuẩn hoá thì
( )

n
EP
=

22
22
nn
nn
cb
cb
=

22
nn
cb
, (12)
2
n
c
=
nn

.