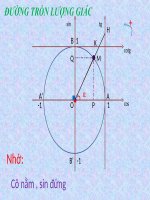
Bổ trợ lượng giác (công thức biến đổi)

CÔNG THỨC LƯỢNG GIÁC
1.Công thức cộng:
( )
1 .
tga tgb
tg a b
tga tgb
+
+ =
−
cos(a+b) = cosacosb - sinasinb
cos(a-b) = cosacosb +
sinasinb
sin(a+b) = sinacosb + sinbcosa
sin(a-b) = sinacosb – sinbcosa
( )
1 .
tga tgb
tg a b
tga tgb
−
− =
+
Nhớ :
cos thời cos cos, sin sin
sin thời sin cos, cos sin là cùng
tg tổng thì tổng tg ta
phép chia của một trừ thừa tg ra
Cụ thể : VT và VP ngược dấu
VT và VP cùng dấu
( )

1 .
tg tg
tg
tg tg
+
+ =
−
tg hiệu là hiệu tg ngươi
phép chia của một cộng thừa tg vô
( )
1 .
tg tg
tg
tg tg
−
− =
+
cos
cotg
tg
O
+
-1
-1
1
1
B
AA’
B’
M

P
Q
sin
K
α
N
E
F
β
Vận dụng kiến thức đã học :
( )
. . .cos ;u v u v u v=
r r r r r r
. .u p i q j= +
r r r
1i j= =
r r
( )
; 2ON OM k
α β π
= − +
uuur uuuur
j
r
i
r
0
1
x
y

1
( )
1;0i
r
( )
0;1j
r
( ; )u p q=
r
2 2
u p q= +
r
( )
;v a b=
r
. . .u v p a q b= +
r r
Xét M , N trên mp tọa độ Oxy :
x
y
( )
cos ;sinOM
β β
=
uuuur
( )
cos ;sinON
α β
=
uuur

( )
. . .cos ;OM ON OM ON OM ON=
uuuur uuur uuuur uuur uuuur uuur
( )
cos cos sin sin 1. 1.cos 2k
α β α β α β π
+ = − +
 
 
cos cos sin sin
α β α β
+ =
2 2 2 2
cos sin . cos sin .
α α β β
+ +
( )
cos 2k
α β π
− +
( )
cos cos sin sin cos
α β α β α β
+ = −
( )
cos
α β
+ =
( )
cos

α β
− − =
 
 
( )
cos cos cos sin sin
α β α β α β
+ = −
( ) ( )
cos cos sin sin
α β α β
− + −
( )
( )
( )
sin
sin cos sin cos
cos cos cos sin sin
tg
α β
α β β α
α β
α β α β α β
+
+
+ = =
+ −
sin cos sin cos
cos cos cos cos
cos cos sin sin

cos cos cos cos
α β β α
α β α β
α β α β
α β α β
+
=
−
sin sin
cos cos
sin sin
1 .
cos cos
α β
α β
α β
α β
+
=
−
1
tg tg
tg tg
α β
α β
+
=
−
( )
1

tg tg
tg
tg tg
α β
α β
α β
+
+ =
−
( ) ( )
tg tg
α β α β
− = + − = 
 
( )
( )
1
tg tg
tg tg
α β
α β
+ −
=
− −
1
tg tg
tg tg
α β
α β
−

+
Đối với cotg(α±β) vận dụng tg(α±β) vào và nhớ cotg bằng
nghịch đảo của tg
Ví dụ : Tính cos150 và cotg2150
0
cos15 =
( )
0 0
cos 45 30− =
0 0 0 0
cos 45 cos30 sin 45 sin 30+
2 0 2 0
sin 15 1 cos 15= −
( )
2
4 2 2
6 2 8 4 2 2 2
1 1 1
4 16 4 4
− +
 
+ + +
= − = − = − =
 ÷
 ÷
 
2 0
2 2
sin 15
4

−
=
0
2 2 2 2
sin15
4 2
− −
= =
2 0
2 0
1
15 1
sin 15
cotg = −
( )
4 2 2
1 4 2 2 2 1
1 1
2 2 2 2 2 2 2 2 2 1
4
− −
+ +
= − = − = = =
− − − − −
Giải
Ví dụ : Tính
sin
8
π
2 2

cos cos sin
4 8 8
π π π
= −
2 2
1 sin sin
8 8
π π
 
= − −
 ÷
 
2
cos 1 2sin
4 8
π π
= −
2
1 cos
2 2 2 2
4
sin sin
8 2 4 8 2
π
π π
−
− −
= = =
2 2
sin

8 2
π
−
=
cos cos cos sin sin
8 8 8 8 8 8
π π π π π π
 
+ = −
 ÷
 
Giải
2. Công thức nhân đôi :
sin2α = 2sinαcosα
cos2α = cos2α – sin2α
= 2cos2α – 1
= 1 – 2sin2α
2
2
2
1
tg
tg
tg
α
α
α
=
−
Nhớ :

sin cặp thì cặp sin cô
cos hai lấy hiệu bình cô sin bình
thêm hai cos bình trừ duy nhất
duy nhất trừ đi hai sin bình
tg nhị là nhị tg anh
phép chia của một trừ bình tg thôi
Chứng minh : Vận dụng các công thức sin(α+β), cos(α+β)
và tg(α+β). Cụ thể :
cos 2
α
=
cos( )
α α
+ =
cos cos sin sin
α α α α
− =
2 2
cos sin
α α
−
sin 2
α
=
sin( )
α α
+ =
sin cos sin cos
α α α α
+ =

2sin cos
α α
2
2
2
1 1
tg tg tg
tg
tg tg tg
α α α
α
α α α
+
= =
− −
a. Hệ quả 1:
2
2
2
1 cos 2
cos
2
1 cos2
sin
2
1 cos2
1 cos2
tg
α
α

α
α
α
α
α
+
=
−
=
−
=
+
Các công thức sau đây cho
phép tính cosα, sinα và tgα
theo
, 2
2
t tg k
α
α π π
= ≠ +
2
2
2
2
2
sin
1
1
cos

1
2
1
t
t
t
t
t
tg
t
α
α
α
=
+
−
=
+
=
−
Chứng minh :
Chứng minh :
Vận dụng các công thức nhân
đôi ta được hệ qủa một.
b. Hệ quả 2:
cos bình không biết bằng chi ?
mẫu hai, tử tổng một và cos hai
Nhớ :