Tuan 28-Hinh 8-Tiet 48 CAC TRUONG HOP DONG DANG CUA TAM GIAC VUONG -Yen
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (168.6 KB, 8 trang )
<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>
<b>CHÀO MỪNG CÁC THẦY CÔ</b>
<b>ĐẾN DỰ GIỜ THĂM LỚP</b>
</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>
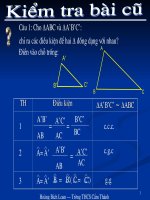
<b>KIỂM TRA BÀI CŨ</b>
Bài 1: Cho tam giác ABC vuông ở A,
đường cao AH. Chứng minh:
)
)
<i>a ABC</i> <i>HBA</i>
<i>b ABC</i> <i>HAC</i>
<b>∽</b>
<b>∽</b>
Bài 2: Cho hình vẽ. Tam gác ABC có
đồng dạng với tam giác DEF khơng?
Vì sao?
Giải:
a) <i>ABC v</i> à <i>HBA</i> có
<sub>90 ( ); </sub>0
<i>A H</i> <i>gt B chung</i>
( )
<i>ABC</i> <i>HBA g g</i>
<b>∽</b>
à có
<i>ABC v</i> <i>HAC</i>
<i><sub>A H</sub></i> <sub>90 ( ); </sub>0 <i><sub>gt C chung</sub></i>
( )
<i>ABC</i> <i>HAC g g</i>
<b>∽</b>
b)
Giải:
0
à EF có
90 ( )
8
2
4
6
2
3
EF ( )
<i>ABC v</i> <i>D</i>
<i>A D</i> <i>gt</i>
<i>AB</i>
<i>AB</i> <i>AC</i>
<i>DE</i>
<i>AC</i> <i>DE</i> <i>DF</i>
<i>DF</i>
<i>ABC</i> <i>D</i> <i>c g c</i>
</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>
Tiết 48:
<b>§8. CÁC TRƯỜNG HỢP ĐỒNG DẠNG </b>
<b>CỦA TAM GIÁC VUÔNG</b>
LTV
<b>1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông</b>
<b>2. Dấu hiệu nhận biết hai tam giác vuông đồng dạng</b>
? Hãy chỉ ra các tam giác vuông đồng dạng trong hình sau.
Giải:
0
0
2 2 2
2 2
0
2 2 2
2 2
) EF ' ' ' ì
' 90
1
' ' ' ' 2
) ' ' '; ' 90 ê
' ' ' ' ' '
5 2 21 ' ' 21
; 90 ê
10 4 84 84 2 21
' ' 2 1
4 2 ' ' ' '
' ' 21 1
2
2 21
' ' ' (
<i>D</i> <i>D E F v</i>
<i>D</i> <i>D</i>
<i>DE</i> <i>DF</i>
<i>D E</i> <i>D F</i>
<i>A B C A</i> <i>n n</i>
<i>A C</i> <i>B C</i> <i>A B</i>
<i>A C</i>
<i>ABC A</i> <i>n n</i>
<i>AC</i> <i>BC</i> <i>AB</i>
<i>AC</i>
<i>A B</i>
<i>AB</i> <i>A B</i> <i>A C</i>
<i>AB</i> <i>AC</i>
<i>A C</i>
<i>AC</i>
<i>A B C</i> <i>ABC c</i>
<sub></sub>
<b>∽</b>
</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>
Tiết 48:
<b>§8. CÁC TRƯỜNG HỢP ĐỒNG DẠNG </b>
<b>CỦA TAM GIÁC VUÔNG</b>
<b>1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông</b>
<b>2. Dấu hiệu nhận biết hai tam giác vuông đồng dạng</b>
Định lý 1
0
; ' ' '; ' 90
' ' ' '
(1)
<i>ABC A B C A A</i>
<i>B C</i> <i>A B</i>
<i>BC</i> <i>AB</i>
' ' '
<i>A B C</i> <i>ABC</i>
<b>∽</b>
2 2
2 2
' ' ' '
<i>B C</i> <i>A B</i>
<i>BC</i> <i>AB</i>
GT
KL
<i><b>Chứng minh:</b></i> Từ (1) bình phương hai vế ta được:
Theo t/c của dãy tỷ số bằng nhau, ta có:
Ta có: 2 2 2
2 2 2
' ' ' ' ' '
( )
<i>B C</i> <i>A B</i> <i>A C</i>
<i>BC</i> <i>AB</i> <i>AC Py ta go</i>
Do đó:
Vậy <i>A B C</i>' ' '<b>∽</b> <i>ABC</i> (trường hợp đồng dạng thứ nhất)
2 2 2 2
2 2 2 2
' ' ' ' ' ' ' '
<i>B C</i> <i>A B</i> <i>B C</i> <i>A B</i>
<i>BC</i> <i>AB</i> <i>BC</i> <i>AB</i>
2 2 2
2 2 2
' ' ' ' ' ' ' ' ' ' ' '
<i>B C</i> <i>A B</i> <i>A C</i> <i>B C</i> <i>A B</i> <i>A C</i>
</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>
Tiết 48:
<b>§8. CÁC TRƯỜNG HỢP ĐỒNG DẠNG </b>
<b>CỦA TAM GIÁC VUÔNG</b>
LTV
<b>1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông</b>
<b>2. Dấu hiệu nhận biết hai tam giác vuông đồng dạng</b>
<b>3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giac đồng dạng</b>
Định lý 2
GT
KL
' '
' ' ' ;
' ' ' ';
<i>A B</i>
<i>A B C</i> <i>ABC</i> <i>k</i>
<i>AB</i>
<i>A H</i> <i>B C AH</i> <i>BC</i>
<b>∽</b>
' ' ' '
<i>A H</i> <i>A B</i>
<i>k</i>
<i>AH</i> <i>AB</i>
' '
' ' ' ( ) ' , à <i>A B</i>
<i>A B C</i> <i>ABC GT</i> <i>B</i> <i>B v</i> <i>k</i>
<i>AB</i>
<b>∽</b>
0
ét ' ' ' à ó ' 90 ; ' ( )
' ' ' '
' ' '
<i>X</i> <i>A B H v</i> <i>ABH c H</i> <i>H</i> <i>B</i> <i>B cmt</i>
<i>A H</i> <i>A B</i>
<i>A B H</i> <i>ABH</i> <i>k</i>
<i>AH</i> <i>AB</i>
<b>∽</b>
</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>
Tiết 48:
<b>§8. CÁC TRƯỜNG HỢP ĐỒNG DẠNG </b>
<b>CỦA TAM GIÁC VUÔNG</b>
<b>1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông</b>
<b>2. Dấu hiệu nhận biết hai tam giác vuông đồng dạng</b>
<b>3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giac đồng dạng</b>
Định lý 3
GT
KL
' '
' ' ' ;
' ' ' ';
<i>A B</i>
<i>A B C</i> <i>ABC</i> <i>k</i>
<i>AB</i>
<i>A H</i> <i>B C AH</i> <i>BC</i>
<b>∽</b>
2
' ' '
<i>A B C</i>
<i>ABC</i>
<i>S</i>
<i>k</i>
<i>S</i>
<i>Chứng minh:</i>
2
' ' '
1
' '. ' ' <sub>' '</sub> <sub>' '</sub>
2 <sub>.</sub> <sub>.</sub>
1
.
2
<i>A B C</i>
<i>ABC</i>
<i>A H B C</i>
<i>S</i> <i>A H B C</i>
<i>k k k</i>
</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>
Tiết 48:
<b>§8. CÁC TRƯỜNG HỢP ĐỒNG DẠNG </b>
<b>CỦA TAM GIÁC VUÔNG</b>
LTV
Bài 46/sgk-84
Hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ
tự các đỉnh tương ướng giải thích vì sao chúng đồng dạng?
Giải:
, , , .
<i>ABE ADC FDE FBC</i>
1 2
1) (1) ( chung)
2) (2) ( chung)
3) (3) ( chung)
4) ( )
5) (1) và (2)
6) (1) và (3)
<i>ABE</i> <i>ADC</i> <i>A</i>
<i>ABE</i> <i>FDE</i> <i>E</i>
<i>ADC</i> <i>FBC</i> <i>C</i>
<i>FDE</i> <i>FBC F</i> <i>F</i>
<i>ADC</i> <i>FDE</i>
<i>ABE</i> <i>FBC</i>
<b>∽</b>
<b>∽</b>
<b>∽</b>
<b>∽</b>
<b>∽</b>
<b>∽</b>
Trong hình có 4 tam giác vng là:
</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>
HƯỚNG DẪN VỀ NHÀ
- Học bài nắm vững trường hợp đồng dạng của tam giác vuông,
nhất là trường hợp đồng dạng đặc biệt ( cạnh huyền, cạnh góc
vng tương ứng tỷ lệ), tỷ số hai đường cao tương ứng, tỷ số diện
tích của hai tam giác đồng dạng.
</div>
<!--links-->