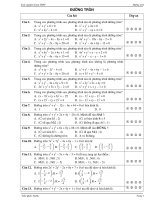
Trắc nghiệm đường tròn 10 Nguyễn Thế Thu

Trắc nghiệm Hình giải tích
ðƯỜNG TRÒN

Câu 1:
ðường tròn
2 2
( ): 2 2 1 0C x y x y+ − + − = có tâm là
I.
( 2; 1)I − II.
1
( 2; )
2
I
III.
1
( 2; )
2
I −
IV.
1
( 2; )
2
−

Câu 2:
ðiểm
(2;1)I
là tâm của ñường tròn nào sau ñây
2 2
. 4 2 1 0x y x y+ + + + =
I II.

2 2
5
3 3 12 6 0
7
x y x y+ − − + =

III.
2 2
4 2 1 0x y x y+ − + − =
IV.
2 2
4 2 3 0x y x y+ + − − =

Câu 3:
ðường tròn
2 2
( ):8 8 8 4 1 0C x y x y+ − + − =
có bán kính là
I.
21R = II.
11
2
R = III.
7
4
R = IV. Kết quả khác
Câu 4: Trong các ñường tròn sau, ñường tròn nào có bán kính lớn nhất
I.
2 2
2 2 1 0x y x+ − − = II.

2 2
1
0
3
x y x y+ − + − =
III.
2 2
4 3 2 0x y x y+ + − − = IV.
2 2
3 3 12 19 2 0x y x y+ − + − =
Câu 5:
ðường tròn
( ):2 2 3 4 2 0C x y x y+ − + + = có:
I. Tâm
3
( ; 2)
2
I − và bán kính
11
2
R = II. Tâm
3
( ; 1)
4
I − và bán kính
3
16
R =
III. Tâm
3

( ;1)
4
I − và bán kính
3
4
R = IV. Tâm
3
( ; 1)
4
I − và bán kính
3
4
R =
Câu 6: Phương trình nào sau ñây là phương trình ñường tròn
2 2 2 2
2 2 2 2
. 2 1 0 . 2 4 1 0
. 2 2 2 3 3 5 0 . 2 3 0
x y xy y x y x y
x y x y x y x y
+ − + − = − − + − =
+ − + + − = + − + + =
I II
III IV

Câu 7: ðường tròn tâm
(1;2)I
, bán kính
1R =
có phương trình là

I.
2 2
( 1) ( 2) 1 0x y+ + − − =
II.
2 2
2 4 4 0x y x y+ − − + =

III.
2 2
( 1) ( 2) 1x y− + + =
IV.
2 2
2 4 1 0x y x y+ − − − =

Câu 8:
Cho
(1;2), ( 5;4), ( 1;6)A B C− −
.
a) Ph
ương trình ñường tròn ñường kính AC là:
I.
2 2
( 4) 5x y+ − =
II.
2 2
4 6 3 0x y x y+ + − + =

III.
2 2
8 10x y x+ − −

IV.
2 2
4 8 3 0x y x y+ + + + =

b) ðường tròn tâm A ñi qua B có phương trình là
I.
2 2
2 4 35 0x y x y+ − − − =
II.
2 2
2 4 45 0x y x y+ − − − =

III.
2 2
( 1) ( 2) 40x y+ + + =
IV.
2 2
( 1) ( 2) 10x y− + − =

c) ðường tròn ngoại tiếp tam giác ABC có phương trình là
Trắc nghiệm Hình giải tích
I.
2 2
4 6 3 0x y x y+ + − + =
II.
2 2
( 2) ( 3) 5x y− + − =
III.
2 2
( 2) ( 3) 40x y+ + − =

IV.
2 2
4 6 3 0x y x y+ + + − =

Câu 9
: ðường tròn tâm
(2;3)I
và tiếp xúc với ñường thẳng
3 4 1 0x y+ − =
có bán kính
I.
17
5
R =
II.
289
25
R =
III.
17
25
R =
IV.
289
5
R =

Câu 10: Các ñường thẳng sau ñường thẳng nào tiếp xúc với ñường tròn:
2 2
( 1) ( 1) 1x y− + − =

I.
1 0x y+ + =
II.
2 0y − =
III.
2 0x + =
IV.
4 3 9 0x y− + =

Câu 11:
Trong các ñường tròn sau ñường tròn nào tiếp xúc với ñ/t:
4 3 2 0x y+ − =

I.
2 2
2 2 1 0x y x y+ − − + =
II.
2 2
( 3) ( 1) 1x y− + + =

III.
2 2
( 1) 1x y+ − =
IV.
2 2
( 1) 1x y− + =

Câu 12:
Tiếp tuyến của ñường tròn

2 2
( ):( 1) ( 2) 1C x y− + − =
tại
(2;2)M
có phương trình:
I.
2 2 0x y− + =
II.
2 2 0x y− − =
III.
2 0y − =
IV.
2 0x − =

Câu 13:
Phương trình nào sau ñây là phương trình ñường tròn ?
I.
2 2
2 0x y+ + =
II.
2 2
+4 4x y =

III.
2 2
4 2 3 0x y xy y+ − + − =
IV.
2 2
4 0x y x+ + =

Câu 14: Phương trình nào sau ñây không phải là phương trình ñường tròn ?
I. x
2
+ y
2
– 4x + 2y + 2 = 0 II. x
2
+ y
2
– 4mx + 2y + m = 0
III. 2x
2
+ 2y
2
– 4x + 2y – 3 = 0 IV. x
2
+ y
2
+ 4x – 2y + 7 = 0
Câu 15:
ðường tròn ñi qua ñiểm M(2; 1) và tiếp xúc với trục hoành tại ñiểm (1; 0) có phương
trình?
I. (x – 1)
2
+ (y – 1)
2
= 1 II. (x – 2)
2
+ (y – 2)
2

= 1
III. (x – 1)
2
+ (y + 1)
2
= 5 IV. (x + 5)
2
+ (y + 5)
2
= 25
Câu 16: Ph
ương trình trục ñẳng phương của hai ñường tròn : x
2
+ y
2
+ 2x – y + 1 = 0 và
x
2
+ y
2
– 6x – 2y + 1 = 0 là :
I. 8x + y = 0 II. 8x + y + 2 = 0 III. –4x – 3y + 2 = 0 IV. 8x – y = 0
Câu 17:
ðể phương trình x
2
+ y
2
+ 2(2m – 3)x – (2m + 2)y + 4m
2
– 4m + 2 = 0 là phương

trình c
ủa một ñường tròn thì giá trị của m phải là :
I.
2 4m< <
II.
2m <
hoặc
4m >
III. m = –2 hay m = –4 IV. m<–4 hay m > –2
Câu 18:
ðường tròn tâm I(4; –2) tiếp xúc với trục hoành có phương trình là :
I. (x – 4)
2
+ (y + 2)
2
= 16 II. (x + 4)
2
+ (y – 2)
2
= 4
III. (x – 4)
2
+ (y + 2)
2
= 2 IV. (x – 4)
2
+ (y + 2)
2
= 4
Câu 19:

ðường tròn tâm I(2; –1), bán kính R = 3 có phương trình là :
I. x
2
+ y
2
+ 4x – 2y = 0 II. x
2
+ y
2
– 4x – 2y + 9 = 0
III. x
2
+ y
2
– 4x + 2y – 4 = 0 IV. x
2
+ y
2
– 4x + 2y + 4 = 0
Câu 20: ðiểm O nằm bên trong ñường tròn : x
2
+ y
2
– 6x + 4y + m(m – 4) = 0 thì tham số m
ph
ải thỏa ñiều kiện :
I. 0 < m < 4 II. m < 0 ho
ặc m > 4 III. m = 0 hoặc m = 4 IV. m ≤ 0 hoặc m ≥ 4
Trắc nghiệm Hình giải tích
Câu 21: Phương tích của ñiểm M(–1; 3) ñối với ñường tròn ñường kính AB với A(1; 4) và

B(5; –2) là :
I. 33 II. 20 III. –7 IV. 7
Câu 22: Ti
ếp tuyến của ñường tròn x
2
+ y
2
– 4x + 2 = 0 tại ñiểm M(1; –1) có phương trình là :
I. x – y – 2 = 0 II. x + y = 0 III. –x – y + 4 = 0 IV. –x – y – 4 = 0
Câu 23: Các ph
ương trình sau, ñâu không là phương trình ñường tròn
2 2 2 2
2 2 2 2
. 4 6 5 0 . 4 4 2 2 1 0
. 3 5 1 0 . 5 5 3 4 1 0
x y x y x y x y
x y x y x y x y
+ + − − = + + − + =
+ + + + = + − + + =
I II
III IV

Câu 24: ðường tròn (C):
2 2
4 2 4 0x y x y+ − + − = có tâm là
. (2; 1) . ( 2; 1) . (2;1) . (1;2)I I I I− − −I II III IV

Câu 25:
ðường tròn (C):
2 2

16 16 16 8 11 0x y x y+ + − − =
có bán kính là
12 4
. . . 1
. 2
9 5
R R R R= = = =I II III IV
V. Một ñáp án khác
Câu 26: Tìm m ñể phương trình
2 2
2 2 0x y mx+ − + =
là phương trình ñường tròn
0 0
. . . 2 . 0
2 2
m m
m m
m m
< ≤
 
≥ >
 
> ≥
 
I II III IV
V. ðáp án khác
Câu 27:
ðường tròn ñường kính AB với A(1;1), B(7;5) có phương trình là
2 2 2 2
2 2 2 2

. ( 4) ( 3) 13 . ( 4) ( 3) 13
. 8 6 12 0 . 8 6 1
0 0
x y x y
x y x y x y x y
+ + − = − + + =
+ − − + = + + + + =
I II
III IV

Câu 28: Ph
ương trình ñường ñường tròn ñi qua A(2;-3) có tâm I(-2;3) là
2 2 2 2
2 2 2 2
. 4 6 39 0 . 4 6 2 0
. 4 6 23 0 . 4 6 1 0
x y x y x y x y
x y x y x y x y
+ + − − = + + + + =
+ − − − = + − + + =
I II
III IV

Câu 29: ðường tròn có tâm I(-1;2) và tiếp xúc với ñ/t
: 2 7 0d x y− + =
có p/trình là
2 2 2 2
2 2 2 2
4 4
. ( 1) ( 3) . ( 1) ( 2) 0

7 5
. 5 5 10 20 21 0 . 4 4 8 16 11 0
x y x y
x y x y x y x y
+ + − = + + − + =
+ + − + = + + − + =
I II
III IV

Câu 30: Ph
ương trình ñường tròn ñi qua ba ñiểm
(1;2), (5;2), (1; 3)A B C −
là
2 2 2 2
2 2 2 2
. 6 1 0 . 6 1 0
. 6 1 0 . 6 1 0
x y x y x y x y
x y x y x y x y
+ − + − = + + + + =
+ + + + = + − + − =
I II
III IV

Câu 31: Tìm m ñể ñường thẳng (d):
( 1) 0 m x y m− − − =
tiếp xúc với ñường tròn có phương
trình
2 2
4 4 7 0x y x y+ − + + =

. 2 . 1 . 1 2 . 0m m m và m m= = − = − = =I II III IV
V. Một ñáp án khác
Câu 32: Ti
ếp tuyến của ñường tròn (C):
2 2
4 8 5 0x y x y+ − + − =
tại A(-1;0) là
. 3 4 3 0 . 4 3 3 0 . 3 4 3 0 . 4 3 3 0x y x y x y x y+ + = − + = − + = + + =I II III IV

Trắc nghiệm Hình giải tích
Câu 33: Phương trình tiếp tuyến của ñường tròn (C):
2 2
4 8 5 0x y x y+ − + − =
song song với
ñường thẳng
4 3 1 0x y+ + =
là
. 4 3 29 0 . 4 3 21 0 . 3 4 29 0 . 3 4 21 0x y x y x y x y+ + = + + = − + = − − =I II III IV

Câu 34: Qua A(1;5) có bao nhiêu ti
ếp tuyến kẻ ñến ñường tròn: (x-1)
2
+(y+1)
2
=1
I. 1 II. 2 III. 3 IV. Không có tiếp tuyến nào
Câu 35: Ti
ếp tuyến của ñường tròn
2 2

( 1) ( 2) 9x y+ + − =
ñi qua M(2;-1) là
I.
1 0x y+ + =
và
2 0x y− + =
II.
1 0x + =
và
2 0y + =

III.
2x =
và
1y = −
IV.
2 1 0x y+ + =