Bài soạn ứng dụng tích phân

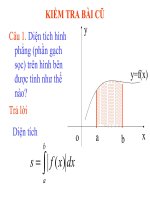
KIỂM TRA BÀI CŨ
? Em hãy nêu công thức và cách tính diện tích phần hình
phẳng giới hạn bởi hai đồ thị y = f(x) và y = g(x) liên tục trên
đoạn [a; b] và hai đường thẳng x = a ; x = b
y = f (x)

y = g (x)
y = f (x)

y = g (x)

b

S = ∫ f ( x) − g ( x) .dx
a


KIỂM TRA BÀI CŨ

y= x

? Em hãy tính diện
tích phần gạch sọc ?
2

S = ∫ x .dx
0

? Bây giờ ta cho đường cong
3
2 trục Ox em sẽ

2=4 2
2
quay = ( x )
S quanh
được một khối trịn xoay ?
0
3
3
Hãy tính thể tích khối trịn
xoay đó?

? Tính diện tích các khối trịn xoay ?


Người ta tính được lưu lượng dịng chảy như thế nào ?
Người ta tính thể tích của một con tàu như thế nào ?



Nhắc lại cơng
thức tính thể tích
của một số khối
trong khơng gian


Bài 6:
THỂ TÍCH VẬT THỂ TRỊN XOAY
I. Tính thể tích của một vật thể.
Bài tốn:
I.1. Thể tích khối chóp cụt.

I.2. Thể tích khối chóp .

II. Thể tích khối trịn xoay
II.1. Khối chỏm cầu.
II.2. Khối nón cụt
II.3. Khối nón.
II.4. Khối trụ


1. Thể tích của một vật thể

Cho vật thể trong không
gian Oxyz. Gọi B là phần
vật thể bị giới hạn bởi hai
mặt phẳng vng góc với
trục Ox tại các điểm a, b
như hình vẽ

x

Gọi S(x) là diện tích thiết
diện của vật thể bị cắt bởi
mặt phẳng vng góc với
trục Ox tại điểm x ∈[a; b]

a

b

Giả sử S(x) là một hàm

liên tục trên đoạn [a; b]
Thể tích của vật thể là:

b

V = ∫ S ( x)dx
a


Thể tích khối chóp cụt.

h: chiều cao.
S0: diện tích đáy nhỏ
S1: diện tích đáy lớn

S1

S0

O

a

V: thể tích khối chóp
cụt

b

1
V = ∫ S ( x ) dx = h.( S 0 + S 0 S1 + S )

a
3
b

1

cơng thức tính thể tích khối chóp có chiều cao h , diện tích đáy B:

1
V = h.B
3

( do S 0 = 0)


Đặt khối chóp (sinh ra khối chóp cụt) có đường cao trùng với trục
Ox và đỉnh trùng với gốc O.
S(x): thiết diện
tại điểm có
hồnh độ x thuộc
đoạn [a; b] vng
góc với trục Ox.
S1
S
x

O

a

a

b

x

b
S ( x)
x2
= 2
S1
b

Theo tính chất đồng dạng ta ln có:
b

S 0 = S (a )
với
a2
x
1
= S1 . 2
= ∫S
dx = h.( S + S S + S )
b
b
3

V = ∫ S ( x ) dx
a

2

b

1

a

2

0

0

1

1


2. Thể tích khối trịn xoay:
Cho hàm số y = f(x) liên tục, và khơng âm trên đoạn [a; b].
Hình phẳng giới hạn bởi đồ thị hàm y = f(x), trục Ox, và hai đường
thẳng x =a; x= b khi quay quanh trục Ox tạo nên một khối tròn xoay.

Thể tích của khối trịn xoay
được tính theo cơng thức:
b

V = π ∫ f ( x).dx

a

2


Thể tích khối chỏm cầu
Trong mặt phẳng Oxy, xét hình phẳng giới hạn bởi cung trịn tâm O
bán kính R có phương trình
y = R 2 − x 2 , trục hoành và đường
thẳng x = R – h (0 < h ≤ R). Quay hình phẳng đó quanh trục Ox ta thu
được khối chỏm cầu bán kính R, chiều cao h.

y = R2 − x2

h
V = πh .( R − )
3
2

h
O

R-h

Thể tích của khối chỏm cầu
được tính theo cơng thức:

R

Chứng minh:
Thể tích của khối chỏm cầu:
b

R

V = π ∫ f ( x).dx = π ∫ ( R − x ).dx
2

2

2

R −h

a

3

x R
h
2
= π ( R x − ) R −h = πh ( R − )
3
3
2

? Em hãy nêu cơng thức tính thể tích khối cầu bán kính R ?

? h = ….....

4 3
V = πR
3


Tính thể tích khối trịn xoay tạo thành khi hình
phẳng giới hạn bởi đồ thị hàm số y = x2, Ox và các
đường thẳng x = 1, x = 2 khi quay quanh Ox
y = x2

Thể tích của khối
trịn xoay tạo bởi đường cong y
= x2, Ox và các đường thẳng x
= 1, x = 2 khi đường cong này
quay quanh Ox được tính theo
cơng thức:
b

V = π ∫ f 2 ( x).dx
a

2

= π ∫ ( x ) .dx
2 2

1

Tương tự
Cho đường cong có phương trình x = g(y), trong
đó g là hàm số liên tục và khơng âm trên đoạn [c; d].
Hình phẳng giới hạn bởi đường cong x = g(y) , trục
tung và hai đường thẳng y = c, y = d, quay quanh trục tung
tạo nên một khối trịn xoay.
Thể tích của khối
trịn xoay được tính
theo công thức:
d

V = π ∫ g 2 ( y ).dx
c


Thể tích khối nón cụt
Cho khối nón cụt có chiều cao h, bán kính đáy lớn
và đáy nhỏ lần lượt là R và r.
Thể tích của khối nón cụt là:
1
V = π.h.( R 2 + Rr + r 2 )
3

r

 Khi r = 0 khối nón cụt trở
thành ……………. có thể tích:

h

R

1
2
V = π .h.R
3


 Khi r = R khối nón cụt trở thành ……………. có thể
tích:
2

V = π .h.R


CỦNG CỐ
b?

=∫f
S = ∫ ? ( x) .dx
a?

Em hãy nêu cơng thức để tính diện tích các hình vẽ sẵn ?
?
b

V
V = π ∫ ?f 2 ( x).dx
?
a

Em hãy nêu cơng thức để tính thể tích các khối theo hình vẽ ?


CỦNG CỐ
Em hãy nêu
cơng thức để
tính thể tích
của khối trịn
xoay tạo thành
khi cho đường
cong x = f(y)
quay xung
quanh trục Oy
như hình vẽ ?
2?

V= π ∫?2 ( y ).dy
V =π f

∫

?

−1