Bài giảng BT tính diện tích hình phẳng

TÝnh diªn tÝch, thÓ tÝch h×nh ph¼ng
Bµi 1: Tính diện tích của hình phẳng giới hạn bởi các đường: và
Cho là miềm kín giới hạn bởi các đường:
Tính diện tích của miền .
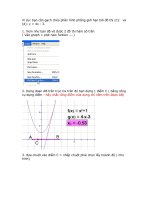
Bµi 2: Cho hàm số (C)
Tính diện tích hình phẳng giới hạn bởi (C) và đường thẳng
Bµi 3: Cho là miềm kín giới hạn bởi các đường :
Tính thể tích vật thể tròn xoay được tạo thành khi ta quay quanh trục Oy.
Bµi 4: Tính diện tích hình phẳng giới hạn bởi các đường:
và .
Bµi 5: Trong mặt phẳng với hệ tọa độ trực chuẩn Oxy,cho hình (D) giới hạn bởi các đường
.
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (D) quanh trục Ox.
Bµi 6: Tính diện tích hình phẳng giới hạn bởi các đường và trong mặt phẳng tọa
độ Oxy.
Bµi 7: Tính thể tích khối tròn xoay được tạo thành do quay quanh trục Ox hình phẳng hữu hạn giới hạn bở
các parabol:
và .
Bµi 8: Cho hàm số
Tính diện tích phần mặt phẳng hữu hạn được giới hạn bởi đồ thị (C) và tiếp tuyến của nó tại điểm thuộc đồ
thị có hoành độ bằng 2.
Bµi 9: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
và
Bµi 10: Tính diện tích S của hình phẳng được giới hạn bởi hai đường :
Đường parabol và đường thẳng
Bµi 11: Tính diện tích hình phẳng giới hạn bởi các đường : .
Bµi 12: Tính diện tích của hình phẳng giới hạn bởi parabol (P) có phương trình và hai tiếp
tuyến của (P) kẻ tại hai điểm A(1; 2) và B(4; 5).
Bµi 13: Tính diện tích hình phẳng giới hạn bởi:
Bµi 14: Gọi (D) là miền được giới hạn bởi các đường và (D) nằm
ngoài parabol .Tính thể tích vật tròn xoay được tao nên khi (D) quay xung quanh trục Ox.

Bµi 15: Tính diện tích hình giới hạn bởi các đường và
Bµi 16: Tính diện tích hình phẳng giới hạn bởi các đường cong
Bµi 17: Vẽ và tính diện tích hình phẳng giới hạn bởi các đường cong : và
GV: Mai ThÞ THUý