Tiet 28 Tinh chat cua hai tiep tuyen cat nhau

<span class='text_page_counter'>(1)</span>PHÒNG GIÁO DỤC VÀ ĐÀO TẠO BA VÌ TRƯỜNG THCS BA TRẠI. CHÀO MỪNG CÁC THẦY CÔ VỀ DỰ VỚI LỚP HỌC tiÕt 28 - Bµi 6. tÝnh chÊt cña hai tiÕp tuyÕn c¾t nhau. Gi¸o viªn : §inh Tiªn Hoµng.

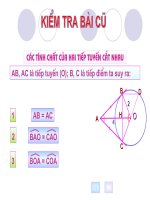
<span class='text_page_counter'>(2)</span> KIỂM TRA BÀI CŨ: - Phát biểu định lí về dấu hiệu nhận biết tiếp tuyến của đường tròn. Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn - Bài tập: Cho hình vẽ trong đó AB, AC theo thứ tự là các tiếp tuyến tại B, tại C của đường tròn (O). Hãy kể tên một vài đoạn thẳng bằng nhau, một vài góc bằng nhau. Lời giải: Xét  ABO và  ACO có : (tính chất tiếp tuyến) OB = OC (cùng là bán kính (O) AO chung   ABO =  ACO (cạnh huyền - cạnh góc vuông)  AB = AC ;.

<span class='text_page_counter'>(3)</span> Tiết 28 - Bài 6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU 1. Định lí về hai tiếp tuyến cắt nhau Định lí:. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì : • Điểm đó cách đều hai tiếp điểm. • Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. • Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm..

<span class='text_page_counter'>(4)</span> B. C. D A Thước phân giác.

<span class='text_page_counter'>(5)</span> B. D Tâm miếng gỗ hình tròn. A. C. ?2 Hãy nêu cách tìm tâm của một miếng gỗ hình tròn bằng “thước phân giác” Trả lời : Đặt miếng gỗ hình tròn tiếp xúc với hai cạnh của thước. - Kẻ theo “tia phân giác của thước, ta vẽ được một đường kính của hình tròn” - Xoay miếng gỗ rồi làm tiếp tục như trên, ta vẽ được đường kính thư hai. - Giao điểm của hai đường kính là tâm của miếng gỗ hình tròn.

<span class='text_page_counter'>(6)</span> Tiết 28 - Bài 6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU 1. Định lí về hai tiếp tuyến cắt nhau 2. Đường tròn nội tiếp tam giác ?3 Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác ; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h 80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn Chứng minh : Vì I thuộc tia phân giác góc A nên IE = IF Vì I thuộc tia phân giác góc B nên IF = ID Vậy IE = IF = ID  D, E, F cùng nằm trên một đường tròn (I ; ID)  Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.  Tâm đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác..

<span class='text_page_counter'>(7)</span> Tiết 28 - Bài 6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU 1. Định lí về hai tiếp tuyến cắt nhau 2. Đường tròn nội tiếp tam giác 3. Đường tròn bàng tiếp tam giác ?4 Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB (h 81). Chứng minh rằng ba điểm D, E, F nằm cùng trên một đường tròn có tâm K. Chứng minh : Vì I thuộc tia phân giác góc CBx nên KF = KD Vì I thuộc tia phân giác góc BCy nên KD = KE Vậy KE = KF = KD  D, E, F cùng nằm trên một đường tròn (I ; KD)  Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.  Tâm đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C ; hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B (hoặc C). Với một tam giác có ba đường tròn bàng.

<span class='text_page_counter'>(8)</span> K1. M A. K2 H B. D. C E. F. x. K. y.

<span class='text_page_counter'>(9)</span> HOẠT ĐỘNG NHÓM Bài tập : Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng. 1. Đường tròn nội tiếp tam giác 2. Đường tròn bàng tiếp tam giác. 3. Đường tròn ngoại tiếp tam giác. 4. Tâm của đường tròn nội tiếp tam giác. 5. Tâm của đường tròn bàng tiếp tam giác. a. là đường tròn đi qua ba đỉnh của tam giác. b. là đường tròn tiếp xúc với ba cạnh của tam giác. c. là giao điểm ba đường phân giác trong của tam giác. d. là đường tiếp xúc với một cạnh của tam giác và phần kép dài của hai cạnh kia. e. là giao điểm của hai đường phân giác ngoài của tam giác.. 1-b 2-d 3-a. 4-c. 5-e.

<span class='text_page_counter'>(10)</span> Bài tập 26 a : (tr 115 SGK) Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). a) Chứng minh rằng OA vuông góc với BC.. Chứng minh : Có AB = AC (tính chất tiếp tuyến)   ABC cân tại A. Mà AO là đường phân giác của góc BAC nên cũng là đường trung trực của BC nên AO  BC.

<span class='text_page_counter'>(11)</span> Tiết 28 - Bài 6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU 1. Định lí về hai tiếp tuyến cắt nhau Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì : •. Điểm đó cách đều hai tiếp điểm.. •. Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.. •. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.. 2. Đường tròn nội tiếp tam giác  Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.  Tâm đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác.. 3. Đường tròn bàng tiếp tam giác  Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.  Tâm đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C ; hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B (hoặc C). Với một tam giác có ba đường tròn bàng tiếp..

<span class='text_page_counter'>(12)</span> HƯỚNG DẪN VỀ NHÀ - Học thuộc định lí về tính chất của hai tiếp tuyến cắt nhau - Nắm vững các khái niệm về đường tròn nội tiếp tam giác; tam giác ngoại tiếp đường tròn; đường tròn bàng tiếp tam giác. - Bài tập : 26 (b,c), 27, 28 tr 115, 116 SGK Hướng dẫn bài tập 26 b, c b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO c) Tính độ dài các cạnh của tam giác ABC ; biết OB = 2cm, OA = 4cm..

<span class='text_page_counter'>(13)</span> KÍNH CHÚC CÁC THẦY CÔ GIÁO SỨC KHOẺ, HẠNH PHÚC CHÚC CÁC EM HỌC SINH CHĂM NGOAN, HỌC GIỎI.

<span class='text_page_counter'>(14)</span>