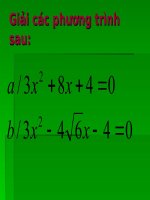Chuong IV 5 Cong thuc nghiem thu gon

<span class='text_page_counter'>(1)</span>•. NHIỆT LIỆT CHÀO MỪNG QUÝ THẦY CÔ VỀ DỰ GIỜ LỚP 9A. LỚP 9A CHĂM NGOAN, HỌC GIỎI.

<span class='text_page_counter'>(2)</span> KIỂM TRA BÀI CŨ. • Hãy nêu công thức nghiệm của phương trình bậc hai ?.

<span class='text_page_counter'>(3)</span> Phương trình ax2 + bx + c = 0 (a  0). Công thức nghiệm của phương trình bậc 2 ∆ = b2 – 4ac. + Nếu ∆ > 0: Phương trình có hai nghiệm phân biệt. b  x1 = 2a b  x2= 2a. + Nếu ∆ = 0: Phương trình có nghiệm kép:. b x1 = x 2  2a. + Nếu ∆ < 0: Phương trình vô nghiệm..

<span class='text_page_counter'>(4)</span> 2 Đối với phương trình ax  bx  c 0 ( a 0 ) trong trường hợp hệ số b có thể biểu diễn được dưới dạng b = 2b’. [ VD : b  6 ; b 4 3 ; b 2( m  2) ]. ta còn có công thức nghiệm ngắn gọn hơn, giải phương trình đơn giản hơn, đó là:. CÔNG THỨC NGHIỆM THU GỌN.

<span class='text_page_counter'>(5)</span> ?1. Từ bảng kết luận của bài trước hãy dùng các đẳng thức b = 2b’ và ?1  = 4’ để suy ra những kết luận sau:. Đối với phương trình: ax2 + bx + c =0 (a0) và b = 2b’, ’ = b’2 - ac * Nếu ’ > 0 thì phương trình có hai nghiệm phân biệt:.  b'  Δ' x1 a. b'  Δ' x 2 a. * Nếu ’ = 0 thì phương trình có nghiệm kép:. * Nếu ’ < 0 thì phương trình vô nghiệm..  b' x1 x2  a.

<span class='text_page_counter'>(6)</span> * Công thức nghiệm thu gọn: Đối với phương trình ax2 + bx +c = 0 (a ≠ 0) và b = 2b’, ’ = b’2 - ac: • Nếu ’ > 0 thì phương trình có 2 nghiệm phân biệt:.  b '  ' x1  a  b ' ' x2  a. Trong thực hành khi nào ta nên dùng công thức nghiệm thu gọn để giải phương trình bậc hai?. • Nếu ’ = 0 thì phương trình có nghiệm kép :. b' x1 x2  a • Nếu ’ < 0 thì phương trình vô nghiệm..

<span class='text_page_counter'>(7)</span> *Lưu ý: Nếu hệ số b là số chẵn, hay là bội chẵn của một căn, một biểu thức, chẳng hạn: b = 4, b = -6 2 , b = 2(m-1),… thì ta nên dùng công thức nghiệm thu gọn để giải phương trình bậc hai..

<span class='text_page_counter'>(8)</span> Các bước giải phương trình bậc hai bằng công thức nghiệm thu gọn:. Để giải phương trình bậc hai bằng công thức Bước 1: Xác địnhthu cácgọn hệ sốta a,cần b’, c. nghiệm thực hiện những bước nào? ’ = b’2 - ac rồi so sánh kết quả với 0. Bước 2: Tính. Bước 3: Kết luận số nghiệm của phương trình. Bước 4: Tính nghiệm theo công thức nếu phương trình có nghiệm..

<span class='text_page_counter'>(9)</span> ?2 Giải phương trình 5x2 + 4x – 1 = 0 bằng cách điền vào những chỗ trống: 5 2 a = ... ; b’ = .... ; c =-1 .... 3  ' = 2....2 –5.(-1) = 9 ;  ' = ..... Nghiệm của phương trình: -2+3 1 x1 = .... = …… 5 5. -2-3 ; x 2 = ..... = ..... -1 5.

<span class='text_page_counter'>(10)</span> ?3 Xác định a, b’, c rồi dựng công thức nghiệm thu gọn giải các phương trình: 2. a )3x  8 x  4 0. 2. b ) 7 x  6 2 x  2  0.

<span class='text_page_counter'>(11)</span>

<span class='text_page_counter'>(12)</span>

<span class='text_page_counter'>(13)</span> HƯỚNG DẪN VỀ NHÀ - Học thuộc công thức nghiệm thu gọn. - Xem lại các ví dụ đã làm - Làm bài tập 17, 18, 19, 20, 21, 24(SGK-T49).

<span class='text_page_counter'>(14)</span>