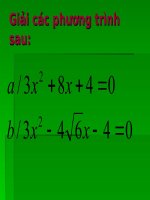Chuong IV 5 Cong thuc nghiem thu gon

Tuần 29

Ngày soạn: 18/ 03/ 2018

Tiết 57

Ngày dạy: 20/ 03/ 2018
LUYỆN TẬP

I. MỤC TIÊU: Qua bài này HS cần:
1. Kiến thức:
- Củng cố lại cho học sinh cách giải phương trình bậc hai một ẩn bằng cơng
thức nghiệm
2. Kĩ năng: Rèn kỹ năng giải phương trình bậc hai bằng cơng thức thức
nghiệm.
3. Thái độ:
- Học sinh tích cực, chủ động trong học tập
- Các em làm bài kiểm tra 15 phút thật nghiêm túc, đạt kết quả tốt
II. CHUẨN BỊ
1. Giáo viên: Thước, phấn, giáo án
2. Học sinh: Học bài cũ, đọc trước bài mới, ĐDHT
III. PHƯƠNG PHÁP: Suy luận, vận dụng, vấn đáp
IV. TIẾN TRÌNH LÊN LỚP
1. Tổ chức (1 phút) KTSS
2. Kiểm tra bài cũ: Không kiểm tra
3. Bài mới (25 phút)
Hoạt động của GV và HS

Nội dung

Bài tập 16 (SGK/45) (12 phút)

- GV ra bài tập, sau đó u cầu HS Dùng cơng thức nghiệm của phương trình
làm bài 16 dùng cơng thức nghiệm để bậc hai để giải phương trình:
giải phương trình bậc hai 1 ẩn.
c) 6x2 + x - 5 = 0
a=6;b=1;c=-5
- Hãy xác định các hệ số a; b; c để
 = b2 - 4ac = 12 - 4. 6.(- 5)
giải phương trình phần c).
= 1 + 120 = 121 > 0
- Để tính được nghiệm của phương    121 11
Phương trình có hai nghiệm phân biệt:
trình trước hết ta phải tính gì ?
( Tính ) Nêu cách tính  ?
- GV u cầu 1 học sinh lên bảng tính
 sau đó nhận xét  và tính nghiệm


 1  121  1  11 10 5

 
 x1 

2.6
12
12 6

 x   1  121   1  11  1
 2
2.6
12

của phương trình trên.

Vậy phương trình có 2 nghiệm phân biệt:
5
x1= 6 ; x2 = -1

- Tương tự hai học sinh lên bảng giải
tiếp, em hãy giải tiếp các phần còn lại d) 3x2 + 5x + 2 = 0 (a = 3 ; b = 5 ; c = 2 )
của bài tập trên.
Ta có  = b2 - 4ac = 52 - 4.3.2
= 25 - 24 = 1
- Dựa vào đâu mà ta có thể nhận xét
   1 1
về số nghiệm của phương trình bậc Do  = 1 > 0
 Phương trình có hai nghiệm phân biệt:
hai một ẩn ?

 5  1  5 1  4  2

 
 x1 

2.3
6
6
3

 x   5  1   5  1  1

 2
2.3
6

+) Qua bài tập trên GV lưu ý cho học
sinh cách vận dụng cơng thức nghiệm
vào giải phương trình bậc hai 1 ẩn;
cách trình bày lời giải và lưu ý khi Vậy phương trình có 2 nghiệm phân biệt:
tính toán.
2
x1 = 3 ; x2 = -1
e) y2 - 8y + 16 = 0(a = 1; b = - 8; c = 16)
Ta có:  = b2 - 4ac =(-8)2 - 4.1.16
= 64 - 64 = 0
Do  = 0  phương trình có nghiệm kép:
x1 x2 

 ( 8)
4
2.1

Vậy phương trình có nghiệm kép:
x1 = x2 = 4
Bài tập 21 (SBT/41) (13 phút)
- GV cho học sinh làm bài 21 Giải phương trình:
(SBT/41)
2
a) 2 x  2 2 x  1 0
- Hướng dẫn:
a = 2 ; b  2 2 ; c = 1

Hãy tính  sau đó nhận xét  và suy
2
ra nghiệm của phương trình
 2 2   4.2.1 8  8 0

2
 = b - 4ac =
- Gọi 2 học sinh lên bảng làm bài.
Phương trình có nghiệm kép:
2
Gợi ý: viết  =



1 4 2 8  1 2 2



x1  x2 

 ( 2 2)
2

2.2
2

- Học sinh lên bảng tính nghiệm của
1  2 2  x  2 0
phương trình.
b) 2x2 - 

a = 2 ; b = - ( 1  2 2) ; c = - 2






2



  1  2 2   4.2.  2

 = b2 - 4ac = 



1  4 2  8  8 2

=



  1 2 2



1 4 2  8  1 2 2



2



2

>0

1  2 2

Phương trình có hai nghiệm phân biệt:
1  2 2 1  2 2 1
x1 

2.2
2
1 2 2  1 2 2
x2 
 2
2.2

4. Củng cố: (17 phút) Cho HS làm bài kiểm tra 15 phút
A. Đề
Câu 1(4,5 điểm) Xác định hệ số a, b, c của các phương trình sau:
a) 2x2 + 3x + 2 = 0
b) x2 - 4 x = 0
c) x2 - 4 = 0
Câu 2 (5,5 điểm) Giải phương trình sau: x2 - 3x - 4 = 0
B. Biểu điểm và đáp án

Câu

Nội dung

Điểm

Câu 1 a) 2x2 + 3x + 2 = 0
a = 5, b = -1, c = 2

1.5

b) x2 - 4 x = 0
a = 1, b = -4, c = 0

1.5

c) x2 - 4 = 0
a = 1, b = 0, c = -4

1.5

Câu 2 x2 - 3 x - 4 = 0
a = 1, b = -3, c = -4

1.0

 = b2 - 4ac = 9 – 4.1.(-4) = 25 > 0

1.0



  25 5

Phương trình có hai nghiệm phân biệt:

1.0
0.5
1.0
1.0


35

 x1  2 4

 x  3  5  1
 2
2

5. Hướng dẫn về nhà (1 phút)
- Học thuộc cơng thức nghiệm của phương trình bậc hai một ẩn.
- Giải tiếp các phần còn lại của các bài tập trên
- Đọc trước “ Công thức nghiệm thu gọn”
*. RÚT KINH NGHIỆM
..........................................................................................................................
...........................................................................................................................
..........................................................................................................................
...........................................................................................................................
..........................................................................................................................

Tuần 29

Ngày soạn: 18/ 03/ 2018

Tiết 58

Ngày dạy: 21/ 03/ 2018
Bài 5: CÔNG THỨC NGHIỆM THU GỌN

I. MỤC TIÊU: Qua bài này HS cần:
1. Kiến thức:
- Giúp học sinh hiểu được cơng thức nghiệm thu gọn và cách giải phương
trình bậc hai theo công thức nghiệm thu gọn
- Củng cố cách giải phương trình bậc hai theo cơng thức nghiệm.
2. Kĩ năng: Rèn kỹ năng giải phương trình bậc hai theo công thức nghiệm
và công thức nghiệm thu gọn.
3. Thái độ: Tích cực, chủ động, nghiêm túc.
II. CHUẨN BỊ
1. Giáo viên: Thước, phấn, phiếu học tập, bảng phụ, bút lông
2. Học sinh: Học bài cũ, đọc trước bài mới, ĐDHT
3. Phương pháp: Suy luận, vận dụng, vấn đáp
III. TIẾN TRÌNH LÊN LỚP
1. Tổ chức: (1 phút) KTSS
2. Kiểm tra bài cũ: (5 phút)
Gv: Nhắc lại công thức nghiệm của phương trình bậc hai
Gọi 2 HS lên bảng làm bài tập
Giải các phương trình sau:
a) 2x2 + 3x - 1 = 0

b) x2 + 2x – 3 = 0
3. Bài mới (36 phút)
Đối với phương trình ax2 + bx + c = 0 ( a  0 ), trong nhiều trường hợp nếu
đặt b = 2.b’ thì việc tính tốn để giải phương trình sẽ đơn giản hơn. Cụ thể ta cùng
tìm hiểu trong bài học hơm nay.
Hoạt động của GV và HS

Nội dung

1. Công thức nghiệm thu gọn (17 phút)
Xét p. trình ax2 + bx + c = 0 ( a  0 ) Xét p. trình ax2 + bx + c = 0 ( a  0 )
đặt b = 2b’
- Hãy tính  theo b’ ?
HS:
GV: Đặt ’ = b’2 – ac, ta có  = 4’

Khi b = 2b’  ta có:  = b2 - 4ac
  = (2b’)2 - 4ac = 4b’2 - 4ac

= 4 (b’2 - ac)
Kí hiệu: ’ = b’2 - ac   = 4’


GV yêu cầu HS thực hiện ?1 ( sgk) ?1 (Sgk - 48)
biến đổi từ công thức nghiệm ra công + ’ > 0   > 0
thức nghiệm thu gọn.
 Phương trình có hai nghiệm phân biệt:
x1 

 b    2b ' 4 '  b '  '



2a
2a
a
;

x2 

 b    b '  '

2a
a

+ ’ = 0   = 0
Phương



x1 x2 

trình

có

nghiệm

kép:

 b  2b '  b '



2a
2a
a

+ ’ < 0   < 0
- GV gọi HS nêu lại công thức nghiệm
thu gọn



Phương trình vơ nghiệm.

2. Áp dụng (16 phút)
- GV yêu cầu học sinh thực hiện ? 2
( sgk ) (bảng phụ)

? 2 Giải phương trình 5x2 + 4x - 1 = 0

bằng cách điền vào những chỗ trống

- HS xác định các hệ số của phương a = 5 ; b’ = 2 ; c = - 1
trình
’ = 22 - 5. ( -1) = 4 + 5 = 9 > 0
- Nêu cơng thức tính ’ và tính ’
 '  9 3

của phương trình trên
Nghiệm của phương trình:

- So sánh ’ với 0 và suy ra số
 23 1
 2 3
nghiệm của phương trình trên ?
x1 
 ; x2 
 1
5

GV: Gọi HS lần lượt lên bảng điền
vào chỗ trống.

5

5

?3 ( sgk )
Hãy thực hiện ?3 tương tự như cách
làm ở ?2
a) 3x2 + 8x + 4 = 0
- GV chia lớp thành các nhóm cho a = 3; b’ = 4; c = 4
học sinh giải mỗi nhóm 1 câu trên
' = b'2 - ac = 42 - 3.4 = 16 - 12 = 4 > 0
phiếu học tập rồi so sánh kết quả.


- Các nhóm làm ra phiếu học tập
- GV thu phiếu học tập và nhận xét

 '  4 2

Phương trình có hai nghiệm phân biệt là:
x1 

 42
2
 4 2

; x2 
 2
3
3
3

- GV nhận xét và chốt lại cách giải b) 4x2 – 12x + 9 = 0
phương trình bằng công thức nghiệm a = 4; b’ = -6; c = 9


’= b’2 - ac = (-6)2 – 4.9 = 0
Phương trình đã cho có nghiệm kép là:
 b '  (  6) 3

2
x1 = x2 = a = 4

4. Củng cố: (3 phút)
Xác định hệ số a, b’, c trong các pt sau:
a. -3x2 - 8x + 4 = 0 ; 5x2 + 4x + 1 = 0 ; 7x2 - 2x + 2 = 0
5. Hướng dẫn về nhà: (1 phút)
- Học thuộc và nắm chắc công thức nghiệm và cơng thức nghiệm thu gọn để

giải phương trình bậc hai một ẩn có hệ số b chẵn.
- Xem lại các ví dụ và bài tập đã chữa.
- Giải bài tập 17; 18; 20 (Sgk/49)
*. RÚT KINH NGHIỆM
............................................................................................................................
............................................................................................................................
............................................................................................................................
............................................................................................................................
............................................................................................................................


Bài tập 24 (SBT/41) (9 phút)
- GV yêu cầu học sinh đọc đề bài 24 Tìm m để phương trình có nghiệm kép:
(SBT /41)
a) mx2 - 2(m - 1)x + 2 = 0
+) Hãy nêu cách giải bài bài tập
(a = m; b = - 2(m - 1); c = 2)
này ?
Để phương trình có nghiệm kép
- Phương trình bậc hai có nghiệm kép
 m 0
khi nào ? Một phương trình là bậc
 a 0

2

hai khi nào ?
  0    2(m  1)   4.m.2 0
- Vậy với những điều kiện nào thì
một phương trình có nghịêm kép ?

 m 0
 2
 4m  16m  4 0

- HS : Để phương trình có nghiệm
Để  = 0  4m2 - 16m + 4 = 0
kép:
 m2 - 4m + 1 = 0
 a 0

  0

- Từ đó ta phải tìm những điều kiện
gì?
+ Gợi ý: xét a  0 và  = 0 từ đó tìm
m

Có m = ( - 4)2 - 4.1.1 = 12

42 3
2  3
 m1 

2

 m  4  2 3 2  3
2
2
 

- Học sinh làm sau đó GV chữa bài Vậy với m1 2  3 hoặc m2 2  3 thì
lên bảng chốt cách làm.
phương trình đã cho có nghiệm kép