ma tran hk1 chi tiet

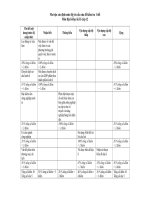
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I MƠN TỐN LỚP 12 NĂM HỌC 2018 – 2019

CHỦ ĐỀ
Ứng dụng đạo
hàm để khảo
sát sự biến
thiên và vẽ đồ
thị hàm số
Hàm số mũ,
hàm
logarit,hàm số
lũy thừa

NB
30 %
TH
TNKQ
TL
TNKQ
3
1
5

0.75

1.0

4

1.25

1.0

0.0

10
TỔNG

ST
T

Mức độ

1

Nhận biết

2
3
4
5
6
7
8
9

Nhận biết
Nhận biết
Thông hiểu
Thông hiểu
Thông hiểu

Thông hiểu
Thông hiểu
Vận dụng

10
11
12
13

Vận dụng
Nhận biết
Nhận biết
Nhận biết

14
15
16
17

Nhận biết
Thông hiểu
Thông hiểu
Vận dụng

18

Vận dụng

19

Vận dụng

20 %
TL

0.5

0.0

3

0.5

0.0

VDC
TNKQ

20 %
TL

0.0
0

0.75

0.0

1

0.0

1.0

0.0

9

1.0

0.0

1
2.5
3.5

9
1.0

0.0

0.0
1

2.25
3.25

1

5

1.0

1
1.25
2.25

0.0
0

0.5

1.0

0.0
1

0.0
1.0

1.0
1

3
1.0

1.0

2.25

0.0

1
0.5

2.5

2

2
0.25

TỔNG
TNKQ
TL
10
1

0.0

1
0.5

Khối cầu, khối 1
trụ, khối nón

VD
TNKQ
2

0.0

2

Thể tích khối 2
đa diện

30 %
TL

1.0
1

0.75
24

1.0

MƠ TẢ NỘI DUNG CHI TIẾT
Nội dung kiểm tra
TRẮC NGHIỆM
Cho hàm số có bảng xét dấu đạo hàm. Tìm khoảng đồng biến
hoặc nghịch biến.
Số cực trị của hàm số bậc 3 hoặc trùng phương
Tiệm cận đứng và tiệm cận ngang của hàm nhất biến
Tìm giá trị cực đại hoặc cực tiểu của hàm đa thức
Tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số trên đoạn
Dạng đồ thị hàm số bậc ba
Dạng đồ thị hàm số trùng phương
Viết phương trình tiếp tuyến với đồ thị hàm số tại một điểm
Tìm m để hàm số đồng biến hoặc nghịch biến trên một

khoảng
Bài toán thực tế có liên quan đến tìm GTLN, GTNN
Cơng thức lũy thừa
Cơng thức logarit hoặc bài tốn có chứa logarit bấm máy được
x
Đạo hàm của hàm số y a hoặc y log a x
Viết một số dưới dạng lũy thừa với số mũ hữu tỉ
Tìm x thỏa mãn phương trình mũ hoặc logarit cơ bản
Tìm tập xác định của hàm số logarit
Tìm số giá trị x thỏa mãn phương trình mũ hoặc logarit giải
bằng phương pháp thường gặp
Tính giá trị biểu thức chứa logarit có quy luật, khơng bấm
máy tính được.
Bài tốn thực tế có liên quan đến lãi kép hoặc cơng thức tăng
trưởng mũ.

1.0
4

6.0
10.0

4.0


20

Thơng hiểu

21

Thơng hiểu

22
23
24

Nhận biết
Nhận biết
Thơng hiểu

1
2

Nhận biết
Thơng hiểu

3

Vận dụng

4

Vận dụng
cao

Tính thể tích của khối chóp có hai mặt bên vng góc với mặt
đáy, biết chiều cao và tính diện tích đáy.
Tính thể tích của khối lăng trụ tam giác đều có cho cạnh bên
và cạnh đáy

Cơng thức thể tích khối trụ.
Cơng thức diện tích xung quanh của hình nón.
Tính thể tích khối cầu ngoại tiếp hình chóp.
TỰ LUẬN
Tìm khoảng đồng biến, nghịch biến của hàm số đa thức
Tính thể tích khối chóp có cạnh bên vng góc với mặt đáy,
hoặc lăng trụ đứng, có cho giả thiết góc giữa đường thẳng và
mặt phẳng để tính chiều cao của đa diện đó.
Bài tốn cực trị về thể tích hoặc diện tích của khối cầu hoặc
khối nón hoặc khối trụ
Sử dụng tính đơn điệu của hàm số để chứng minh bất đẳng
thức có chứa hàm số mũ, hàm số logarit.