Bài giảng động cơ học máy
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.75 MB, 106 trang )
1
ĐỘNG LỰC HỌC MÁY
HÀ NỘI - 2006
1
ĐỘNG LỰC HỌC CÁC HỆ DẪN ĐỘNG
HỆ THỐNG CỨNG
1. Phƣơng trình chuyển động của hệ thống cứng
;,,
2
)(
2
dxtvxP
vxm
d
.,,
2
1
2
2
2
tvxP
dt
dx
dx
xmd
dt
xd
xm
Trƣờng hợp: m(x)=m=C
te
;P(x,v,t)=P = C
te
.
2
2
P
dt
xd
m
;,,
2
2
dtM
J
d
Chuyển động thẳng:
Chuyển động quay:
Trƣờng hợp: J(φ)=J=C
te
;M(φ,ω,t)=M=C
te
.
2
2
M
dt
d
J
.,,
2
1
2
2
2
tM
dt
d
J
d
d
dt
d
J
2
2.Lời giải tổng quát của phƣơng trình chuyển động của hệ
thống cứng
;,,
22
0
2
2
dxtvxPv
m
dt
dxxm
x
o
o
;
,,2
2
0
o
o
x
v
xm
m
xm
dxtvxP
dt
dx
m
o
,v
o
-khối lƣợng và vận tốc ban đầu
;
,,2
2
dtv
xm
m
xm
dxtvxP
x
t
o
t
o
o
x
o
3
2
2
2
,,2
o
o
x
o
v
xm
m
xm
dxtvxP
dt
d
dt
xd
a
;
,,2
0
2
000
x
x
xm
vm
xm
dxtvxP
dx
t
;
2
2
0
v
m
Px
dt
dx
Trƣờng hợp m(x)=m=C
te
;
P(x,v,t)=P=C
te
;
;
2
2
m
P
dt
xd
;
2
2
0
v
m
Px
dx
dt
.
2
0
2
0
vv
m
Px
P
m
t
.
0
vt
m
P
dt
dx
4
Trƣờng hợp: J(φ)=J=C
te
;M(φ,ω,t)=Mφ/φ
1
.
;
2
2
0
1
2
2
0
0
1
J
M
J
d
M
dt
d
;ln
0
1
1
0
2
0
1
2
A
J
M
M
J
J
M
d
t
.
2
0
1
2
J
M
A
.
2
1
1
2
0
1
2
0
J
M
t
J
M
t
e
M
J
e
5
Trƣờng hợp
.0;;
0
1
1
MMCJJ
te
;
1
1
2
2
M
dt
d
J
dt
d
J
;
1
1
d
M
J
dt
;ln
1
11
M
J
t
;1
1
1
J
tM
e
dt
d
;
1
2
2
J
tM
e
J
M
dt
d
.1
1
2
1
1
J
tM
e
M
J
t
6
Trƣờng hợp
.1;
1
t
t
MtMCJJ
te
;1
1
1
2
2
t
t
M
J
dt
d
;
2
1
1
J
t
t
M
dt
d
.
3
1
2
1
2
1
t
t
t
M
J
te
CMiJiJ ;J
2
1
2
2
00
2
0
Trƣờng hợp
;
2
2
00
2
1
iJ
M
dt
d
.
2
1
2
00
M
iJ
dt
7
PHƢƠNG PHÁP CHUNG GIẢI PHƢƠNG TRÌNH
CHUYỂN ĐỘNG CỦA HỆ ĐÀN HỒI
)1.2(;
.
2
2
2
1
1
1
tfya
dt
yd
a
dt
yd
a
dt
yd
n
n
n
n
n
n
n
a
1
,a
2
,…,a
n
– các hệ số không đổi đã biết;
f(t) – hàm thời gian đã biết.
Phƣơng trình đặc tính của phƣơng trình thuần nhất
tƣơng ứng:
0
2
2
1
1
n
nnn
axaxax
8
Các nghiệm x
1
,x
2
,…,x
n
có thể là:
1/ Nghiệm thực và riêng biệt; 2/ Nghiệm kép;
3/ Nghiệm ảo thuần tuý; 4/ Nghiệm phức liên hợp;
Nghiệm tƣơng ứng của phƣơng trình thuần nhất là:
; /1
2
2
1
10
t
n
x
n
txtx
eCeCeCy
; /2
12
3210
xtn
n
etCtCtCCy
;cossin cos
sincossin/3
21224
231211
txCtxCtxC
txCtxCtxCy
nnnn
teCteCteC
teCteCteCy
n
t
n
nn
t
n
n
t
ttt
cossin co s
sincossin/4
2122
2
4
2
2
31
1
21
1
10
Nghiệm tổng quát của phƣơng trình ( 2.1 ):
.*
0
yyy
9
CÁC TRƢỜNG HỢP CỤ THỂ
1. Phƣơng trình bậc hai với f(t) tuỳ ý.
;
2
2
tfby
dt
dy
a
dt
yd
xey
at
2
tFtfex
a
b
dt
xd
at
2
2
2
2
4
)8.2(
( 2.8 )
( 2.9 )
;0
4
/
2
1
2
k
a
ba
tFxk
dt
xd
2
1
2
2
( 2.10 )
;sincos
1211
tkCtkCx
o
tkttktx
11
sincos*
;0sincos
11
tk
dt
d
tk
dt
d
(2.11);
(2.12)
tFtk
dt
d
tk
dt
d
k
111
cossin
(2.13)
(2.14)
10
(2.13)+(2.14)
.cos
1
;sin
1
1
1
1
1
tktF
kdt
d
tktF
kdt
d
.sintFcos
1
costFsin
1
*
11
1
11
1
tdtktk
k
tdtktk
k
x
t
o
t
t
o
t
Thay t dƣới dấu tích phân bằng
*;xxx
.sinF
1
*
1
1
dtk
k
x
t
o
t
.sinF
1
sincos
1
1
1211
dtk
k
tkCtkCx
t
o
t
.sinF
1
sincos
1
1
1211
2
t
o
t
at
dtk
k
tkCtkCey
( 2.17 )
( 2.16 )
( 2.15 )
1
Chương 3
TẢI TRỌNG ĐỘNG LỰC HỌC
VÀ DAO ĐỘNG CỦA CÁC BỘ TRUYỀN ĐỘNG
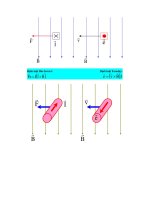
1.Trường hợp mở máy (hoặc hãm máy) không tải.
a. Hệ hai khối lượng có tần số cao.
te
CM
J
2
,φ
2
J
1
,φ
1
M
k
J
2
,φ
2
J
1
,φ
1
M
k
a/ b/
M – momen quy đổi của động cơ
khi mở máy (phanh hãm khi
dừng máy);
J
1
,J
2
– momen qt quy đỏi của khối
lượng dẫn và bị dẫn;
φ
1
,φ
2
- chuyển vị góc của các khối
lượng này;
k - độ cứng quy đổi.
*/ trường hợp mở máy (hoặc hãm khi momen hãm tác dụng lên
khâu dẫn:
;)(
21
2
1
2
1
Mk
dt
d
J
;0)(
21
2
2
2
2
k
dt
d
J
(1)
2
φ = φ
1
– φ
2
– chuyển vị góc tương đối của 2 khối lượng;
;
)(
cos1
)(
21
21
21
2
t
JJ
JJk
JJk
MJ
(2)
Mở máy: t = 0; φ = 0;
;0
dt
d
;
)(
121
21
2
2
J
M
JJ
JJk
dt
d
(3)
;
)(
2
21
2
max
JJk
MJ
;
2
21
2
maxmax
JJ
MJ
kM
(4) (5)
*/ Momen hãm tác dụng lên khâu bị dẫn:
;
2
21
1
max
JJ
MJ
M
(5a)
3
b. Hệ hai khối lượng có tần số thấp.
)
1
1(
1
0
0
dt
d
MM
M
0
– momen q/đổi trên trục đ/c khi bắt đầu chạy không;
ω
0
- vận tốc chạy không của trục đ/c;
)
1
1()(
1
0
021
2
1
2
1
dt
d
Mk
dt
d
J
0)(
21
2
2
2
2
k
dt
d
J
(6)
(7)
Đặt φ = φ
1
– φ
2
- biến dạng của khâu đàn hồi;
0
)(
J
21
2
2
21
21
3
3
1
0
4
4
dt
d
JJ
kM
dt
d
JJ
kJJ
dt
d
M
dt
d
o
o
o
Phương trình đặc tính:
0
)(
J
21
2
21
21
3
1
0
4
x
JJ
kM
x
JJ
kJJ
x
M
x
o
o
o
(8)
(9)
4
Nghiệm:
;
2
1
J3
3
32
3
32
1
abbabb
M
z
o
o
;2
10
J
M
zx
o
;;
21
iuzxiuzx
;cossin tDetCeBeA
ztztxt
Với hệ thực
0
3
2
ab
(12)
;
2
3
3
32
3
32
abbabbu
;
9
3
)(
2
1
2
0
2
21
21
J
M
JJ
JJk
a
o
;
2
)2(
9
3
21
21
2
1
2
0
10
JJ
kJJ
J
M
J
M
b
o
o
(13)
(14)
(10)
(11)
(15) Nghiệm của (8):
Với máy thật x<0; z<0, khi t các thành phần (15) trừ A
;0
o
x
;00;
21
At
;00;0 DB
dt
d
t
5
Tìm được:
;
])[(
)(
22
1
0
uxzuJ
xzM
C
;
])[(
22
1
0
uxzJ
M
DB
;cossin(
])[(
22
1
0
21
tt
u
xz
ee
uxzJ
kM
kM
mm
ztxt
;)(
1
])[(
22
22
1
0
max
21
uxz
u
ee
uxzJ
kM
kM
mm
ztxt
;
1
u
zx
arctg
u
t
m
(16)
(17)
(18)
6
2. Trường hợp mở máy (hoặc hãm) có tải.
a. Hệ hai khối lượng có tần số cao.
)(
te
CM
11
,
J
22
,
J
k
M
M
c
;)(
21
2
1
2
1
Mk
dt
d
J
;)(
21
2
2
2
2 c
Mk
dt
d
J
(19)
M
c
: hàm của vị trí, vận tốc, thời gian hoặc hằng số.
Trường hợp φ=φ
1
-φ
2
- biến dạng khâu đàn hồi.
;0;;0
2
dt
d
k
M
t
c
;
)(
)(
)(
cos
)(
sin
21
2
21
21
21
21
k
M
JJk
JMM
t
JJ
JJk
Bt
JJ
JJk
A
cc
(20)
Trong một số trường hợp có thể coi trong pha đầu chỉ có khối
lượng J
1
ch, đg cho tới khi φ=M
c
/k có thể coi thời điểm đó
là gốc thời gian
nghĩa là từ thời điểm đó cả 2 khối lượg mới cùng chuyển động.
7
;
)(
)(
;0
21
2
JJk
JMM
BA
c
;
)(
cos1
)(
)(
21
21
21
2
k
M
t
JJ
JJk
JJk
JMM
cc
;
)(
cos1
)(
21
21
21
2
3 c
c
Mt
JJ
JJk
JJ
JMM
kM
;
)(2
21
2
3
max
c
c
M
JJ
MMJ
M
Trg hợp hãm máy với momen hãm đặt lên khối lượng 1:
;
)(2
21
2
3
max
c
c
M
JJ
MMJ
M
Hãm máy với momen hãm đặt trên khối lượng 2:
;
)(2
21
2
3
max
c
c
M
JJ
MMJ
M
8
Trường hợp động cơ phát hành không biến trở.
- Giai đoạn 1.
Khối lượng 1 quay, khối lượng 2 đứng im cho tới
khi momen trong khâu đàn hồi bằng M
c
:
);(;
1
1
ttMk
c
;
J
cos
J
sin
1
1
1
1
1
k
M
t
k
Bt
k
A
;0;0;0
1
1
dt
d
t
(19a)
);
J
cos1(
1
1
t
k
k
M
(27)
;
J
sin
J
11
1
t
kk
k
M
dt
d
(28)
(29)
Kết thúc giai đoạn 1: t = t
1
;arccos;)
J
cos1(
1
11
1
M
MM
c
J
tMt
k
M
c
c
(31)
;
)2(
1
1
1
kJ
MMM
dt
d
cc
tt
(32)
9
- Giai đoạn 2. Cả hai khối lượng cùng chuyển động.
Ph trình chuyển động: (19) và (20)
Điều kiện ban đầu:
1
1
;;0
tt
c
dt
d
dt
d
k
M
t
;
)2(
1
21
2
JJ
JMMM
k
A
cc
;
)(
)(
21
2
JJk
JMM
B
c
t
JJ
JJk
JJ
JMMM
kM
cc
21
21
21
2
)(
sin
)2(
c
cc
M
JJ
JMM
t
JJ
JJk
JJ
JMM
)(
)(
)(
cos
)(
21
2
21
21
21
2
(33a)
;
)()(
)2(
21
2
21
2
2
21
2
max c
cc
cc
M
JJ
JMM
JJ
JMM
MMM
JJ
J
M
(34)
10
b. Hệ hai khối lượng tần số thấp.
)
1
1((
1
dt
d
MM
o
n
);
1
1()(
1
21
2
1
2
1
dt
d
Mk
dt
d
J
o
n
;)(
21
2
2
2
2 c
Mk
dt
d
J
(35)
Lời giải của (35) là (15).
*/ Trường hợp có biến trở.
;0;)(;0
21
dt
d
k
M
t
c
;
])[(
;
22
1
uxzJ
MM
B
k
M
A
cnc
])[(
)(
;
])[(
))((
22
1
22
1
uxzJ
MM
D
uxzuJ
xzMM
C
cncn
;cossin
])[(
)(
22
1
3 c
ztxt
cn
Mutut
u
xz
ee
uxzJ
cMM
kM
;
)(
])[(
)(
22
22
1
3
max
c
ztxt
cn
M
u
uxz
ee
uxzJ
kMM
M
mm
u
zx
arctg
u
t
m
1
11
*/ Trường hợp không có biến trở bậc trước phát hành: 2 giai đoạn.
GĐ 1: Khối lượng chủ động bắt đầu ch/đg đều khi momen trong
khâu đàn hồi bằng M
c
.
GĐ 2: Cả 2 khối lượng cùng ch/đg đến lúc kết thúc tác động của
momen phát động M
n
– M
c
.
GĐ 1
);
1
1(
1
1
2
1
2
1
dt
d
Mk
dt
d
J
o
n
;0;0;0
1
1
dt
d
t
;cossin
1
k
M
qtBeqtAe
n
ytyt
(39)
(40)
Kết thúc gđ 1
;;
1
k
M
tt
c
o
);sin(cos
oo
yt
n
cn
qt
q
y
qte
M
MM
o
(41)
(41) t
o
;
(40)
;sin
)(
1
22
o
yt
n
tt
qte
kq
qyM
dt
d
o
o
(42)
2
1
2
1
1
J4
;
J2
o
n
o
n
M
J
k
q
M
y
12
GĐ 2.
Nghiệm của (35) có dạng (15) với điều kiện ban đầu (tính
từ đầu gđ 2: t = 0; φ = M
c
/k.
;sin
)(
22
1
o
yt
n
tt
qte
kq
qyM
dt
d
dt
d
o
o
);sin(cos)(
22
2
1
2
2
2
oo
yt
n
tt
qt
q
y
qteqy
k
M
dt
d
dt
d
o
o
(43)
Đkban đầu + đk
t
DB
k
M
A
k
M
cc
;
21
]cos[
)(
2
22
21
utee
uzx
z
ztxt
;sin]cos[
])[(
)()(
22
222
k
M
uteutee
uzxu
xzuzx
c
ztztxt
(44)
13
]cos[
)(
)2(
)(
22
2112
utee
uzx
zk
kM
ztxt
;sin]cos[
])[(
)]()([
22
222
c
ztztxt
Muteutee
uzxu
xzuzxk
m
xt
ez
uzx
k
M )2(
)(
22
max
12
;
)]()([)2(
22
222222
c
zt
M
uz
xzuzxzu
e
m
(45)
(46)
;
)]()([)2(
)]()([)2(1
2222
222
uzuzxuz
uxzuzxzz
arctg
u
t
m
(47)
14
3. Động lực học quá trình chất tải sau mở máy.
a/ Momen cản phụ thuộc vị trí
c
c
MM
2
φ
c
– góc quay ứng với tải trọng tĩnh
ổn định của khối lượng phụ động;
c
c
MM
2
2
2
,
J
tJ
1
1
,
k
Đối với đa số động cơ sau khi mở máy
trục đ/c có vận tốc gần như không đổi
;0
2
1
2
1
dt
d
J
;)(
2
21
2
2
2
2
c
c
Mk
dt
d
J
(a)
(b)
(48)
(a)
;
1
t
+ (b)
;
2
2
2
2
2
2
t
J
k
J
M
k
dt
d
c
c
ω - vận tốc góc ổn định của khâu chủ động sau khi mở máy
không tải.