Đề thi mẫu toán 12 luyện thi có đáp án (5)

ĐỀ MẪU CĨ ĐÁP ÁN

ƠN TẬP KIẾN THỨC
TỐN 12
Thời gian làm bài: 40 phút (Không kể thời gian giao đề)
-------------------------

Họ tên thí sinh: .................................................................
Số báo danh: ......................................................................
Mã Đề: 030.
Câu 1. Cho hình chóp
ngoại tiếp hình chóp đã cho.

có đáy là hình vng tâm

A.
.
Đáp án đúng: D

B.

.

Đáy

.

B.

.

là hình vng tâm

Vì

suy ra

.

D.

. Tính diện tích mặt cầu

.

có đáy là hình vng tâm

C.

D.
.

.

;

. Tính diện

.

nên

là tâm mặt cầu ngoại tiếp hình chóp

mặt cầu bằng:

, bán kính mặt cầu

. Diện tích

.

Câu 2. Nghiệm của phương trình
A.
.
Đáp án đúng: D

?

B.

.

C.

Giải thích chi tiết: Nghiệm của phương trình
A.
.
Lời giải

;

C.

Giải thích chi tiết: Cho hình chóp
tích mặt cầu ngoại tiếp hình chóp đã cho.
A.
Lời giải

.

B.

.

Điều kiện:

C.

.

D.

.

?

D.

.

.

Ta có:

.

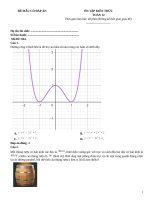
Câu 3. Cho hàm số
có đồ thị là
điểm cực trị đều nằm trên các trục tọa độ là
A.
B.
Đáp án đúng: D

. Tất cả các giá trị thực của tham số
C.

Giải thích chi tiết: Ta có
Tọa độ các điểm cực trị:

.

để

có 3

D.

Hàm số có ba điểm cực trị
,

và

1


Yêu cầu bài toán
Đối chiều điều kiện ta được

.

Câu 4. Trong khơng gian cho tam giác

vng tại

của hình nón có được khi quay tam giác
A.

và

xung quanh trục

.

. Tính diện tích xung quanh
.

B.

C.
Đáp án đúng: D

.

.

D.

Câu 5. Tập nghiệm của phương trình

.

là

A.
.
Đáp án đúng: B

B.

Câu 6. Tìm giá trị cực đại

của hàm số

.

C.

.

D.

.

.

A.

B.

C.
Đáp án đúng: B

D.

Giải thích chi tiết: Tìm giá trị cực đại
A.
B.
Lời giải
- Tập xác định:

C.

của hàm số

- Vậy
Câu 7.

=

.

.

= 1.

Cho hàm số bậc bốn
,

,

.

D.

- Ta có:
- Ta có BBT:

điểm

,

thỏa mãn

có đồ thị là đường cong trong hình vẽ. Biết hàm số
. Gọi

đạt cực trị tại ba

là diện tích của hình phẳng được tơ đậm và

là diện tích

2


của hình phẳng được gạch chéo trong hình vẽ. Biết
biểu thức
bằng

A.
.
Đáp án đúng: D

B.

.

Giải thích chi tiết: Tịnh tiến đồ thị hàm số
thấy diện tích

Từ đồ thị ta có

,

khơng thay đổi. Đồ thị

và

C.

với

.

. Khi đó, giá trị của

D.

sang trái sao cho điểm cực trị
chuyển thành đồ thị hàm số

.

trùng với gốc tọa độ. Ta
.

là ba điểm cực trị của hàm số
,(

)
.

Đồ thị hàm số đi qua điểm

.
3


Có

.
.

Mà

(thoả mãn). Suy ra

.

Khi đó

.
→

→

→

→

Câu 8. Trong khơng gian Oxyz , cho hai vectơ u =(1 ; 3 ;−2) và v =(2; 1 ;−1). Tọa độ của vectơ u −v là
A. (3 ; 4 ;−3).
B. (−1 ; 2;−3).
C. (1 ;−2; 1).
D. (−1 ;2;−1).
Đáp án đúng: D
Câu 9. Cho hình chóp
, điểm
khối tứ diện

có đáy là tam giác

thuộc cạnh
bằng

A.
.
Đáp án đúng: B
Giải thích chi tiết:
Lời giải

sao cho

B.

.

vng cân tại
, điểm

C.

thuộc cạnh

.

,

,

vng góc với đáy,

sao cho

D.

. Thể tích của

.

4


Áp dụng cơng thức tỉ số thể tích, ta có:
và
Nhân

và

.

theo vế, ta được

.

Mà

.

Từ

và
Câu 10.

.

Tập nghiệm của bất phương trình
A.
C.
.
Đáp án đúng: A

.

là
B.
D.

.
.
5


Câu 11.
Cho hàm số

liên tục trên

và có đồ thị như hình vẽ dưới đây

Tập hợp tất cả các giá trị thực của tham số

để phương trình

có nghiệm thuộc nữa khoảng

là
A.

.

B.

C.
.
Đáp án đúng: D

D.

Giải thích chi tiết: Đặt
Với

.
.

;

ta có bảng biến thiên của hàm số

.

Với
Từ đồ thị ta có:
Vây để phương trình
Câu 12. Họ ngun hàm của hàm số

có nghiệm thì

.
là

6


A.

B.

C.
Đáp án đúng: A

D.

Câu 13. Cho biểu thức

với

A.
.
Đáp án đúng: D

B.

.

. Biểu thức

C.

Giải thích chi tiết: Cho biểu thức
A.
. B.
Hướng dẫn giải

. C.

Ta có:
Vậy chọn đáp án A.

. Khi đó:

Câu 14. Trong mặt phẳng
A. 1.
Đáp án đúng: A

.

cho
B. 2.

tọa độ điểm

A.
C.
Đáp án đúng: B
Câu 17.

sao cho

D.

.

với

. Biểu thức

có giá tri là

.

để phương trình

có đúng ba

C. 0.

, cho các điểm

D. 3.

,

,

. Tìm

là hình bình hành.

.

B.

.

D.

Hàm số nào sau đây đồng biến trên

.

. Tích vơ hướng của 2 vectơ
là:
C. 3.
D. 4.

Câu 15. . Tích các giá trị của tham số
nghiệm phân biệt là?
A. 2.
B. .
Đáp án đúng: D
Câu 16.

Trong không gian với hệ tọa độ

D.

có giá tri là

.
.

và

7


A.

C.
Đáp án đúng: D

.

Câu 18. Giá trị của tích phân
A.
.
Đáp án đúng: D

B.

B.

.

.

Đặt

.

D.

.

là
C.

Giải thích chi tiết: Giá trị của tích phân
A.
.
Hướng dẫn giải

B.

; đặt

.

D.

.

là
C.

.

ĐS:

D.

.

.

Chú ý: Phân tích
, rồi đặt
sẽ tính nhanh hơn.
x
+
y
+1=0
Câu 19. Một vật chuyển động theo quy luật
với t (giây) là khoảng thời gian tính từ khi vật bắt đầu
chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời
gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là bao nhiêu ?
A. 4
B. 9
x=1+ t
C. y =−2
D. 243( m/ s)
z=3−t

Đáp án đúng: B
Câu 20.

{

Xét

là số thực lớn hơn 0 và khác 1. Phát biểu nào sau đây đúng?

A.
C.

.
.

B.
D.

.
.
8


Đáp án đúng: C
Giải thích chi tiết: Theo cơng thức ngun hàm ta có đáp án
B.
Câu 21. Cho hình nón có bán kính đáy r =4 cm , đường sinh l=5 cm . Tính chiều cao hình nón.
A. 1 cm
B. 3 cm
C. 4 cm

D. 2 cm
Đáp án đúng: B
Câu 22.
Cho 4 số thực

là 4 số hạng liên tiếp của một cấp số cộng. Biết tổng của chúng bằng 4 và tổng bình

phương của chúng bằng 24. Tính

.

A.

B.

C.
Đáp án đúng: C
Câu 23.
Biết

D.

là một nguyên hàm của hàm số

trên

A.

. Khi đó

bằng

B.

C.
Đáp án đúng: C
Câu 24.

D.

Sử dụng mảnh inox hình chữ nhật
có diện tích bằng
và cạnh
để làm một thùng đựng
nước có đáy, khơng có nắp theo quy trình như sau: Chia hình chữ nhật
thành hai hình chữ nhật
và
, trong đó phần hình chữ nhật
được gị thành phần xung quanh hình trụ có chiều cao bằng
; phần hình chữ nhật
được cắt ra một hình trịn để làm đáy của hình trụ trên. Tính gần đúng giá trị
để thùng nước trên có thể tích lớn nhất.

A.
.
Đáp án đúng: C

B.

.

C.

Giải thích chi tiết: Ta có
Gọi
Do đó

.

D.

.

là bán kính đáy hình trụ inox gị được, ta có chu vi hình trịn đáy bằng
;

.

Thể tích khối trụ inox gò được là

.

Xét hàm số

.

.

.
9

;
Vậy

và

đồng biến trên khoảng

Suy ra
Từ đó ta có thể tích

.

và nghịch biến trên khoảng

.

.
lớn nhất khi và chỉ khi

lớn nhất

.

Câu 25. Trong khơng gian
, cho điểm
và đường thẳng
qua
, vng góc với và cắt

có phương trình là

A.
.
Đáp án đúng: A

B.

.

C.

Câu 26. Cho hình trụ có bán kính đường trịn đáy là
trụ bằng
A.
.
Đáp án đúng: C

B.

.

. Đường thẳng đi

.

D.

, chiều cao
C.

.

. Khi đó diện tích tồn phần hình

.

D.

Giải thích chi tiết: Diện tích tồn phần của hình trụ là
Câu 27.

.
.

Một nhà nghiên cứu đã tiến hành thực nghiệm như sau. Ông ước tính rằng sau thời gian giờ kể từ lúc
nhiệt độ của một thành phố nào đó cho bởi hàm
của thành phố giữa

sáng và

đêm,

. Hãy tính nhiệt độ trụng bình

chiều.

A.

B.

C.
Đáp án đúng: C
Giải thích chi tiết:
Vì 6 giờ sáng và 4 giờ chiều tương ứng với

D.

và

. Như vậy, nhiệt độ trung bình của thành phố giữa 6

giờ sáng và 4 giờ chiều chính là giá trị trung bình của hàm nhiệt độ
trị trung bình ta có:

với

theo cơng thức tính giá

Vậy nhiệt độ trung bình trong khoảng thời gian đã cho là:
10


Câu 28. Cho lăng trụ đứng

có đáy

là khối trụ ngoại tiếp khối lăng trụ
A.
Đáp án đúng: C

Câu 29.

là tam giác vng cân tại A, AB=

. Diện tích xung quanh của

B.

C.

bằng
D.

Cho hàm số

Đồ thị hàm số

Hàm số

nghịch biến trên khoảng nào trong các khoảng sau?

A.
Đáp án đúng: A

Gọi

như hình vẽ bên dưới và

B.

C.

Câu 30. Biết

với

D.

là các số nguyên và phân số

là tối giản. Tính

.
A. .
Đáp án đúng: B

B.

.

C.

.

D.

.

Giải thích chi tiết: Đặt
Đổi cận:

.

Khi đó
.
Vậy

.

Câu 31. Tập nghiệm của bất phương trình
A.
.
Đáp án đúng: C

B.

là
.

C.

.

Câu 32. Tính thể tích khối trụ trịn xoay sinh ra khi quay hình chữ nhật
nó) quanh cạnh
A.

.

biết

D.

.

(kể cả các điểm bên trong của

.
B.

.

C.

.

D.

.
11


Đáp án đúng: C
Câu 33.
Trong không gian

, cho

A.

và

. Vectơ

.

B.

C.
.
Đáp án đúng: C

A.
Lời giải

.

D.

Giải thích chi tiết: Trong khơng gian
. B.

. C.

, cho
. D.

có tọa độ là

.

và

. Vectơ

có tọa độ là

.

.
⃗ ( 0 ;2 ;−1 ) , c⃗ = (3 ;−1 ; 5 ). Tìm tọa độ
Câu 34. Trong khơng gian với hệ trục tọa độ Oxyz , cho a⃗ =( 2 ;−3 ; 3 ), b=
của vectơ u⃗ =2 ⃗a +3 ⃗b−2 c⃗ .
A. (−2 ;2; 7 ).
B. ( 10 ;−2;13 ) .
C. (−2 ;2;−7 ).
D. (−2 ;−2;7 ).
Đáp án đúng: C
Câu 35. Có bao nhiêu số phức
A.
Đáp án đúng: D

thỏa mãn
B.

Câu 36. Cho số phức

và
C.

D.

. Biết rằng tồn tại các số phức

(trong đó

) thỏa mãn

. Tính
A.

.

B.

C.
.
Đáp án đúng: A

D.

Giải thích chi tiết: Đặt
Ta có

Đặt
phương trình).

Tìm được

.

.

lần lượt là các điểm biểu diễn cho các số phức

.

nên

thì

. Thay vào

(Nhân chéo vế với vế của

được

thỏa mãn.
12


Lúc này

Do

. Vậy

.

Câu 37. Một hình trụ có diện tích xung quanh bằng
trụ đó.

và bán kính đáy là

A.
.
Đáp án đúng: A

C.

B.

.

. Tính độ dài đường cao của hình

.

D.

.

Giải thích chi tiết: Diện tích xung quanh của hình trụ là:
Vậy độ dài đường cao của hình trụ đó là

.

Câu 38. Tìm giá trị lớn nhất của hàm số
A.

.

trên

.

.

B.

C.
.
Đáp án đúng: A

D.

Câu 39. Cho hàm số
A.

(

.

.
.

là tham số thực). Nếu
B.

C.
.

Đáp án đúng: C

Đặt

bằng

.

D.

Giải thích chi tiết: Xét:

thì

.

.
.

Đổi cận:

.

Khi đó:
.
Câu 40. Cho lăng trụ tam giác đều

có tất cả các cạnh bằng

. Cơ sin của góc giữa hai mặt phẳng

A.
.
Đáp án đúng: C

B.

.

Giải thích chi tiết: Xét hình lăng trụ tam giác đều
vẽ quy ước
( đơn vị ).

và
C.

.

là một điển thỏa mãn

bằng
.

D.

có tất cả các cạnh bằng

.
. Gắn hệ trục như hình

13

Gọi

là giao điểm của

và

.

Vì tam giác
là tam giác cân cạnh bằng
độ các điểm như hình vẽ.
Theo giả thiết ta có
Vậy tọa độ của điểm
Ta có mặt phẳng

nên ta suy ra độ dài các đường trung tuyến là

. Suy ra tọa

vậy
là:
có phương trình
14


Mặt khác mặt phẳng
Ta có:
Vậy

là mặt phẳng đi qua ba điểm

và

.

và
cơ sin góc tạo bởi hai mặt phẳng

và

.

là:

.
----HẾT---

15