Đề thi mẫu toán 12 luyện thi có đáp án (6)

ĐỀ MẪU CĨ ĐÁP ÁN

ƠN TẬP KIẾN THỨC
TỐN 12
Thời gian làm bài: 40 phút (Không kể thời gian giao đề)
-------------------------

Họ tên thí sinh: .................................................................
Số báo danh: ......................................................................
Mã Đề: 031.
Câu 1.
Trong khơng gian
A.

, cho

và

. Vectơ

.

B.

C.
.
Đáp án đúng: C

A.
Lời giải

. B.

.

D.

Giải thích chi tiết: Trong khơng gian
. C.

, cho
. D.

có tọa độ là

.

và

. Vectơ

có tọa độ là

.

.
Câu 2. Cho hàm số
với

liên tục trên

. Tính tích phân

A. .
Đáp án đúng: D

và thảo mãn

bằng
B.

.

C.

.

D.

.

Giải thích chi tiết:

.

1


Câu 3.
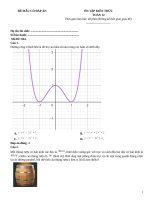
Đường cong ở hình bên là đồ thị của hàm số nào trong các hàm số dưới đây.

A.

.

C.
Đáp án đúng: B

B.
.

D.

Câu 4. Đạo hàm của hàm số
A.

B.
.

.

để hàm số

đạt

.

A.
.
Đáp án đúng: A

B.

.

C.

Giải thích chi tiết: [2] Tìm tất cả các giá trị của tham số
cực trị tại
A.

.

D.

Câu 5. Tìm tất cả các giá trị của tham số
cực trị tại

.

là:

.

C.
Đáp án đúng: D

.

.

để hàm số

D.

.
đạt

.
. B.

. C.

. D.

.
2


Lời giải
Ta có

,

Hàm số có hai cực trị khi

.

.
.

Câu 6. Cho các số dương
A.

, số thực

. Chọn khẳng định đúng trong các khẳng định sau?

.

B.

C.
.
Đáp án đúng: A

D.

Câu 7. Tập hợp các điểm biểu diễn số phức
A. Trục Ox trừ gốc tọa dộ.
C. Trục Oy trừ gốc tọa độ.
Đáp án đúng: C

sao cho

Ta có:

là điểm biểu diễn số phức
là số thực âm

sao cho

là số thực âm là:

.

là số thực âm. Mà

Câu 8. Cho hàm số
có đồ thị là
điểm cực trị đều nằm trên các trục tọa độ là
A.
B.
Đáp án đúng: C

. Tất cả các giá trị thực của tham số
C.

Giải thích chi tiết: Ta có

để

có 3

D.

Hàm số có ba điểm cực trị

Tọa độ các điểm cực trị:

Yêu cầu bài toán

Đối chiều điều kiện ta được

.

là số thực âm là:
B. Trục Oy.
D. Trục Ox.

Giải thích chi tiết: Tập hợp các điểm biểu diễn số phức
A. Trục Ox. B. Trục Ox trừ gốc tọa dộ.
C. Trục Oy. D. Trục Oy trừ gốc tọa độ.
Hướng dẫn giải
Gọi

.

,

và

.

Câu 9. Trong mặt phẳng
cho
A. 3.
B. 4.
Đáp án đúng: C
Câu 10. Xác định tập hợp các điểm

. Tích vơ hướng của 2 vectơ

C. 1.

là:
D. 2.

trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện:

.
A. Hình trịn tâm I(-1;-1), bán kính R = 1 (kể cả những điểm nằm trên đường trịn).
B. Hình trịn tâm I ¿ ;-1), bán kính R = 1.
3


C. Đường trịn tâm I(-1;-1), bán kính R = 1.
D. Đường trịn tâm I ¿ ;-1), bán kính R = 1.
Đáp án đúng: A
Giải thích chi tiết: Xác định tập hợp các điểm

trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều

kiện:
.
A. Đường tròn tâm I(-1;-1), bán kính R = 1.
B. Hình trịn tâm I ¿ ;-1), bán kính R = 1.
C. Hình trịn tâm I(-1;-1), bán kính R = 1 (kể cả những điểm nằm trên đường trịn).
D. Đường trịn tâm I ¿ ;-1), bán kính R = 1.
Hướng dẫn giải
Gọi

là điểm biểu diễn của số phức

trên mặt phẳng phức

.

Theo đề bài ta có
( Hình trịn tâm I(-1;-1) bán kính R = 1 và kể cả đường trịn

đó )
Trong câu này hs dễ nhầm trong q trình xác định tọa độ tâm đường trịn và hay quên dấu bằng sảy ra.
Câu 11. Tìm tập xác định
A.

của hàm số

.

.

B.

C.
Đáp án đúng: C

.

.

D.

Giải thích chi tiết: Do

.

nên hàm số đã cho xác định khi và chỉ khi

Vậy tập xác định cần tìm là:

.

Câu 12. Cho hình nón có độ dài đường sinh
nón đã cho bằng

và bán kính đáy bằng

A.
.
Đáp án đúng: C

B.

.

Giải thích chi tiết: Cho hình nón có độ dài đường sinh
của hình nón đã cho bằng
A.
. B.
Lời giải

. C.

. D.

C.

.
. Diện tích xung quanh của hình

.
và bán kính đáy bằng

D.

.

. Diện tích xung quanh

.

Ta có, diện tích xung quanh của hình nón
.
⃗ ( 0 ; 2 ;−1 ) , c⃗ = (3 ;−1 ; 5 ). Tìm tọa độ
Câu 13. Trong khơng gian với hệ trục tọa độ Oxyz , cho a⃗ =( 2 ;−3 ; 3 ), b=
của vectơ u⃗ =2 ⃗a +3 ⃗b−2 c⃗ .
A. ( 10 ;−2;13 ) .
B. (−2 ; 2;−7 ).
C. (−2 ;−2;7 ).
D. (−2 ;2; 7 ).
Đáp án đúng: B
Câu 14. Cho hình lập phương ABCD.A’B’C’D’. Tìm số đo của góc giữa mặt phẳng (BCD’A’) và mặt phẳng

(ADC’B’) ?
4


A.
Đáp án đúng: D

B.

Câu 15. Trong khơng gian
có phương trình

A.

C.
, cho hai điểm

.

C.
.
Đáp án đúng: B
Giải thích chi tiết: Trong khơng gian
điểm ,
có phương trình

A.
Lời giải

.

Ta có

B.

.

D.

,

. Đường thẳng

B.

.

D.

.

, cho hai điểm

C.

,

.

đi qua hai điểm

. Đường thẳng

D.

,

đi qua hai

.

.

Phương trình đường thẳng

có vectơ chỉ phương

và đi qua điểm

có phương trình

tham số là:
.
Câu 16. Một vật chuyển động theo quy luật x + y +1=0 với t (giây) là khoảng thời gian tính từ khi vật bắt đầu
chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời
gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là bao nhiêu ?
A. 9
B. 4
x=1+ t
C. 243( m/ s)

D. y =−2
z=3−t
Đáp án đúng: A

{

Câu 17. Cho lăng trụ đứng

có đáy

là khối trụ ngoại tiếp khối lăng trụ
A.
Đáp án đúng: B
Câu 18. Cho hình chóp

là tam giác vng cân tại A, AB=

. Diện tích xung quanh của

B.

bằng

C.
có đáy là hình chữ nhật,

. Tính thể tích khối chóp

Gọi

D.
,

,

,

vng góc với

.
5


A.

(đvtt).

B.

(đvtt).

C.
(đvtt).
D.
(đvtt).
Đáp án đúng: A
Câu 19. Cho hình lập phương ABCD . A ' B ' C ' D ' . Góc giữa hai mặt phẳng ( AA ' B ' B) và ( BB' D ' D ) là
A. ^
B. ^
C. ^

D. ^
ABD '
ADB
A ' BD '
DD ' B
Đáp án đúng: B
Câu 20.

bằng

A.

.

B.

.

.

D.

.

C.
Đáp án đúng: A
Giải thích chi tiết:
A.
Lời giải

bằng

. B.

. C.

. D.

.

Đặt
Đổi cận:

.
.

Câu 21. Cho hình chóp
cầu ngoại tiếp hình chóp đã cho.
A.
.
Đáp án đúng: A

có đáy là hình vng tâm

B.

.

Giải thích chi tiết: Cho hình chóp
tích mặt cầu ngoại tiếp hình chóp đã cho.

A.
Lời giải
Đáy

.

B.

là hình vng tâm

Vì
mặt cầu bằng:

suy ra

.

C.

.

;

C.

.

có đáy là hình vng tâm
.

D.

. Tính diện tích mặt
D.

.

.

;

. Tính diện

.

nên

là tâm mặt cầu ngoại tiếp hình chóp

, bán kính mặt cầu

. Diện tích

.
→

→

→

→

Câu 22. Trong khơng gian Oxyz , cho hai vectơ u =(1 ;3 ;−2) và v =( 2; 1 ;−1). Tọa độ của vectơ u −v là
A. (−1 ;2;−3).
B. (−1 ; 2;−1).
6


C. (3 ; 4 ;−3).
Đáp án đúng: B

D. (1 ;−2; 1).

Câu 23. Cho
A. 1.
Đáp án đúng: C

. Có bao nhiêu giá trị nguyên của
B. 5.
C. 3.

để

?
D. 2.

Giải thích chi tiết: (Thi thử Lômônôxốp - Hà Nội 2019) Cho
của để
?
Câu 24. Trong khơng gian cho tam giác

vng tại

của hình nón có được khi quay tam giác
A.

.

Câu 25. Cho hàm số
A.

B.

.

D.

.

.

D.

Giải thích chi tiết: Ta có
Vậy

. Tính diện tích xung quanh

.

B.

C.
.
Đáp án đúng: D

.

nên hàm số nghịch biến trên

.

.

Câu 26. Tập nghiệm của bất phương trình
A.
Đáp án đúng: C

là

B.

C.

Câu 27. Cho hàm số

(

.

D.

là tham số thực). Nếu
B.

C.
.
Đáp án đúng: D

D.

Giải thích chi tiết: Xét:
Đặt

và

. Mệnh đề nào dưới đây là đúng?

.

A.

,

xung quanh trục

.

C.
Đáp án đúng: C

. Có bao nhiêu giá trị ngun

thì

bằng

.
.

.
.
7


Đổi cận:

.

Khi đó:
.
Câu 28. Cho

và

Khẳng định nào sau đây sai ?

A.

B.

C.
Đáp án đúng: A

D.

Câu 29. Tập nghiệm của phương trình

là

A.
.
Đáp án đúng: B
Câu 30.

B.

Cho hình chóp

có đáy là hình vng cạnh

mặt phẳng

.

một góc

C.

C.

.
Đáp án đúng: C
Giải thích chi tiết: Cho hình chóp

A.
Lời giải

. B.

D.

,

.

vng góc với đáy,

tạo với

. Tính thể tích khối chóp

A.

tạo với mặt phẳng

.

B.

.

D.

.

có đáy là hình vng cạnh
một góc

. C.

,

vng góc với đáy,

. Tính thể tích khối chóp

. D.

+) Do ABCD là hình vng cạnh a nên:
+) Chứng minh được
+) Đặt

góc giữa SC và (SAB) là

.

. Tam giác SBC vuông tại B nên
8

Ta được:
(Đvtt).

.Vậy

Câu 31. Trong không gian
, cho điểm
và đường thẳng
qua
, vng góc với và cắt
có phương trình là

A.
.
Đáp án đúng: A

B.

Câu 32. Trong không gian

A.
.
Đáp án đúng: B

.

, đường thẳng

B.

Giải thích chi tiết: Trong khơng gian

C.

. Đường thẳng đi

.

D.

.

có phương trình tham số là

.

C.
, đường thẳng

.

D.

.

có phương trình tham số là

A.
.
B.

.
C.
.
D.
.
Lời giải
Câu 33. Với a là số thực dương tùy ý, log 5 ( 5 a ) bằng
A. 5+ log 5 a .
B. 1−log 5 a.
C. 1+log5 a .
D. 5−log 5 a.
Đáp án đúng: C
Câu 34.
Người ta muốn xây một bồn chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết chiều dài, chiều
rộng, chiều cao của khối hộp đó lần lượt là 5m, 1m, 2m, chỉ xây 2 vách (hình vẽ bên). Biết mỗi viên gạch có
chiều dài 20cm, chiều rộng 10cm, chiều cao 5cm. Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây bồn
đó và thể tích thực của bồn chứa bao nhiêu lít nước? (Giả sử lượng xi măng và cát khơng đáng kể )

A.

lít

B.

viên

lít

C.
viên

lít
Đáp án đúng: B
Giải thích chi tiết: chọn A

D.

viên

lít

Gọi

viên

là thể tích khối hộp chữ nhật

Ta có :
9


Thể tích mỗi viên gạch là
Số viên gạch cần sử dụng là

viên
Thể tích thực của bồn là :
Câu 35. Tập nghiệm của bất phương trình
A.

.

là
B.

C.
.
Đáp án đúng: D

.

D.

.

Câu 36. Tính thể tích khối trụ trịn xoay sinh ra khi quay hình chữ nhật
nó) quanh cạnh

biết

.

A.
.
Đáp án đúng: B
Câu 37. Biết rằng

B.

.

là một nguyên hàm trên

Giá trị nhỏ nhất của hàm số
A.
.
Đáp án đúng: D

(kể cả các điểm bên trong của

C.

.

D.

của hàm số

.

và thỏa mãn

.

bằng
B.

.

C.

.

D.

.

Giải thích chi tiết: Ta có

Từ bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số

bằng
10


Vậy giá trị nhỏ nhất của hàm số

bằng

.

Câu 38. Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
thuộc hai đáy của khối trụ. Biết
,
. Tính thể tích của khối trụ:
A.

.

B.

C.

.
Đáp án đúng: D

D.

Câu 39. ~ Giá trị cực tiểu của hàm số
A.
.
Đáp án đúng: B

.
.

.

C.

.

Giải thích chi tiết: [Mức độ 1] Giá trị cực tiểu của hàm số

Tập xác định

.

D.

D.

.

bằng

.

.

Ta có
Bảng biến thiên:

.

Từ bảng biến thiên ta thấy giá trị cực tiểu của hàm số bằng
Câu 40. Cho hình lăng trụ đứng
,
. Thể tích khối lăng trụ
A.
.
Đáp án đúng: D

và

bằng

B.

A.
.
B.
.

C.
Lời giải
FB tác giả: Danh Được Vũ
Mail:

có

B.

có đáy
là
.

.
là tam giác vng tại
C.

.

. Biết rằng
D.

,

.

----HẾT---

11