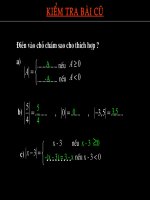Tiet 64 - phuong trinh chua dau gia tri tuyet doi

Giải bất phương trình và biểu diễn tập
Giải bất phương trình và biểu diễn tập
nghiệm trên trục số: -3(x + 2) < x - 1 .
nghiệm trên trục số: -3(x + 2) < x - 1 .
///////////(
0-1,25
⇔ - 4x < 5
-3(x+2) < x - 1
⇔ - 3x - 6 < x- 1
⇔ - 3x -x < 6 - 1
⇔ (- 4x ) :(- 4) > 5:(- 4)
⇔ x > -1,25
-3(x+2) < x - 1
⇔ -3x -6 < x- 1
⇔ -6 + 1 < 3x + x
⇔ -5 < 4x
⇔ -5:4 < 4x:4
⇔ -1,25 < x
Nghiệm của bất phương trình là x > -1,25
Biểu diễn tập nghiệm trên trục số:

Chúng ta đã biết giải các phơng trình dạng
( )
2 2 1 1;x x + =
( 2)(2 3) 0;x x
+ =
( ) ( ) ( )
2
2 3 2 2 1 3

x x x
x x x x
+ =
+ +
Còn các phơng trình dạng
3 4;x x= +
3 9 2 ;x x
=
5 3 1x x+ = +
Đa về phơng trình không
chứa dấu giá trị tuyệt đối
bằng cách nào?

1. Nhắc lại về dấu giá trị tuyệt đối:
| a | = a khi a ≥ 0 ; | a | = −a khi a < 0.

|5| = 5 ; |0| = 0; |-3,5| = 3,5

| a | = a khi a ≥ 0 ; | a | = −a khi a < 0.
Bỏ dấu giá trị tuyệt đối và rút gọn :
a) A = |x − 3| + x − 2 khi x ≥ 3;
b) B = 4x + 5 + |−2x| khi x > 0.
Ví dụ 1:
a) Khi x ≥ 3, ta có x − 3 ≥ 0 nên |x − 3| = x −
3. Vậy: A = x − 3 + x − 2 = 2x − 5.
b) Khi x > 0, ta có −2x < 0 nên |−2x| = −(−2x) =
2x Vậy: B = 4x + 5 + 2x = 6x + 5.

Rót gän c¸c biÓu thøc:
?1

3 7 4C x x
= − + −
0x ≤
a)
khi
5 4 6D x x= − + −
6x <
b)
khi
Khi
0,x
≤
a)
ta cã
3 0x
− ≥
nªn
3 3 .x x
− =−
VËy
3 7 4 4 4.C x x x
=− + − = −
Khi
6,x
<
b)
ta cã
6 0x
− <
nªn

6 6 .x x
− = −
VËy
5 4 6 11 5D x x x
= − + − = −
Gi¶i:
| a | = a khi a ≥ 0 ; | a | = −a khi a < 0.

2. Giải một số phơng trình chứa dấu giá trị tuyệt đối
Giải:
hay
Ta có
khi
3 3x x=
0x

3 0x
khi hay
3 3x x=
3 0x
<
0x <
Vậy để giải phơng trình (1) ta quy về giải hai phơng trình sau:
a) Phơng trình 3x = x + 4 với điều kiện x 0,
Ví dụ 2. Giải phơng trình
3 4x x= +
(1)
Ta có 3x = x + 4 2x = 4 x = 2
Giá trị x = 2 thỏa mãn điều kiện x 0, nên 2 là nghiệm của phơng trình (1).
b) Phơng trình -3x = x + 4 với điều kiện x < 0,

Ta có -3x = x + 4 -4x = 4 x = -1
Giá trị x = -1 thỏa mãn điều kiện x < 0, nên -1 là nghiệm của phơng trình (1).
Tập nghiệm của phơng trình (1) là S = {-1;2}
| a | = a khi a 0 ; | a | = a khi a < 0.

a
= a khi a 0
= -a khi a < 0
a
Ví dụ 3. Giải phơng trình
3 9 2x x =
(2)
hay
Ta có
khi
3 3x x =
3x

3 0x
Vậy để giải phơng trình (2) ta quy về giải hai phơng trình sau:
a) Phơng trình x - 3 = 9 - 2x với điều kiện x 3.
Ta có x - 3 = 9 - 2x 3x = 9 + 3 3x = 12 x = 4
b) Phơng trình -(x - 3) = 9 - 2x với điều kiện x < 3.
Ta có -(x - 3) = 9 - 2x -x + 3 = 9 - 2x x = 6
Tập nghiệm của phơng trình (2) là S = {4}
Giải:
hay
khi
3 ( 3)x x =
3x

<
3 0x <
Giá trị x = 4 thỏa mãn điều kiện x 3, nên 4 là nghiệm của phơng trình (2).
Giá trị x = 6 không thỏa mãn điều kiện x < 3, ta loại.
Giải các phơng trình:

Hoạt động nhóm
Giải các phơng trình:
a) x + 5 = 3x + 1 b) -5x = 2x + 21
Giải

Với x + 5 0 x -5
Ta có phơng trình :
x + 5 = 3x + 1 x = 2
(TMĐK )

Với x + 5 < 0 x < -5
Ta có phơng trình:
-(x+5) = 3x + 1 x = (loại)
Vậy tập nghiệm của PT đã cho
là S={2}
2
3


Nếu -5x 0 x 0
Ta có phơng trình :
-5x = 2x + 21 x=
-3( TMĐK )

Nếu -5x < 0 x > 0
Ta có phơng trình :
5x = 2x + 21 x = 7 (TMĐK)
Vậy tập nghiệm của PT đã cho là
S={-3;7}

?2

Bµi tËp 1: tr¾c nghiÖm
Kh¼ng ®Þnh nµo ®óng , kh¼ng ®Þnh nµo sai ?
1) = 4 x khi x < 4 –x-4
2) = 5x khi x > 0–-5x
3) = 4x khi x > 0–4x
4) = x - 5 khi x > 5 x-5
§óng
Sai
Sai
§óng

Chọn câu trả lời đúng:
Nghiệm của phương trình |x-2| = 18 - 3x là:
a)
x = 5
d)
x = 8
b) x = 5; x = 8
Một đáp số khác
c)
đúng
sai

sai
sai

Giải phơng trình x 2 = 7 2x
Giải:
Ta có: x 2 = x 2 khi x 2
x 2 = 2 x khi x < 2
a) Với x 2 ta có pt x 2 = 7 2x
3x = 9 x = 3(TMĐK)
b) Với x <2 ta có pt 2 x = 7 2x
x = 5 ( Loại )
Vậy pt đã cho có tập nghiệm là
S = { 3 }
Ta có: x 2 = x 2 khi x 2
x 2 = 2 x khi x < 2
+) Bỏ dấu giá trị tuyệt đối
với điều kiện kèm theo.
a) Với x 2 ta có pt x 2 = 7 2x
3x = 9 x = 3(TMĐK)
b) Với x <2 ta có pt 2 x = 7 2x
x = 5 ( Loại )
+) lập và giải các phơng
trình không chứa dấu gía trị
tuyệt đối với ĐK tơng ứng.
+) Kết luận.
Bài tập 2:

* Cách giải:
+) Bỏ dấu giá trị tuyệt đối với điều kiện kèm theo.
+) lập và giải các phơng trình không chứa dấu gía trị

tuyệt đối với ĐK tơng ứng.
+) Kết luận.

Giải phơng trình:
6 2 3x x
= +
Giải
hay
Ta có
khi
6 6x x =
6x

6 0x

Vậy để giải phơng trình (5) ta quy về giải hai phơng trình sau:
a) Phơng trình x - 6 = 2x + 3 với điều kiện x 6.
Ta có x - 6 = 2x + 3 x - 2x = 3 + 6 -x = 9 x = -9
b) Phơng trình 6 - x = 2x + 3 với điều kiện x < 6.
Ta có 6 - x = 2x + 3 -x - 2x = 3 - 6 -3x = -3 x = 1
Tập nghiệm của phơng trình (5) là S = {1}
Giá trị x = -9 khụng thỏa mãn điều kiện x 6, nên loai
Giá trị x = 1 thỏa mãn điều kiện x < 6, nên 1 là nghiệm của phơng trình (5).
6 ( 6) 6x x x = =
khi
6 0x
<
hay
6x
<

(5)
Bài tập 3:

Bài tập 4
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức
C = 3x + 7 + x 6 khi x < 6
Giải : Khi x < 6 , ta có x 6 < 0 nên
x 6 = 6 - x
Vậy C = 3x + 7 + 6 - x = 2x + 13

Bạn Nam giải bất phơng trình:
x 4 = 8 5x nh sau:
Giải:
a) Nếu x - 4 0 thì x 4 = x 4 nên ta có PT:
x 4 = 8 5x x + 5x = 8 + 4 x = 2
b) Nếu x - 4 < 0 thì x 4 = 4 - x nên ta có PT:
4 - x = 8 5x -x + 5x = 8 - 4 x = 1
Vậy tập nghiệm của PT đã cho là: S=
x 4x 4
(TMĐK)
(Loại)
x > 4x < 4
(Loại)
(TMĐK)
{ 2 }{ 1 }
Bài tập 5

Nối mỗi dòng ở cột bên trái với một dòng
ở cột bên phải để có kết quả đúng:
a) 2|x-1|-3 = -5 x = -2; x = -4

b) |x+3|-1 = 0 x = ; x = 5
c) |x+1|-3 = 2x x = ;x = -2
d) 2|x-1|-3 = x vô nghiệm
x=


3
4
−
3
4
−
3
1
−
Bµi tËp 6

•


Soạn bài tập 37 SGK.
Soạn bài tập 37 SGK.
•


Soạn bài tập 66, 67, 68 / 48 SBT
Soạn bài tập 66, 67, 68 / 48 SBT
•

Chuẩn bị “Ôn tập chương”, soạn câu hỏi SGK
Chuẩn bị “Ôn tập chương”, soạn câu hỏi SGK
/52
/52


1.Giải phương trình:
1.Giải phương trình:
a) |2x
a) |2x
−
−
5| = 2
5| = 2
−
−
x
x
b) 2|x + 1| + |x
b) 2|x + 1| + |x
−
−
3| = 6
3| = 6


2.Giải bất phương trình:
2.Giải bất phương trình:
|x
|x

−
−
1| < 9 + 3x
1| < 9 + 3x
Hướng dẫn về nhà
Hướng dẫn về nhà

•
Lập bảng xét dấu :
•
Với x<-5:
x
x+5

-2x+1
-5 0,5
0
++
-
0
-+
+
ta có: -x-5 - (1-2x) = x
⇔ -x+2x-x = 6

⇔ 0x = 6 : vô nghiệm
ta có: x+5 - (1-2x) = x ⇔ x+2x-x = -4

•
Với -5<x< 0,5:

⇔
⇔


x
x
= -2 :thỏa mãn -5 x < 0,5 nên là nghiệm của
= -2 :thỏa mãn -5 x < 0,5 nên là nghiệm của
(1)
(1)
≤
•
Với x ≥ 0,5:
ta có: x+5 + (1-2x) = x ⇔ -2x = -6


⇔
⇔


x
x
= 3 : thỏa mãn
= 3 : thỏa mãn
x
x


≥
≥

0,5 nên là nghiệm của (1)
0,5 nên là nghiệm của (1)
Vậy:Tập nghiệm của phương trình (1) là S ={-2;
3}.


Giải phương trình
Giải phương trình


|x+5| - |1-2x| = x (1)
|x+5| - |1-2x| = x (1)
-5
0
0,5

Gi¶i ph¬ng tr×nh:
2 1 5 3x x x− + + = −
§Ó gi¶i ph¬ng tr×nh trªn ta quy vÒ gi¶i hai ph¬ng tr×nh sau:
a) Ph¬ng tr×nh x - 2 + x + 1 = 5x - 3 víi ®iÒu kiÖn x ≥ 2.
0
2
-1
b) Ph¬ng tr×nh -(x - 2) + x + 1 = 5x - 3 víi ®iÒu kiÖn -1 ≤ x < 2.
c) Ph¬ng tr×nh -(x - 2) - (x + 1) = 5x - 3 víi ®iÒu kiÖn x < -1.