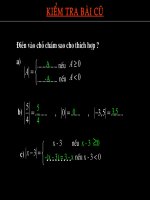phương trình chưa dấu giá trị tuyệt đối cực kỳ hay toán 8

Cuộc thi thiết kế bài giảng E – Learning

1. Nhắc lại về giá trị tuyệt đối
3
) 3
( 3)
x
a x
x
− ≥ ≥

− =

− −

neáu x - 3 0 hay x 3
neáu x - 3 < 0 hay x < 3
Hãy bỏ dấu giá trị tuyệt đối cho các biểu thức sau:
0
0
a a
a
a a
≥

=

− <

neáu

neáu
) 3
) 2
a x
b x
−
−
2
) 2
( 2 ) 2
x
b x
x x
− ≥ ≤

− =

− − =

neáu -2x 0 hay x 0
neáu -2x < 0 hay x > 0

Ví dụ 1: Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức
) 4 5 2 0b B x x khi x= + + − >
) 3 2 3
) 4 5 2 0
a A x x khi x
b B x x khi x
= − + − ≥
= + + − >

Khi x > 0 thì do đó
2 2x x− =
4 5 2 6 5B x x x= + + = +
Hãy thu gọn các biểu thức sau:
) 3 7 4 0
) 5 4 6 6
a C x x khi x
b D x x khi x
= − + − ≤
= − + − <

Khi thì nên
) 3 7 4 0
) 5 4 6 6
a C x x khi x
b D x x khi x
= − + − ≤
= − + − <
0x ≤
3 3x x− = −
3 7 4 4 4C x x x= − + − = −
Khi thì nên
6x <
6 ( 6)x x− = − −
5 4 6 11 5D x x x= − − + = −
Bài làm:

2. Giải một số phương trình chứa dấu giá trị tuyệt đối
3
3

( 3)
x
x
x
− ≥ ≥

− =

− −

neáu x - 3 0 hay x 3
neáu x - 3 < 0 hay x < 3
Xét ví dụ 1. Giải phương trình sau:
3 4x x= +
Xét ví dụ 2. Giải phương trình sau:
3 9 2x x− = −
Giải:
1: 3TH Khi x ≥
thì phương trình
3 9 2x x⇔ − = −
3 9 2x x− = −
2 9 3x x⇔ + = +
3 12 4x x⇔ = ⇔ =
(nhận)
2: 3TH Khi x <
thì phương trình
3 9 2
3 9 2
2 9 3 6
x x

x x
x x x
− = −
⇔ − = −
⇔ − + = − ⇔ =
(loại)
Vậy tập nghiệm của phương trình là
{ }
4S =

Phương pháp giải
•
Bỏ dấu giá trị tuyệt đối theo hai trường hợp
•
Đưa phương trình đề bài theo từng trường hợp
để giải
•
So sánh nghiệm thu được với điều kiện của
trường hợp đó xem có thỏa mãn không
•
Kết luận nghiệm của phương trình

Luyên tập
Bài 1: Giải các phương trình sau:
a) l x + 5 l = 3x + 1
b) l – 5x l = 2x + 21

Chú ý
•
Ngoài cách giải thông thường ở trên

chúng ta còn có cách giải khác như sau:
Nếu ta có phương trình lax+bl=cx+d
TH1: ax + b = cx + d nếu
0ax b+ ≥
TH1: ax + b = - cx - d nếu
0b+ <ax

Hướng dẫn về nhà
•
Biết cách bỏ dấu giá trị tuyệt đối của một biểu thức
•
Nắm vững phương pháp giải phương trình chứa dấu
giá trị tuyệt đối
•
Làm các bài tập 35, 36 a,b, 37 a,b
•
Chuẩn bị tiết học sau “Ôn tập chương IV”