Bài 1. Hàm số lượng giác (tiết 2)

CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
1.Tóm tắt kiến thức tiết 1
2.Kiểm tra bài tập đã làm ở nhà
Nháy chuột vào
Mục cần kiểm tra
BÀI 1
CÁC HÀM SỐ LƯỢNG GIÁC
(Tiết 2)
1) Các hàm số y = sinx và y = cosx
2) Các hàm số y = tan x và y = cotx
3) Về khái niệm hàm số tuần hoàn
Nháy chuột vào
Mục cần học
2)Hàm số y = tanx và y = cotx
a) Định nghĩa
b) Tính chất tuần hoàn
c) Sự biến thiên của hàm số y = tanx
d) Sự biến thiên của hàm số y = cotx
Nháy chuột vào
Mục cần học
2)Hàm số y = tanx và y = cotx
a) Định nghĩa
• Với mỗi số thực x mà cosx ≠ 0, tức là x ≠
k
2
π
+ π
ta xác định được số thực tanx =
sinx
cosx

Đặt D
1
= IR \
Quy tắc đặt tương ứng mỗi số x ∈D
1
với mỗi số thực
tanx = được gọi là hàm số tang, kí hiệu là y = tanx
sinx
cosx
k ,k Z
2
π
 
+ π ∈
 
 
Lý giải TXĐ của y = tanx
2)Hàm số y = tanx và y = cotx
a) Định nghĩa
• Với mỗi số thực x mà cosx ≠ 0, tức là x ≠
k
2
π
+ π
ta xác định được số thực tanx =
sinx
cosx
Đặt D
1
= IR \

Quy tắc đặt tương ứng mỗi số x ∈D
1
với mỗi số thực
tanx = được gọi là hàm số tang, kí hiệu là y = tanx
sinx
cosx
Vậy hàm số y = tanx có tập xác định D
1
ta viết
tan: D
1
→IR
x |→ tanx
k ,k Z
2
π
 
+ π ∈
 
 
Chuyển Slide
Lý giải TXĐ của y = tanx
2)Hàm số y = tanx và y = cotx
a) Định nghĩa
• Với mỗi số thực x mà sinx ≠ 0, tức là x ≠ kπ
ta xác định được số thực cotx =
cosx
sinx
Đặt D
2

= IR \
Quy tắc đặt tương ứng mỗi số x ∈D
2
với mỗi số thực
cotx = được gọi là hàm số côtang, kí hiệu là y = cotx
cosx
sinx
Vậy hàm số y = cotx có tập xác định D
2
ta viết
cot: D
2
→IR
x |→ cotx
{ }
k ,k Z
π ∈
Chuyển Slide Lý giải TXĐ của y = cotx
2)Hàm số y = tanx và y = cotx
a) Định nghĩa
Nhận xét: 1) Hàm số y = tanx là một hàm số lẻ
vì nếu x∈ D
1
thì -x∈ D
1
và tan(-x) = -tanx
2) Hàm số y = cotx là một hàm số lẻ
vì nếu x∈ D
2
thì -x∈ D

2
và cot(-x) = -cotx
MH :y = tanx lẻ MH: y = cotx lẻ Quay về mục chính
2)Hàm số y = tanx và y = cotx
b) Tính chất tuần hoàn
Có thể chứng minh được rằng:
T = π là số dương nhỏ nhất thỏa mãn: tan(x+T) = tanx,∀x∈D
1
T = π là số dương nhỏ nhất thỏa mãn: cot(x+T) = cotx,∀x∈D
1
Nhớ:
tan(x+kπ) = tanx , ∀x∈ D
1
,∀k∈Z
cot(x+kπ) = cotx , ∀x∈ D
2
,∀k∈Z
Ta nói hàm số y = tanx và y = cotx là những hàm số tuần hoàn
với chu kì π
MH : tính tuần hoàn
của y = tanx
MH : tính tuần hoàn
của y = cotx
Quay về mục chính
2)Hàm số y = tanx và y = cotx
c) Sự biến thiên của y = tanx
Khảo sát trên một chu kì: ( ) ⊂ D
1
=> tịnh tiến
phần đồ thị của chu kì này sang phải, sang trái các đoạn có

độ dài π,2π,3π… thì ta được toàn bộ đồ thị của hàm số y = tanx
;
2 2
π π
−
Chuyển Slide
2)Hàm số y = tanx và y = cotx
c) Sự biến thiên của y = tanx
;
2 2
π π
−
Đang xét hàm số y = tanx trên ( )
AT tanx=
t
x
o
A’ A
B
B’
M
T
Đây là trục tang
x
H6: Tại sao có thể khẳng định hàm số
y = tanx đồng biến trên mỗi khoảng
( ), k∈Z?
k ; k
2 2
π π

− + π + π
Hàm số y = tanx đồng biến trên ( )
;
2 2
π π
−
Vì
Hàm số y = tanx đồng biến trên ( )
và là hàm tuần hoàn chu kì π
;
2 2
π π
−
Đồ thị y = tanx
Tính đồng biến
của y = tanx
2)Hàm số y = tanx và y = cotx
c) Sự biến thiên của y = tanx
Xét đồ thị hàm số y = tanx trên một chu kì
x
y
0
2
π
−
2
π
Nhiều chu kì
2)Hàm số y = tanx và y = cotx
c) Sự biến thiên của y = tanx

Đang xét đồ thị hàm số y = tanx trên ba chu kì ( 0;π)
x
y
0
2
π
−
2
π
3
2
π
−
−π
π
3
2
π
Nhận xét Tóm tắt bài
2)Hàm số y = tanx và y = cotx
c) Sự biến thiên của y = tanx
Nhận xét:
1)Khi x thay đổi tên D
1
, hàm số y = tanx nhận mọi giá trị thực.
Ta nói tập giá trị của hàm số y = tanx là IR
2) Vì hàm số y = tanx là hàm số lẻ nên đồ thị của nó nhận
gốc tọa độ O làm tâm đối xứng.
3)Hàm số y = tanx không xác định tại x = .
k (k Z)

2
π
+ π ∈
Với mỗi k∈Z, đường thẳng vuông góc với trục hoành, đi qua
Điểm ( ) gọi là đường tiệm cận của đò thị hàm số
y = tanx
k ; 0
2
π
+ π
MH tiệm cận
Quay về mục chính
2)Hàm số y = tanx và y = cotx
d) Sự biến thiên của y = cotx
Hàm số y = cotx xác định tren tập D
2
= IR\ và tuần
hoàn chu kì π ,Ta khảo sát hàm số trên một chu kì (0;π)
{ }
k
π
y
x
0
π
2
π
Đồ thị y = cotx
Tính nghịch biến
của y = cotx

2)Hàm số y = tanx và y = cotx
d) Sự biến thiên của y = cotx
Hàm số y = cotx xác định trên tập D
2
= IR\ và tuần
hoàn chu kì π ,Quan sát đồ thị hàm số y = cotx trên ba chu kì
{ }
k
π
x
y
0
2
π
2
π
−
−π
π
3
2
π
2π
Tóm tắt bài
Thư giãn
2)Hàm số y = tanx và y = cotx
d) Sự biến thiên của y = cotx
Ghi nhớ
Hàm số y = tanx
Hàm số y = cotx

-TXĐ: D = R\ -TXĐ: D = R\
-Tập giá trị: IR
-Tập giá trị: IR
-Là hàm số lẻ
-Là hàm số lẻ
-H/s tuần hoàn chu kì π
-H/s tuần hoàn chu kì π
-Đồng biến trên mỗi khoảng
( )
k2 ; k2
2 2
π π
− + π + π
-Nghịch biến trên mỗi khoảng
( kπ ;π +kπ)
k ,k Z
2
π
 
+ π ∈
 
 
{ }
k ,k Z
π ∈
-
Đồ thị nhận mỗi đường thẳng
x = làm
một đường tiệm cận.
k ,k Z

2
π
+ π ∈
-
Đồ thị nhận mỗi đường thẳng
x = kπ , k∈Z làm tiệm một
đường tiệm cận.
MH: y = tanx MH: y = cotxKết thúc tiết 2
Ghi nhớ 1
Hàm số y = sinx
Hàm số y = cosx
-Tập xác định: D = R -Tập xác định: D = R
-Tập giá trị: [-1;1]
-Tập giá trị: [-1;1]
-Là hàm số lẻ
-Là hàm số chẵn
-H/s tuần hoàn chu kì 2π
-H/s tuần hoàn chu kì 2π
-Đồng biến trên mỗi khoảng
( )
k2 ; k2
2 2
π π
− + π + π
-Nghich biến trên mỗi khoảng
( )
3
k2 ; k2
2 2
π π

+ π + π
-Đồng biến trên mỗi khoảng
( )
k2 ; k2−π + π π
-Nghich biến trên mỗi khoảng
( )
k2 ; +k2π π π
Đến ghi nhớ 2 Về KTBC
Tóm tắt bài
•• •
•
••••
2
π
−
•
−π
3
2
π
−
2− π
2
π
•
π
3
2
π
2π

x
y
1
-1
•
0
•
•
•
•
Đồ thị y = sinx màu vàng.
Quay về đn y = cotx
sinx = 0 tại x = kπ mà cotx =
cosx
sinx
Nên y = cotx có tập xác định D
2
= IR \ kπ
•• •
•
••••
2
π
−
•
−π
3
2
π
−

2− π
2
π
•
π
3
2
π
2π
x
y
1
-1
Đồ thị hàm số y = cosx
Quay về đn y = tanx
cosx = 0 tại x =
k
2
π
+ π
mà tanx =
sinx
cosx
Nên tập xác định của y = tanx là D
1
= IR \
k
2
π
 

+ π
 
 
o
A’
A
B’
B
T
r
ụ
c

t
a
n
g
x
M
x
M
x
M
T
x
M
T
M
x
T

M
x
T
M
x
T
M
x
T
M
x
T
M
x
x
M
Hãy quan sát khi x tăng
trên ( -π/2 ; π/2) thì
tung độ điểm T tăng
để biết tan x tăng ?=>
hàm số y = tanx tăng ?
Về tính đồng biến
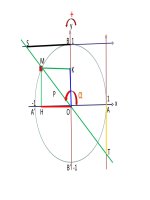
Hãy quan sát khi x tăng trên ( 0 ;
π) thì hoành độ điểm C giảm cho
biết cotx giảm ?=> hàm số y = cotx
giảm trên ( 0; π )?
o
A’
A
B’

B
Trục cotang
x
M’
C
M
x
M
x
C
M
x
C
C
M
x
C
M
x
M
x
Về tính nghịch biến biế
của y = cotx
o
A’
A
B’
B
T
r

ụ
c

t
a
n
g
M
x
M’
-x
T
T’
AT
AT'
AT' AT= −
= tanx
= tan (- x)
Nên tan (-x) = - tanx
=> Hàm số y = tanx là hàm số lẻ
Quay về t/c chẵn lẻ
o
A’
A
B’
B
Trục cotang
M
x
M’

-x
C
C’
BC
BC'
BC' BC= −
= cotx
= - cotx
=> cot(-x) = - cotx => hàm số y = cotx là hàm số lẻ
Quay về t/c chẵn lẻ