Đề thi học kì II môn toán 7(có đáp án)

Trường:
Họ tên:
Lớp: 7
KIỂM TRA CHẤT LƯỢNG HỌC KỲ II
Năm học: 2014-2015
Môn thi: TOÁN - Lớp 7
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ SỐ 2:
Câu 1 (2,0 điểm)
Điểm kiểm tra môn Toán của 30 bạn trong lớp 7B được ghi lại như sau:
8 9 6 5 6 6 7 6 8 7
5 7 6 8 4 7 9 7 6 10
5 3 5 7 8 8 6 5 7 7
a. Dấu hiệu ở đây là gì?
b. Lập bảng tần số?
c . Tính số trung bình cộng và tìm mốt của dấu hiệu.
Câu 2 (1,5 điểm)
a) Tìm các đơn thức đồng dạng trong các đơn thức sau:
3 3 2 3
1
5x y ; 2xy ; x y ; x y ; 4xy
4
−
b) Thu gọn, cho biết hệ số và tìm bậc của đơn thức sau:
( )
2
2xy. 3x y−
Câu 3 (2,0 điểm)
Cho hai đa thức f(x) = 5x
2
+ 4x – 8 ; g(x) = x

2
– 2x
a) Tính giá trị của đa thức f(x) tại x = - 2
b) Tính f(x) + g(x)
c) Tìm nghiệm của đa thức g(x)
Câu 4 (3,0 điểm)
Cho
ABC
∆
vuông tại A. Đường phân giác BD (DЄ AC). Kẻ DH vuông góc với BC (H
∈

BC). Gọi K là giao điểm của BA và HD.
Chứng minh:
a) AD = HD
b) BD
⊥
KC
c)
·
DKC
=
·
DCK
d) 2( AD+AK ) > KC
Câu 5 (1,5 điểm)
Cho tam giác DEF vuông tại D, có DE = 3cm và DF =
27
cm. Gọi I là trung điểm của EF.
a) Tính độ dài cạnh EF

b) Chứng minh rằng tam giác IDE là tam giác đều.
HƯỚNG DẪN CHẤM ĐỀ ĐỀ XUẤT TOÁN 7
HỌC KÌ II NĂM HỌC 2014 – 2015
(Hướng dẫn chấm có 02 trang)
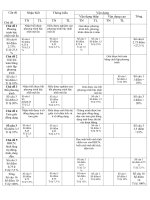
Câu Đáp án Điểm
1
a Dấu hiệu: Điểm kiểm tra môn toán 0,5
b
Bảng “tần số”:
Điểm (x) 8 9 6 7 5 3 10 4
Tần số (n) 5 2 7 8 5 1 1 1 N =30
0,5
Số trung bình cộng:

6,6
30
1.41.101.35.58.77.62.95.8
=
+++++++
=X
0,25
0,25
b Mốt của dấu hiệu: M
0
= 7 0,5
2
a Các đơn thức đồng dạng là:
3 3
5x y ; x y
0,5

b
+ Thu gọn:
( )
[ ]
( )
( )
2 2
3 2
2xy. 3x y 2.( 3) x.x y.y
6x .y
− = −
= −
+ Hệ số của đơn thức : - 6
+ Bậc của đơn thức : 5
0,25
0,25
0,25
0,25
3
a
f(-2) = 5.(-2)
2
+ 4.(-2) – 8 = 4
0,25
0,25
b
f(x) + g(x) = 5x
2
+ 4x – 8 + x
2

– 2x
= 6x
2
+ 2x - 8
0,25
0,25
0,5
c
Nghiệm của đa thức g(x) = x
2
– 2x là x = 0
và x = 2 0,25
0,25
4
a
a) Chứng minh được: ABD=  HBD (cạnh huyền - góc nhọn).
=>AD=HD ( 2 cạnh tương ứng)
0,25
0,25
b b) Xét BKC có D là trực tâm => BD là đường cao ứng cạnh KC
=> BD vuông góc KC
0,25
A
B
C
D
H
K
4
0,25

c
c) AKD = HCD ( cạnh góc vuông- góc nhọn kề)
=>DK= DC =>DKC cân tại D
=>
·
DKC
=
·
DCK
0,25
0,25
0,25
d
AKD= HCD =>AK= HC (1)
AD = HD (c/m câu a) (2)
Và : AD+AK > KD, DH+HC > DC (BĐT tam giác) (3)
Từ (1),(2),(3) =>2(AD+AK) > KD + CD
=> 2(AD+AK) > KC (do KD+DC >KC)
0,25
0,25
0,25
0,25
0,25
5
a
Áp dụng định lí Pytago trong tam DEF vuông tại D
EF
2
= DE
2

+ DF
2
= 3
2
+
( )
2
27
= 36

EF 36
6(cm)
⇒ =
=
0,25
0,25
0,25
0,25
b
Vì I là trung điểm của EF nên:
EF 6
IE 3cm
2 2
= = =
Vì DI là đường trung tuyến ứng với cạnh huyền EF nên:
EF
DI 3(cm)
2
= =
Vậy DI = DE = IE = 3cm nên tam giác IDE là tam giác đều

0,25
0,25
* Lưu ý: học sinh có cách giải khác, đảm bảo đúng kết quả thì vẫn cho điểm tối đa.