giáo án chương 1 hàm số lượng giác

Soạn ngày17 tháng 8 năm 2015
CHƯƠNG I:

HÀM SỐ LƯỢNG GIÁC & PHƯƠNG TRÌNH LƯỢNG GIÁC
§1: Hàm số lượng giác (5 tiết)
§2: Phương trình lượng giác cơ bản(5 tiết)
§3: Một số phương trình lượng giác thường gặp(7tiết)
Ôn tập chương I (2 tiết)

A/ Mục tiêu bài dạy :
1) Kiến thức:Giới thiệu các hàm số lượng giác,sự biến thiên và đồ thị của chúng.trên cơ
sở đó trình bày các phương trình lượng giác :từ phương trình lương giác cơ bản đến các
phương trình lượng giác đơn giản có thể biến đổi để đưa về phương trình lượng giác cơ
bản.Nội dung này bao gồm phương trình bậc nhất, bậc hai đối với một hàm số lượng
giác;các phương trình có thể đưa về bậc nhất, bậc hai và phương trình bậc nhất đối với
sinx và cosx.
2) Kỹ năng : Xác định được:Tập xác định,tập giá trị,tính chẳn,lẻ, tính tuần hoàn,chu kì ,
khoảng đồng biến ,nghịch biến của các hàm số

y = sin x; y = cos x; y = tan x; y = cot x

y = sin x; y = cos x; y = tan x; y = cot x

. Vẽ

được đồ thị các hàm số
.
Giải thành thạo các phương trình lượng giác cơ bản .Biết sử dụng máy tính bỏ túi hỗ
trợ tìm nghiệm ptlg cơ bản .
Giải phương trình : bậc nhất , bậc hai đối với một hàm số lượng giác,phương trình
asinx + bcosx = c,pt có sừ dụng công thức biến đổi để giải ..

3) Tư duy- Thái độ : - Hiểu thế nào là hàm số lượng giác . phương trình lượng giác. Xây
dựng tư duy lôgíc,linh hoạt.Cẩn thận trong tính toán và trình bày.Qua bài học HS biết
được toán học có ứng dụng trong thực tiễn.
B/ Phương tiện dạy học :
1. Chuẩn bị của học sinh: xem trước bài mới
2. Chuẩn bị của giáo viên:. bài giảng, SGK, STK ,Bảng phụ. Phiếu trả lời câu hỏi
C/ Tiến trình Bài học và các hoạt động :

§1: Hàm số lượng giác (tiết 1 )
I/ Ổn định lớp : Kiểm tra sĩ số ,tình hình chuẩn bị Bài của học sinh
II/Kiểm tra Bài cũ:
Hoạt động 1 : Kiểm tra Bài cũ
Hoạt động của GV –HS
Nội dung
-Ôn tập kiến thức cũ giá trị lg -Ln bảng trả lời
của cung góc đặc Bài ệt
-Tất cả cc HS cịn lại trả lời vo
-HĐ1 (sgk) ?
vở nhp
a) Y/c HS sử dụng máy tính -Nhận xt
( lưu ý máy ở chế độ rad )
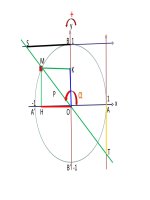
b) Sử dụng đường trịn lg Bài ểu
diễn cung AM thoả đề bài
III/ Dạy học Bài mới:


1/Đặt vấn đề chuyển tiếp vào bài mới:Ta đã học được các CTLG ,vậy lượng giác là
gì?.Lượng giác cũng là một hàm số .Vậy thì hôm nay chúng ta đi vào bài mới để khảo sát
và vẽ đồ thị của hàm số lượng giác.
2/Dạy v học Bài mới:

Hoạt động 2 : Hàm số sin và cơsin
-Đặt mỗi số thực x tương ứng -Sử dụng đường trịn lg thiết I. Các định nghĩa :
điểm M trên đường tròn lượng lập .
1. Hàm số sin và cơsin :
giác m sđ cung lg AM bằng x . -Có duy nhất điểm M có tung
a) Hàm số sin : (sgk)
Nhận xét số điểm M . Xác định độ là sinx, hoành độ điểm M là
giá trị sinx, cosx tương ứng
cosx,
sin : R→R
x a y = sin x
-Nhận xt, ghi nhận
-Sửa chữa, uốn nắn cách biểu
đạt của HS?
Tập xác định là R
-Định nghĩa hàm số sin như sgk
[ −1;1]
-Tập xác định,tập giá trị của -Suy nghĩ trả lời
y = sin x
Tập giá trị
-Nhận xét
hàm số
-Ghi nhận kiến thức
Hoạt động 3 : Hm số cơsin
-Xây dựng như hàm số sin ?
-Xem sgk , trả lời
b) Hàm số côsin : (sgk)
-Phátbiểu định nghĩa hàm số -Nhận xét
cos : R→R
x a y = sin x

côsin
-Tập xác định,tập giá trị của hàm -Ghi nhận kiến thức
y = cos x
Tập xác định là R
số
[ −1;1]
y = sin x
Tập giá trị là
-Củng cố hàm số
,
y = cos x

Hoạt động 4 : Hàm số tang và cơtang
-Định nghĩa như sgk
-HS trả lời
-Tập xác định?
-Nhận xt

2. Hàm số tang và cơtang :
a) Hàm số tang : (sgk)
y=

-Ghi nhận kiến thức

Ký hiệu :

TXĐ:
Hoạt động 5 : Hàm số côtang
-Định nghĩa như sgk
-Trả lời

-Tập xác định?
-Nhận xt
-HĐ2 sgk ?

sin x
cos x

( cos x ≠ 0)

y = tan x

π

D = ¡ \  + kπ , k ∈ ¢ 
2


b) Hm số cotang : (sgk)


-Thế nào là hàm số chẳn, -Ghi nhận kiến thức
lẻ ?
-Chỉnh sửa hòan thiện
sin(-x) = - sinx
cos(-x) = cosx

y=

cos x
sin x

(sin x ≠ 0)

y = cot x

Ký hiệu :
TXĐ: D =R\{k, k}
Nhận xt : sgk

§1: Hàm số lượng giác (tiết 2 )
Hoạt động của GV –HS

Nội dung

-HĐ3 sgk ?

II. Tính tuần hoàn của
hàm số lượng giác (sgk)

-Xem sgk, trả lời
-Nhận xét
-Ghi nhận kiến thức

-Chỉnh sửa hoàn thiện

Hàm

số

y = sin x; y = cos x

tuần hoàn với chu kỳ
H

2π

y = ta n x; y = cot x

hoàn với chu kỳ

π

tuần

Hoạt động 3 ( Củng cố, luyện tập )
a) Hàm số f( x ) = cos5x có phải là hàm số chẵn không ? Vì sao ?
π
7
b) Hàm số g( x ) = tg( x + ) có phải là hàm số lẻ không ? Vì sao ?
a)Tập xác định của f( x ) là - Củng cố khái niệm về hàm
∀x ∈ R có tính chất đối lượng giác: Định nghĩa, tập
xác định, tập giá trị, tính
xứng, và:
f( - x ) = cos( - 5x ) = chẵn lẻ, tuần hoàn và chu kì
cos5x nn f( x ) là hàm số -ôn tập về công thức góc có
liên quan đặc biệt( góc đối ),
chẵn
Tập xác định của g( x ) là định nghĩa hàm chẵn lẻ
∀x ∈ R có tính chất đối - Nêu các mục tiêu cần đạt
của bài học

xứng, và:

b)g( - x ) = tg( - x +

tg[ - ( x -

π
7

π
7

)=

) ] = - tg ( x -


π
7

π
7

) ≠ tg( x +
) nên g(x)
không phải hàm lẻ
§1: HÀM SỐ LƯỢNG GIÁC ( tiết 3)
Hoạt động 1 : Kiểm tra bài cũ
Hoạt động của GV –HS
NỘI DUNG

-Tập xác định, tập giá trị, tính -HS trả lời
chẵn, lẻ và tính tuần hoàn của -Tất cả cc HS còn lại trả lời vào
hàm số lg?
vở nháp
-Treo bảng phụ kết quả
-Nhận xét
Hoạt động 2 : Sự biến thiên và -Suy nghĩ trả lời
đồ thị của hàm số lượng giác
-Nhận xét
-Ghi nhận kiến thức
[ 0; π ]
-Xét trên đoạn
như sgk?
-Nêu sbt và đồ thị của hàm số
y = sin x

trên các đoạn
[ −2π ; −π ] ; [ 2π ;3π ] ; ¡
?
-Chỉnh sửa hoàn thiện

π

0

0

y = sin x

2. Hàm số y = cosx :

BBT
x

y = cosx

trên các đoạn
[ −π ; 0] ; [ π ; 2π ] ; ¡
?
ta

π
2

0

1

-Suy nghĩ trả lời
-Nhận xt
-Xét trên đoạn
như ?
-Nêu sbt và đồ thị của hàm số -Ghi nhận kiến thức

x∈¡

x

y = s in x

[ 0; π ]

-

III. Sự biến thiên và đồ thị của
hàm số lượng giác:
1. Hàm số y = sinx :
BBT

0
1

π
2

π

0

−1

có


π

sin  x + ÷ = cos x
2

y = sin x

tịnh tiến đồ thị
r  π 
véctơ

u =  − ;0 ÷
 2 
y = cos x

theo

được đồ thị

hàm số
Hoạt động 3 : Hàm số y = cosx


§1: HÀM SỐ LƯỢNG GIÁC (tiết 4)
Hoạt động 1 : Hàm số y = tanx
Hoạt động của GV
Hoạt động của HS
-Xét trên nữa khoảng -Suy nghĩ trả lời
-Nhận xét
 π
0; 2 ÷
-Ghi nhận kiến thức
?
-Sử dụng tính chất hàm số
lẻ được đồ thị trên khoảng
 π π

NỘI DUNG
3. Hàm số y = tanx :
BBT
x

0

y =

π
2
+∞

tg x

0

 − 2 ; 2 ÷

-Suy ra đồ thị hàm sồ trên D
-Chỉnh sửa hoàn thiện

Hoạt động 2 : Hàm số y = cotx
-Xét trên nữa khoảng -Suy nghĩ trả lời
-Nhận xét
 π
0; 2 ÷
-Ghi nhận kiến thức
?
-Sử dụng tính chất hàm số

lẻ được đồ thị trên khoảng
 π π
 − 2 ; 2 ÷


-Suy ra đồ thị hàm sồ trên
D
-Chỉnh sửa hoàn thiện

4. Hàm số y = cotx : tương tự
BBT
x

π
0
+∞

2

y = c o tg x

0


BÀI TẬP HÀM SỐ LƯỢNG GIÁC (tiết 5)
Hoạt động 1 : Kiểm tra Bài cũ
Hoạt động của GV –HS
NỘI DUNG
-Ôn tập kiến thức cũ giá trị lg -HS trình bày bài làm
1) BT1/sgk/17 :

của cung góc đặc Bài ệt
-Tất cả các HS còn lại trả
x ∈ { −π ;0; π }
-BT1/sgk/17 ?
lời vào vở nháp
a)
-Căn cứ đồ thị y = tanx trên -Nhận xét
 3π π 5π 
x ∈ − ; ; 
-Chỉnh sửa hoàn thiện nếu
3π 

 4 4 4 
 −π ; 2 
có
b)
-Ghi nhận kết quả
đoạn
π   π   3π 

x ∈  −π ; − ÷U  0; ÷U  π ; ÷
2
2
2
c)
b)



 

 



 π  π 
x ∈  − ;0 ÷U  ; π ÷
 2  2 

Hoạt động 2 : BT2/SGK/17
-BT2/sgk/17 ?
-Xem BT2/sgk/17
2) BT2/sgk/17 :
sin x ≠ 0
-HS trình bày bài làm
D = ¡ \ { kπ , k ∈ ¢}
-Điều kiện :
-Tất cả các HS còn lại trả lời a)
-Điều kiện : 1 – cosx > 0 hay vào vở nháp
D = ¡ \ { k 2π , k ∈ ¢}
cos x ≠ 1
-Nhận xét
b)
-Chỉnh
sửa
hoàn
thiện
nếu
có
π π

 5π

x − ≠ + kπ , k ∈ ¢
D = ¡ \  + kπ , k ∈ ¢ 
-Ghi nhận kết quả
3

-Điều kiện :
x+

-Điều kiện :

2

π
≠ kπ , k ∈ ¢
6

c)
d)

6

 π

D = ¡ \  − + kπ , k ∈ ¢ 
 6


Hoạt động 3 : BT3/SGK/17

-BT3/sgk/17 ?
-Xem BT3/sgk/17
3) BT3/sgk/17 :
sin
x
,sin
x
≥
0
-HS
trình
bày
bài
làm
sinx

sin x = 
-Tất
cả
các
HS
còn
lại
trả
lời
Đồ thị của hàm số y =
,s in x < 0
 − sin x
vào vở nháp
-Nhận xét

s in x < 0
M
-Chỉnh sửa hoàn thiện nếu có
⇔ x ∈ ( π + k 2π , 2π + k 2π ) , k ∈ ¢
-Ghi nhận kết quả
lấy đối xứng qua Ox phần đồ thị
hs

y = sin x

trên các khoảng này




BÀI TẬP HÀM SỐ LƯỢNG GIÁC (tiết 6)
Hoạt động 1 : BT4/SGK/17
Hoạt động của GV
Hoạt động của HS
NỘI DUNG
-BT4/sgk/17 ?
-Xem BT4/sgk/17
4) BT4/sgk/17 :
y = sin 2 x
-HS trình bày bài làm
-Hàm số
lẻ tuần -Tất cả các HS còn lại trả lời sin 2 ( x + kπ ) = sin ( 2 x + 2kπ )
π
vào vở nháp
= sin 2 x

,k ∈ ¢
hòan chu kỳ
ta xét trên
-Nhận xét
 π
-Chỉnh sửa hoàn thiện nếu có
 0; 2 
-Ghi nhận kết quả
đoạn
lấy đối xứng qua O được đồ
 π π
 − 2 ; 2 

thị trên đoạn
, tịnh
tiến -> đt
Hoạt động 2 : BT5/SGK/18
-BT5/sgk/18 ?
-Xem BT5/sgk/18
5) BT5/sgk/18 :
y = cos x
-HS trình bày bài làm
-Cắt đồ thị hàm số
bởi -Tất cả cc HS còn lại trả lời vo
1
vở nhp
y=
2
-Nhận xt
đường thẳng

được giao -Chỉnh sửa hồn thiện nếu có
điểm
-Ghi nhận kết quả
±

π
+ k 2π , k ∈ ¢
3

x=
Hoạt động 3: BT6,7/SGK/18
-BT6/sgk/18 ?
-Xem BT6,7/sgk/18
6) BT6/sgk/18 :
sin x > 0
-HS trình bày bài làm
( k 2π , π + k 2π ) , k ∈ ¢
ứng phần đồ thị nằm -Tất cả các HS còn lại trả lời
trên trục Ox
vào vở nháp
7) BT7/sgk/18 :
-BT7/sgk/18 ?
-Nhận xét
cos x < 0
-Chỉnh sửa hoàn thiện nếu có
ứng phần đồ thị nằm


dưới trục Ox
-BT8/sgk/18 ?

a)
Từ

-Ghi nhận kết quả
đk

0 ≤ cos x ≤ 1 ⇒ 2 cos x ≤ 2

⇒ 2 cos x + 1 ≤ 3 hay y ≤ 3

: b)

sin x ≥ −1 ⇔ − sin x ≤ 1

3 − 2 sin x ≤ 5 hay y ≤ 5

3π
π

+ k 2π ÷, k ∈ ¢
 + k 2π ,
2
2


8) BT8/sgk/18 :

max y = 3 ⇔ cos x = 1

a)

⇔ x = k 2π , k ∈ ¢
max y = 5 ⇔ sin x = −1

b)
⇔ x=−

π
+ k 2π , k ∈ ¢
2


§2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN (tiết 7)
Hoạt động 1 : Kiểm tra Bài cũ
Hoạt động của GV –HS
NỘI DUNG
1 -Lên bảng trả lời
sin x =
2 -Tất cả các HS còn lại trả lời
-Tìm giá trị của x để
vào vở nháp
?
-Nhận xét
-Cách biểu diễn cung AM trên
đường tròn lượng giác ?
-HĐ1 sgk ?
-Ptlg cơ bản
Hoạt động 2: ( Dẫn dắt khái niệm ).Có giá trị nào của x để sinx = - 2 ?
- Dùng máy tính bỏ túi :
sin x ≤ 1

My cho kết quả Math ERROR
Giải thích: Do
nn | a | > 1 thì
( lỗi php phương trình sinx = a vơ nghiệm.
tốn)
Với | a | ≤ 1 phương trình sinx = a
- Dng mơ hình đường trịn lượng có nghiệm
giác: không có giao điểm của y = 2 với đường trịn
- Giải thích bằng t/c của hm y =
sinx
Hoạt động 3 : Hình thành công thức nghiệm
-HĐ2 sgk ?
-Xem HĐ2 sgk
1. Phương trình sinx = a : (sgk)
sin x = a
-Trình bày bài giải
-Phương trình
nhận xét -Nhận xét
 x = α + k2π
sinx = sinα ⇔ 
a?
-Chỉnh sửa hoàn thiện
 x = π − α + k2π
a >1
-Ghi nhận kiến thức
nghiệm pt ntn ?
Chú ý : (sgk)
a ≤1

sin

-

nghiệm pt ntn ?
-1≤ sinx≤1
-Minh hoạ trên đtròn lg
-Kết luận nghiệm
π
 π
− ≤ α ≤
-Nếu

2
 2
sin α = a

thì

α = arcsin a

 x = arcsin a + k2π, k ∈ ¢
 x = π − arcsin a + k2π, k ∈ ¢


a

M'

O

M
cos

Trường hợp đặc biệt
sinx = 1 ⇔ x =

π
+ k2π ( k ∈ ¢ )
2

sinx = −1 ⇔ x = −

-Trình bày bài giải , nhận
xét
-Chỉnh sửa , ghi nhận kiến
thức

π
+ k2π ( k ∈ ¢ )
2

sinx = 0 ⇔ x = kπ ( k ∈ ¢ )


-VD1 sgk ? N1,2 a) N3,4 b)
-HĐ3 sgk ?


§2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN (tiết 8)
Hoạt động của GV

Hoạt động của HS
NỘI DUNG
- Đọc, nghiên cứu SGK phần - Tổ chức theo nhóm để học
phương trình cơ bản cosx = a
sinh đọc, nghiên cứu phần
- Trả lời câu hỏi của giáo viên, phương trình cosx = a
Bài ểu đạt sự hiểu của bản thân về - Phát vấn: Điều kiện có
điều kiện có nghiệm, công thức nghiệm, công thức nghiệm,
nghiệm của phương trình cosx = a cách viết nghiệm trong
trường hợp đặc Bài ệt : a = 1; 0; 1. Kí hiệu arccos
cos x = a
-Xem sgk
2. Phương trình cosx = a
-Phương trình
nhận xét -Nhận xét
(sgk)
a?
-Chỉnh sửa hoàn thiện
a >1
-Ghi nhận kiến thức
cosx = cosα ⇔ x = ±α + k2π, k ∈
nghiệm pt ntn ?
a ≤1

-

Chú ý : (sgk)

sin

nghiệm pt ntn ?
≤ cosx ≤

M

?

-Minh hoạ trên đtròn lg
-Kết luận nghiệm
0 ≤ α ≤ π

cos α = a
α = arccos a
-Nếu
thì
x = ± arcsin a + k2π, k ∈ ¢

a
O

Trường hợp đặc Bài ệt

cosx = 1 ⇔ x = k2 π ( k ∈ ¢ )

cos

M'

cosx = −1 ⇔ x = π + k2π ( k ∈ ¢

-Trình bày bài giải
-Nhận xét
-Chỉnh sửa
-Ghi nhận kiến thức

cosx = 0 ⇔ x =

π
+ kπ ( k ∈ ¢ )
2

-Xem VD2 sgk
-HĐ4 sgk ? N1,2 a) N3,4 b)
Hoạt động 3 : Hình thành công thức nghiệm
Hoạt động 4:( Củng cố khái niệm )
π
6

−

2
2

1
3

Giải các phương trình: a) cosx = cos
b) cos3x =
c) cosx =
2

2
d) cos( x + 600) =
π
4 HS ln bảng thực hiện - Củng cố về phương trình sinx = a,
± + k2π
cos = a : Điều kiện có nghiệm, công
6
thức nghiệm, cc cơng thức thu gọn a) x =

k∈Z


π
2π
nghiệm, kí hiệu arcsin, arccos
± +k
- Các trường hợp:
4
3
b) x =
k∈Z
sinx = sinα, cosx = cosα
1
ĐVĐ: Có thể giải được các phương
3
trình khơng phải l cơ bản không ?
c) x = ± arccos + k2π k ∈ Z

d)

 x = −150 + k3600

0
0
 x = −105 + k360

k∈Z

Hoạt động 5:Thực hiện hoạt động 4 /23 SGK
Giải phương trình: 5cosx - 2sin2x = 0
HS lên bảng thực hiện - Hướng dẫn học sinh:
Đưa phương trình đưa cho về dạng:
đưa về phương trình cơ bản để viết ( 5 - 4sinx )cosx = 0
nghiệm
 cosx = 0

- Củng cố về phương trình sinx = a,
 sin x = 5
cos = a

4
⇔
⇔ cosx = 0
π
+ kπ
2
hay x =
k∈Z

§2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN (tiết 9)
A
Hoạt động 1 : Kiểm tra Bài cũ
Hoạt động của GV -HS
NỘI DUNG
-Giải phương trình :
-Lên bảng trả lời
1
-Tất cả các HS còn lại trả lời vào vở
sin x =
nháp
2
a)
b) -Nhận xét
−1
-Ghi nhận kiến thức
cos x =
2

-Chỉnh sửa hoàn thiện
Phương trình tanx = a
- Hướng dẫn học sinh viết điều kiện của
x thỏa mãn cosx ≠ 0
Do tgx = a ⇔
nên điều kiện - ĐVĐ: Viết công thức nghiệm của
của phương trình cosx ≠ 0
phương trình tanx = a ?
sin x
cosx

π
+ kπ
2

⇔x≠
Hoạt động 2:( Dẫn dắt khái niệm ).Viết điều kiện của phương trình tgx = a, a ∈ R ?
Hoạt động 3:( Dẫn dắt khái niệm ).Đọc sách giáo khoa phần phương trình tgx = a
- Đọc sách giáo khoa phần - Hàm y = tanx tuần hòan có chu kì bao
phương trình tanx = a
nhiêu ?
- Trả lời các câu hỏi của giáo - Đặt a = tanα, tìm các giá trị của x thoả
viên biểu đạt sự hiểu của mình mãn tanx = a ?
về các vấn đề đã đọc
- Giải thích kí hiệu arctana ?
- Viết và hiểu được các công - Viết công thức nghiệm của phương trình
thức
trong trường hợp x cho bằng độ
x = α + kπ và
x = arctana + kπ
x = α0 + k1800 với k ∈ Z
Hoạt động 4 : Hình thành công thức nghiệm
-Điều kiện tanx có nghĩa ?
-Xem HĐ2 sgk
1. Phương trình tanx = a : (sgk)
π
-Trình bày như sgk
-Trình bày bài giải
x ≠ + kπ ( k ∈ ¢ )
-Minh hoạ trên đồ thị
-Nhận xét

2
Điều kiện :
-Giao điểm của đường thẳng y = a -Chỉnh sửa hoàn thiện
y = tan x
-Ghi nhận kiến thức
và đồ thị hàm số
?
x = arc ta n a + kπ, k ∈ ¢
-Kết luận nghiệm
Chú ý : (sgk)


-Nếu

π
 π
− ≤ α ≤
2
 2
ta n α = a

tanx = tanα ⇔ x = α + kπ, k ∈ ¢

thì

α = arctan a

x = arc ta n a + kπ, k ∈ ¢

-VD3 sgk ?

-HĐ5 sgk ? N1,2 a) N3,4 b)

-Trình bày bài giải , nhận xét
-Chỉnh sửa , ghi nhận kiến
thức

Củng cố ,khắc sâu kiến thức : Viết các công thức nghiệm của các phương trình:
a) tgx = 1
b) tgx = 0
c) tgx = - 1
HS ln bảng thực hiện

π
- Pht vấn: Chỉ r ( có giải thích ) sự
+ kπ
tương đương của các phương trình:
4
tgx = 1, tgx = 0, tgx = - 1 với các a) tgx = 1 ⇔ x =
b) tgx = 0 ⇔ x = kπ
phương trình sinx - cosx = 0
π
sinx = 0, sinx + cosx = 0
− + kπ
4
c) tgx = - 1 ⇔ x =


§2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN (tiết 10)
Hoạt động 1 : Kiểm tra bài cũ
Gọi một học sinh ln bảng chữa Bài tập 3(a, b ) trang 25

Hoạt động 2:( Dẫn dắt khái niệm .Viết điều kiện của phương trình cotgx = a, a ∈ R ?
Hoạt động của GV
Hoạt động của HS
NỘI DUNG
cosx
- Hướng dẫn học sinh viết điều kiện
của x thỏa mn sinx ≠ 0
sin x
Do cotgx = a ⇔
nên - ĐVĐ: Viết công thức nghiệm của
điều kiện của phương trình phương trình cotgx = a ?

kπ

l sinx ≠ 0 ⇔ x ≠
Hoạt động 3:( Dẫn dắt khái niệm )Đọc sách giáo khoa phần phương trình cotgx = a
- Đọc sách giáo khoa phần phương - Hm y = cotgx tuần hồn có
trình cotgx = a
chu kì l bao nhiu ?
- Trả lời các câu hỏi của giáo viên Bài - Đặt a = cotgα, tìm cc gi trị
ểu đạt sự hiểu của mình về cc vấn đề của x thoả mn cotgx = a ?
đ đọc
- Giải thích kí hiệu arccotga
- Viết và hiểu được các công thức
?
x = α + kπ v x = arccotga + kπ - Viết cơng thức nghiệm
x = α0 + k1800
với k của phương trình trong
trường hợp x cho bằng độ
∈Z

Hoạt động 4 : Hình thành công -Xem HĐ2 sgk
1. Phương trình cotx = a :
thức nghiệm -Điều kiện cotx có -Trình bày bài giải
(sgk)
nghĩa ?
-Nhận xét
x ≠ kπ ( k ∈ ¢ )
-Trình bày như sgk
-Chỉnh sửa hoàn thiện
Điều kiện :
-Minh hoạ trên đồ thị
-Giao điểm của đường thẳng y =
x = arc cota + kπ, k ∈ ¢
y = tan x

a và đồ thị hàm số
?
-Kết luận nghiệm
0 ≤ α ≤ π

cotα = a
α = arc co t a
-Nếu
thì

Chú ý : (sgk)
-Ghi nhận kiến thức
-Trình bày bài giải , nhận xét
-Chỉnh sửa , ghi nhận kiến thức

cotx = cotα ⇔ x = α + kπ, k ∈ ¢

x = arc cota + kπ, k ∈ ¢

-VD4 sgk ?
-HĐ6 sgk ? N1,2 a) N3,4 b)

Ghi nhớ : (sgk)
Củng cố ,khắc su kiến thức : Viết các công thức nghiệm của các phương trình sau:


1
3

2π
7

a) cotg4x = cotg
b) cotg3x = - 2
c) cotg( 2x - 10 0) =
HS lên bảng thực - Hướng dẫn học sinh viết
2π
2π
hiện
các công thức nghiệm
7
7
- Uốn nắn cách biểu đạt, a) cotg4x = cotg
⇔ 4x =
+ kπ

trình bày bài giải của học
π
π
sinh

14

b) cotg3x = - 2

⇔x =

c) cotg( 2x - 100) =
V/Hướng dẫn học tập ở nhà : Xem bài và BT đ giải
Bài tập về nh:5,7 ( Trang 29 - SGK )

4

⇔x =
+k
k∈Z
⇔ 3x = arccotg(- 2 ) + kπ

1
3

1
3

arccotg(- 2 ) + k

π
3

⇔ 2x - 100 = 600 + k1800
⇔ x = 350 + k900 k ∈ Z


LUYỆN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN (tiết 11)
Hoạt động 1
Hoạt động của GV
Hoạt động của HS
NỘI DUNG
-Ôn tập kiến thức cũ giá trị lg của -HS trình bày bài làm
1) BT1/sgk/17 :
1
cung góc đặc biệt
-Tất cả các HS còn lại

x = arcsin − 2 + k 2π

-BT1/sgk/28 ?
trả lời vào vở nháp
3
(k ∈ ¢ )

-Căn cứ công thức nghiệm để giải
-Nhận xét
 x = π − arcsin 1 − 2 + k 2π

-Chỉnh sửa hoàn thiện

 x = −400 + k .1800
3
(
k
∈
¢
)

nếu
có
a)
0
0
 x = 110 + k .180
π
2π
-Ghi nhận kết quả
x= +k
(k ∈ ¢ )
d)
6

b)
x=

c)

3

π

3π
+k
(k ∈ ¢ )
2
2

Hoạt động 2 : BT2/SGK/28
-BT2/sgk/28 ?
-Xem BT2/sgk/28
2) BT2/sgk/28 :
sin3x = sin x
-HS trình bày bài làm
3x = x + k 2π
-Giải pt :
-Tất cả các HS còn lại trả lời 3x = π − x + k 2π
-Chỉnh sửa hoàn thiện nếu có
vào vở nháp
 x = kπ
-Nhận xét
⇔
(k ∈ ¢ )
-Ghi nhận kết quả
x = π + k π


Hoạt động 3 : BT3/SGK/28
-BT3/sgk/28 ?
-Xem BT3/sgk/28
-Căn cứ công thức nghiệm để -HS trình bày bài làm
giải

-Tất cả trả lời vào vở nháp
-Nhận xét
-Chỉnh sửa hoàn thiện nếu có
π

x
=
±
+
k
π

-Ghi
nhận
kết
quả
6
(k ∈ ¢ )

2
 x = ± π + kπ
x = 1 ± arccos + k 2π (k ∈ ¢ )
3


3

d)
Củng cố ,khắc su kiến thức :
1 / cos( x + 2) =

Giải một số phương trình lượng giác sau:

2
5

4

2

3) BT3/sgk/28 :
b)
a)
c)

x = ±40 + k1200 ( k ∈ ¢ )
11π
4π

 x = 18 + k 3
(k ∈ ¢ )

 x = − 5π + k 4π

18
3

2 / 2 cos( x + 70 0 ) = 2

§2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN (tiết 12)
Hoạt động 1 : BT4/SGK/29
Hoạt động của GV -HS
NỘI DUNG
-BT4/sgk/29 ?
-Xem BT4/sgk/29
4) BT4/sgk/29 :
-Tìm điều kiện rồi giải ?
-HS trình bày bài làm
π
π


2 x = + k 2π
x = + kπ

s ìnx ≠ 1
-Tất cả các HS còn lại trả lời 
2
4
⇔
(k ∈ ¢ )

-Điều kiện :
vào vở nháp
π
π


2 x = − + k 2π

x = − + kπ
cos 2 x = 0
-Nhận xét


2
4
-Giải pt :
-Chỉnh sửa hoàn thiện nếu có
-KL nghiệm ?
π
-Ghi nhận kết quả
x = − + kπ ( k ∈ ¢ )
π
4
x = + kπ
4
Nghiệm của pt là
Loại
do điều kiện
Hoạt động 2 : BT5/SGK/29
-BT5/sgk/29 ?
-Xem BT5/sgk/29
5) BT5/sgk/29 :
-Căn cứ công thức nghiệm để -HS trình bày bài làm
x = 450 + k1800 (k ∈ ¢ )
giải
-Tất cả các HS còn lại trả lời vào a)
-Điều kiện c) và d) ?
vở nháp

1 5π kπ
x= +
+
(k ∈ ¢ )
ĐS:
-Nhận xét
3 18 3
b)
-Chỉnh sửa hoàn thiện nếu có
π

 x = 2 + kπ
π kπ
-Ghi nhận kết quả

x= +
(k ≠ 3m, m ∈ ¢ )


cos
x
≠
0
sin
x
≠
0
4 2 (k ∈ ¢ )
x = k π


c)
:
;
d)
:

 x = kπ
3
c)
Hoạt động 3 : BT6,7/SGK/29
-BT6/sgk/29 ?
-Xem BT6,7/sgk/29
6) BT6/sgk/29 :
-Tìm điều kiện ?
-HS trình bày bài làm
π

cos 2 x ≠ 0, cos  − x ÷ ≠ 0
-Tất cả trả lời vào vở nháp, ghi
π

4

tan  − x ÷ = t an 2 x
nhận
ĐK
:
4



cos 3 x ≠ 0, cos x ≠ 0
-Giải pt :
?
7) BT7/sgk/29 :
b)
ĐK
:
π
π

⇒ 2 x = − x + kπ
cos 5 x = cos  − 3 x ÷
1
4
π
π
⇒ x = + k ( k ≠ 3m − 1, m ∈ ¢ )
12
3

-BT7/sgk/18 ?
-Đưa về pt cos ?
-Tìm điều kiện 7b) ?
-Nhận xét
-Chỉnh sửa hoàn thiện nếu có

⇒ tan 3x =

⇒ tan 3 x = cot x
tan x

π

⇒ tan 3x = tan  − x ÷
2

π
⇒ 3 x = − x + kπ
2
π
π
⇒ x = + k (k ∈ ¢ )
8
4

IV/Củng cố ,khắc su kiến thức:Đ củng cố từng phần

a)

2



π

⇔ 5 x = ±  − 3x ÷+ k 2π , k ∈ ¢
2

π
π


 x = 16 + k 4
⇔
( k ∈¢)
 x = − π + kπ

4


V/Hướng dẫn học tập ở nhà : Xem bài và BT đã giải
Xem trước bài “ MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC
THƯỜNG GẶP “


GIẢI CÁC PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
BẰNG MÁY TÍNH BỎ TÚI (Tiết 13)
Hoạt động 1 ( Dẫn dắt khi niệm )
Hoạt động của GV -HS
NỘI DUNG
- Chia nhóm để nghiên cứu sách - Hướng dẫn học sinh dùng máy Dùng máy tính bỏ túi fx giáo khoa phần hướng dẫn sử tính bỏ túi: fx - 500MS hoặc máy 500MS, giải các phương trình:
dụng máy tính fx - 500MS giải fx - 570, fx - 500A để giải các
1
các phương trình đ cho
phương trình đ cho.
2
- Trả lời câu hỏi của giáo viên,
a) sinx =
b) cosx = Bài ểu đạt sự hiểu của cá nhân
1

3

c) tgx =

3

Hoạt động 2( Củng cố khi niệm )

- Ta có cotg( x + 30 0) =
nn:

1
tg(x + 300 )

=

3

1
3

tg( x + 300) =
do đó quy trình ấn phím
để giải bài toán đ cho như sau: ( Đưa máy
về chế độ tính bằng đơn vị độ )
+ Trước hết tính x + 300:

- ĐVĐ: Trong máy tính
không có nút cotg- 1 phải
dùng cách bấm phím nào để
giải được phương trình đ

cho ?
- Hướng dẫn: Do tgx.cotgx =
1 nên có thể sử dụng nt tg- 1

Dùng máy tính bỏ túi fx 500MS, giải các phương
trình:
cotg( x + 300) =

3

shift tg- 1 ( 1 ÷
3 ) = cho
0
30
+ Tính x: Ta có x + 300 = 300 + k1800 nn:
x = k1800
Củng cố ,khắc sâu kiến thức :Dùng MTBT để giải một số phương trình lượng giác sau:
sin x = −

a)

1
2

cos x = −

b)

3
2

c) tgx =

3
3

§3: MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP (Tiết 14)
Hoạt động 1 : Kiểm tra bài cũ
Hoạt động của GV –HS
NỘI DUNG


cos x =

-Giải phương trình :
sin x =

2
3

x
2
1
sin =
2
2
2

;

-Lên bảng trả lời
-Tất cả các HS còn lại trả lời
; vào vở nháp
-Nhận xét
-Chỉnh sửa hoàn thiện
-Ghi nhận kiến thức

Hoạt động 2 : Định nghĩa
-ĐN pt bậc hai ? đn pt bậc nhất -ĐN , nhận xét, ghi nhận
đv hslg ?
-Nêu ví dụ
2sin 2 x + 3sin x − 2 = 0

-Cho vd ?

3cot 2 x − 5cot x − 7 = 0

-HĐ2 sgk ?
-Chỉnh sửa hoàn thiện

-HĐ 2 sgk
-Trình bày bài giải
-Nhận xét
-Chỉnh sửa hoàn thiện
-Ghi nhận kiến thức

I.Phương trình bậc nhất đối với
một hàm số lượng giác.
1)Định nghĩa: Phương trình bậc
nhất đối với một hàm số lượng

giác là phương trình có dạng: at
+ b = 0 (1)
với a, b: hằng số, (a ≠0), t là một
trong các hàm số lượng giác.
Ví dụ:
a)2sinx – 5 =0 phương trình bậc
nhất đối với sinx;

3

b)
cotx +1 =0 phương trình bậ
nhất đối với cotx.

Hoạt động 3 : Cách giải
-Cách giải ?
-ĐK ?
-VD5 sgk ?
x
2
=
2
2
π

 x = 2 + k 4π , k ∈ ¢
⇔
 x = 3π + k 4π , k ∈ ¢

2

sin

-Nghe, suy nghĩ
-Trả lời
-Ghi nhận kiến thức
-Đọc VD5 sgk
-Trình bày bài giải
-Nhận xét
-Chỉnh sửa hoàn thiện
-Ghi nhận kiến thức

2. Cách giải : SGK
VD: Giải các PT:
a, 2 cos(3x) – 1 = 0
b, 3 tan (2x-4) + 3 = 0
c, 5 - 3 sin (x+ 7) = 0
HD
a, cos(3x) = 1/2
π
2π

x
=
+
k

9
3
⇔

 x = 8π + k 2 π

9
3
b, tan (2x-4) = -1
π
π
⇔ x = 2− +k
8
2
c, sin (x+ 7) = 5/3 .Vô nghiệm

Hoạt động 4 : Phương trình đưa về bậc nhất đối với một hàm số lượng giác
3. Phương trình đưa về phương trình bậc
-HĐ3 sgk ?
-Xem sgk, trả lời
nhất đối với một hàm số lượng giác
-Các công thức lg ?
-Nhận xét
Ví dụ:
a, 4cosx - sin2x = 0


-Ghi nhận

 cos x = 0

sin x = 2

-VD6 sgk ?

-VD7 sgk ?
-VD8 sgk ?

-Trình bày bài giải
-Nhận xét
-Chỉnh sửa hoàn thiện
-Ghi nhận kiến thức

⇔ cosx(4 - 2sinx) = 0⇔
π
x = + kπ , k ∈ ¢
2
 cosx = 0 ⇔
 sinx = 2 vô nghiệm(Vì 2 >1 )
Vậy phương trình đã cho có nghiệm là :
π
x = + kπ , k ∈ Z
2
b, 8sinxcosxcos2x = - 1
−

2sin4x = - 1 ⇔ sin4x =
π
π
π


 4 x = − 6 + k 2π
 x = − 24 + k 2
⇔


 4 x = 7π + k 2π
 x = 7π + k π


6
24
2

Củng cố ,khắc sâu kiến thức: Nội dung cơ bản đã được học ? Giải phương trình :
2 cos x + 1 = 0;cos 2 x − cos x = 0

1
2

⇔


§3: MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP(tiết 15)
Hoạt động 1 : Kiểm tra bài cũ
Hoạt động của GV
Hoạt động của HS
NỘI DUNG
-Sử dụng công thức cộng cm : -Lên bảng trả lời
-Tất cả các HS còn lại trả lời
π

sin x + cos x = 2 cos  x − ÷
vào vở nháp
4


-Nhận xét
π
-Chỉnh sửa hoàn thiện

sin x − cos x = 2 sin  x − ÷
-Ghi nhận kiến thức
4

;
Hoạt động 2 : Công thức biến đổi asinx + bcosx
-Biến đổi :
-Công thức cộng
III. Phương trình bậc nhất đố
a sin x + b cos x
với sinx và cosx :
-Nhận xét
1) Công thức Biến đổi : (sgk)
= a 2 + b 2 sin ( x + α )
-Đọc sách nắm qui trình Bài a sin x + b cos x
ến đổi
a
= a 2 + b 2 sin x + α
cos α =

với
sin α =

a +b
2

(

2

-Chỉnh sửa hoàn thiện
-Ghi nhận kiến thức

b

cos α =

với

a 2 + b2

a +b
2

sin α =

2

-Giải thích sự xuất hiện
-Sử dụng công thức cộng biến đổi
Hoạt động 3 : Phương trình dạng asinx + bcosx = c
-Xét
phương
trình
: -Nghe, suy nghĩ

a sin x + b cos x = c
-Trả lời
2
2
-Ghi nhận kiến thức
( a + b ≠ 0)
-Có thề đưa về ptlgcb ?
-VD9 sgk ?
-Ta có :

π

sin x + 3 cos x = 2sin  x + ÷
3

sin x + 3 cos x = 1

π

⇔ 2sin  x + ÷ = 1
3


-Đọc VD9 sgk
-Trình bày bài giải
-Nhận xét
-Chỉnh sửa hoàn thiện
-Ghi nhận kiến thức

2)

)

a
a + b2
2

b
a + b2
2

Phương

asinx + bcosx = c

trình

dạng

: (sgk)

-VD9 sgk ?
π
π

⇔ sin  x + ÷ = sin
3
6

π


 x = − 6 + k 2π
⇔
( k ∈ ¢)
 x = π + k 2π

2
Bài tập: Giải các phương trình sau:


2

a)
sinx – sin2x = 0;
b)8sinx.cosx.cos2x = 1.
a)
⇔

2

sinx – sin2x = 0

2

sinx(
-2cosx) = 0
s inx = 0
⇔
 cosx = 2


2
• s inx = 0 ⇔ x = k π, k ∈ Z

π

x = + k 2π

2
4
•cosx =
⇔
2
 x = − π + k 2π

4
Vậy …
b)8sinx.cosx.cos2x = 1
⇔ 4 sin 2 x.cos2x = 1
⇔ 2 sin 4 x = 1
⇔ sin 4 x =

1
2

π

4
x
=
+ k 2π


6
⇔
 4 x = π − π + k 2π

6
Vậy …

Củng cố ,khắc su kiến thức: Nội dung cơ bản đã được học ?
Giải phương trình:
2

3tan x - 2

3

2

2

a) cos x - 3cosx + 2 = 0 b) 2sin x +

2

sinx - 2 = 0

tanx - 3 = 0

BÀI 3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP (Tiết 17)
3

Hoạt đông 1/ Kiểm tra bài cũ:
Giải phương trình : 2 sin (x-1 ) = 0 và 3
cos (x-5) + 9 = 0 .
Hoạt động của GV & HS
Nội dung
HĐ2.Giải phương trình bậc hai đối với 1 HSLG.

c)