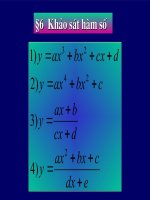Khảo sát hàm bậc ba giải tích 12 ( Hội Giảng )

1. Nêu sơ đồ khảo sát hàm số.

I. SƠ ĐỒ KHẢO SÁT HÀM SỐ
1. Tìm tập xác định
2. Sự biến thiên của hàm số
a. Chiều biến thiên của hàm số
Xét tính chẵn lẻ và tuần hoàn của hàm số (nếu có)
- Tính đạo hàm của hàm số,
- Tìm các điểm tới hạn

b. Tính các cực trị
c. Tính các giới hạn của hàm số
* Khi x dần tới vô cực
* Khi x dần tới, bên trái và bên phải, các giá trị của x tại đó hàm số
không xác định
* Tìm các tiệm cận (nếu có)
e. Lập bảng biến thiên ( ghi tất cả các kết quả tìm được
vào bảng biến thiên)
d. Xét tính lồi, lõm và tìm điểm uốn của đồ thị hàm số
(đối với các hàm số trong chương trình)
* Tính đạo hàm cấp hai
* Xét dấu đạo hàm cấp 2
* Suy ra tính lồi, lõm và điểm uốn của đồ thị

3. Vẽ đồ thị
* Chính xác hoá đồ thị
* Vẽ đồ thị
2. MỘT SỐ HÀM SỐ ĐA THỨC
1. Hàm số
3 2

axy bx cx d= + + +

Ví dụ 2: Khảo sát và vẽ đồ thị của hàm số
3
3 2y x x= − + +
Ví dụ 1: Khảo sát và vẽ đồ thị của hàm số
3 2
3 9 5y x x x= − − −

1. Tâp xác định: R
2. Chiều biến thiên
a. Sự biến thiên
2
' 3 3y x= − +
2
' 0 1 0y x= ⇔ − =
" 6 ; " 0 0y x y x= − = ⇔ = ⇒
* Đạo hàm
b. Cực trị: Hàm số đạt cực đại tại
điểm x=1 và giá trị cực đại bằng 4.
Hàm số đạt cực tiểu tại x=-1, giá
trị cực tiểu bằng 0
d. Tính lồi lõm, điểm uốn
Điểm uốn
(0; 2)
U
c) Giới hạn :
3
3
lim lim( ) ;

lim lim ( )
x x
x x
y x
y x
→∞ →∞
→−∞ →−∞
= − = −∞
= − = +∞
x=1 hoặc x= -1
Hàm số đồng biến trên khoảng (-1;1);
nghịch biến trên các khoảng và
( ; 1)−∞ −
(1; )+∞
3. Đồ thị
Điểm cắt trục tung: (0;2)
Điểm cắt trục hoành: (-1,0) và (2,0)
0
x
y