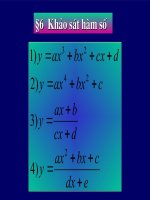tiet 13 khao sat ham bac 3

TiÕt 13


I.Sơ đồ khảo sát hàm số
I.Sơ đồ khảo sát hàm số



1
1
. Tìm TXĐ của hàm số
. Tìm TXĐ của hàm số

2. Sự biến thiên của hàm số
2. Sự biến thiên của hàm số



a, Xét chiều biến thiên của hàm số
a, Xét chiều biến thiên của hàm số



* Tính đạo hàm y' ;
* Tính đạo hàm y' ;



* Tìm các điểm tại đó đạo hàm bằng 0 hoặc không xác định ;
* Tìm các điểm tại đó đạo hàm bằng 0 hoặc không xác định ;

* Xét dấu của đạo hàm y' và suy ra chiều biến thiên của hs ;
* Xét dấu của đạo hàm y' và suy ra chiều biến thiên của hs ;



b, Tính các cực trị
b, Tính các cực trị



c, Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận
c, Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận



( nếu có) của hàm số ;
( nếu có) của hàm số ;


d, Lập bảng biến thiên (
d, Lập bảng biến thiên (
ghi tất cả các kết quả đã tìm được vào
ghi tất cả các kết quả đã tìm được vào


bảng biến thiên)
bảng biến thiên)

3 . Vẽ đồ thị
3 . Vẽ đồ thị


* Giao với các trục toạ độ
* Giao với các trục toạ độ


* Các điểm đặc biệt (điểm cực trị , điểm uốn ...)
* Các điểm đặc biệt (điểm cực trị , điểm uốn ...)


* Chính xác hoá đồ thị
* Chính xác hoá đồ thị



Chú ý:
Chú ý:
1. Nếu hàm số tuần hoàn với chu kỳ T thì chỉ cần
khảo sát sự biến thiên và vẽ đồ thị trên một chu kỳ,
sau đó tịnh tiến đồ thị song song với trục Ox
2. Nên tính thêm toạ độ một số điểm , đặc biệt là
toạ độ các giao điểm của đồ thị với các trục toạ độ
3. Nên lưu ý đến tính chẵn, lẻ của hàm số và tính
đối xứng của đồ thị để vẽ cho chính xác.

Trên khoảng (- ,-2) và ( 0, + ), y' > 0 nên hs ĐB.

Trên khoảng ( -2, 0 ), y' < 0 nên hs NB.


x-2 0
-
+
+
y
,
Ví dụ 1: Khảo sát hàm số : y = x
3
+ 3x
2
- 4
2. Sự biến thiên :
a. Chiều biến thiên : y

= 3x
2
+ 6x
y

= 0 x = 0 , x = -2
b. Cực trị : Hàm số đạt cực đại tại x = -2 ; y
cđ
= y(-2) = 0
Hàm số đạt cực tiểu tại x = 0 ; y
ct
= y(0) = -4
1. Tập xác định: D = R

c. Giới hạn
=+=+=


)
43
1()43(
32
323
xx
xLimxxLimLimy
xx
x
x
y
y
-
-2 0 +
0 0
-4
0
+
-
+ +-
d. BBT

Chú ý :
* Đồ thị hs bậc 3 có tâm đối
xứng là điểm I(-1; -2)
* Khi vẽ đồ thị nên

theo thứ tự sau :
1 - Vẽ hệ trục
2- Vẽ CĐ ,CT
3 - Vẽ đồ thị
y
x
-2 -1
0 1
-2
-4
-3
3. Vẽ đồ thị
Giao với trục oy x = 0 y = -4
Giao với trục ox y = 0 x = -3 , x = 1

B¶ng tãm t¾t ®å thÞ hµm sè bËc 3
B¶ng tãm t¾t ®å thÞ hµm sè bËc 3
a>0 a<0
y' = 0 cã
2n
0
pb
y'

= 0 cã
n
0
kÐp
y'= 0 vn

CH1 : Số cực đại , cực tiểu của hs bậc 3 phụ thuộc vào yếu tố nào?
(Phụ thuộc vào số nghiệm đơn của pt y
,
= 0)
(Luôn luôn có điểm uốn . Đồ thị có tâm đối xứng chính là
điểm uốn)
CH2 : Đồ thị của hs bậc 3 có đặc điểm gì ?
Bài tập về nhà : Bài số 1. Trang 23 (SGK)
Bài học của chúng ta tạm dừng ở đây .Thân ái chào tạm
biệt các em.
Củng cố bài

Hàm số nghịch biến trên khoảng (-;-1) (-1; +)
Bài giải:
1)Tập xác định:
D = R \ {-1}
2)Sự biến thiên:
a)Chiều biến thiên
y =
(-1)(x+1)-(-x+2)
(x+1)
2
=
-x-1+x-2
(x+1)
2
=
-3
(x+1)
2

< 0 x -1
Đ6
Đ6
Khảo sát hàm số
Khảo sát hàm số
Ví dụ 1: Khảo sát hàm số:
1
2
+
+
x
x
y =

b) Cực trị
Hàm số không có cực trị
c)Giới hạn, tiệm cận:
Ví dụ 1:Khảo sát hàm số:
1
2
+
+
x
x
y =
= -.
1x
2x
+
+

= +.
1x
2x
+
+
x = -1 là tiệm cận đứng
=-1
1x
2x
+
+
y = -1 là tiệm cận ngang
( )
lim
1x


( )
lim
1x


( )
lim
1x
+

lim
x
( )

lim
1x
+

y=
y =
y=
lim
x

e, Bảng biến thiên:
x - +
y'
y
-1
- -
Đồ thị nhận giao hai tiệm cận I(-1;-1) làm tâm đối xứng
Vẽ đồ thị :
-
+
-1
-1
3 )Đồ thị
Giao với trục o x: y = 0 x=2
Giao với trục o y: x = 0 y =2
Ví dụ 1:Khảo sát hàm số:
1
2
+
+

x
x
y =