ĐỀ THI TOÁN 2017 THPT a NGHIA HUNG

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (634.24 KB, 9 trang )

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

TRƯỜNG THPT A NGHĨA HƯNG

H
oc

01

Tổ Toán

uO
nT
hi
D

ai

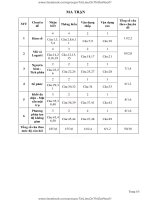
MA TRẬN TỔNG QUÁT ĐỀ THI THPT QUỐC GIA NĂM 2017 MÔN TOÁN

Mức độ kiến thức đánh giá
Nhận
biết

Thông
hiểu
4

2

Mũ và Lôgarit

4

4

3

Nguyên hàm – Tích
phân và ứng dụng

2

4

Số phức

5

Thể tích khối đa diện

6

Khối tròn xoay

7

Phương pháp tọa độ
trong không gian

2

2

11

1

1

10

4

1

0

7

3

2

1

0

6

1

2

1

0

4

1

1

1

1

4

4

2

1

1

8

Số câu

18

19

8

5

50

Tỷ lệ

36 %

38 %

16 %

10 %

s/

ro
om

.c

ok

bo

ce

.fa

Ta

iL

3

up

Hàm số và các bài toán
liên quan

Vận
dụng cao

w

w

Tổng

w

Tổng số
câu hỏi

/g

1

Vận
dụng

ie

Các chủ đề

STT

ĐỀ THI THỬ THPH QUỐC GIA MÔN TOÁN

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

y  2 x3  3x 2  1 đồng biến trên :
B) (0;1)

Câu 2: Cho hàm số

(;0)

D) R

y  x 4  4 x 2  5 . Khẳng định nào sau đây đúng?

x  2 làm điểm cực tiểu.

ai

A) Hàm số nhận

C)

uO
nT
hi
D

B) Hàm số nhận x=-5 làm điểm cực đại.
C) Hàm số nhận

x  2 làm điểm cực đại.

D) Hàm số nhận x=0 làm điểm cực đại.
Câu 3: Cho hàm số y  ax 4  bx 2  c có đồ thị như hình bên.

ie

y

A. y   x4  2 x2  3

iL

Đồ thị bên là đồ thị của hàm số nào sau đây:

m0

1
x

1

O
-1

up

và đường thẳng d: y=mx-m+2 cắt nhau tại hai điểm phân biệt khi
C) m>-1

/g

B) m>0

ro

x 1

2

s/

D. y  x 4  2 x 2  3

Câu 4: Đồ thị hàm số y  2 x

-1

Ta

B. y   x4  2 x 2

C. y  x4  2 x 2

A)

01

A) [-1;1]

H
oc

Câu 1: Hàm số

D)

0m2

om

Câu 5: Đường cong hình bên là đồ thị của hàm số y=f(x). Khẳng định nào sau đây đúng?

B) Hàm số có giá trị cực đại bằng 0
y

ok

.c

A) Đồ thị hàm số có 3 điểm cực trị

3
2

ce

bo

1
x
-3

-1

1
-1
-2

D)Hàm số đạt cực tiểu tại x=2

w

w

.fa

C) Hàm số có giá trị lớn nhất là 2

w

-2

Câu 6: Số điểm cực trị của đồ thị hàm số

y  e x ( x 2  3x  5) là

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

-3

2

3

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

A) 2

B) 0

C) 1

D)3

uO
nT
hi
D

ai

H
oc

01

Câu 7: . Cho hàm số y  f ( x) có bảng biến thiên như sau. Tìm khẳng định sai

A) Hàm số đồng biến trên khoảng (0;1)
B) Hàm số đạt một cực đại tại x=1.

ie

C) Phương trình f(x)= m có đúng 2 nghiệm thực khi m<2

iL

D) Đồ thị hàm số có tiệm cận đứng x=0





up

2



2

ro

y





/g

x
y'



om

2

B)2

C)3

D)4

.c

A)1

s/

Ta

câu 8 Cho hàm số y  f  x  có bảng biến thiên sau. Hỏi đồ thị hàm số đó có mấy tiệm cận

m 1

B)

m0

ce

A)

bo

ok

Câu 9: Tìm m để hàm số y  m  sinx nghịch biến trên khoảng (0;  )

cos 2 x
6
C)

m

5
4

D)

w

.fa

Câu 10: Đồ thị hàm số nào sau đây có đúng 2 tiệm cận ngang?
x2  x
x 2

2
B) y  4  x
x 1

C) y  x  2
x 1

D) y 

x2
x 2

w

w

A) y 

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

m2

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

500 3 . ỏy h l hỡnh ch nht cú chiu di gp ụi chiu rng, giỏ thuờ cụng nhõn xõy h l
m
3
2

B)75 triu ng

C)76 triu ng

D)77 triu ng

ab
2(log2 a log2 b)
3
ab
C) 4 log2

log2 a log2 b
3

uO
nT
hi
D

Cõu 12: Gi s ta cú h thc a 2 b2 2ab (a,b>0) H thc no sau õy ỳng

B) 2 log2 a b log2 a log2 b

A) 2 log2

D) 2 log2

ab
log2 a log2 b
2

Cõu 13:Khng nh no sau õy ỳng?

Ta

iL

ie

A) a x y a x a y ( x, y R, a 0)
B) log a ( x y) log a x log a y (0 a 1, x, y 0)

s/

C) log a x n n log a x (0 a 1, x 0)

ro

up

D) log a b log a c.logc b (0 a, b, c 1)
5

B.

a7 . a
3
a

4

C. a5 . a

om

3

a.5 a

/g

Cõu 14 : Kt qu a 2 a 0 l biu thc rỳt gn ca phộp tớnh no sau õy?
A.

D.

a5
a

ok

.c

Câu15: Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
B. y = x

bo

A. y = x -4

ce

Cõu 16. Bt phng trỡnh

.fa

A. (-; -2)

w

w

Cõu 17: Ph-ơng trình

w

A. x =

3
4

3
4

2 x 16
2

B. (1; +)

C. y = x 4

D. y =

3

x

cú tp nghim l :
C. (-; -2) (2; +)

D. (-2; 2)

43x2 16 có nghiệm là:
B. x =

4
3

C. 3

ai

A)74 triu ng

H
oc

500000 ng trờn 1 m . Hóy xỏc nh kớch thc ca h sao cho chi phớ thuờ cụng nhõn thp nht.
Chi phớ ú l

D. 5

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

01

Cõu 11: Ngi ta cn xõy mt h cha nc vi dng khi hp ch nht khụng cn np, cú th tớch l

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

C©u18: BÊt ph-¬ng tr×nh: log4  x  7   log2  x  1 cã tËp nghiÖm lµ:
B.  5; 

C. (-1; 2)

D. (-; 1)

01

A. 1;4 

m2

B.

C.

m 1

D. m  3

ai

m4

A.

B. 9ln 3

25ln 5

C.

8ln 2

uO
nT
hi
D

C©u 20 : Hàm số f ( x)  x 2 ln x có giá trị nhỏ nhất trên đoạn 3;5 là
A.

H
oc

Phương trình 4x  m.2x1  2m  0 có hai nghiệm x1 , x2 thỏa x1  x2  3 khi

C©u 19:

D. 32ln 2

C) 33 tháng

Câu 22: Tìm họ nguyên hàm của hàm số f ( x)  e

e2 x  C

2x
B) e  C

C)



om

I   eu du

.c

B)

1

bo

ok

2
Câu 24: (e2 x  3 )dx  e  a ln 2  b .
0
x 1
2

C)

B)1

w

.fa

Câu 25 Cho hàm f(x) liên t ục trên [0;10] thỏa mãn

w

I

C)0
10

10

0

6

D)

I   ueu du



D)-3
6

f ( x)dx  7 ,  f ( x)dx  3 .

0

2

1 u
e du
3

Trong đó a, b hữu tỷ. Giá trị a.b là

ce

A)3

w

2e x  C

ro

3

A) I  3 eu du

A)1

D)

I   x 2e x dx . Đặt u  x3 khi đó viết I theo u và du ta được

/g

Câu 23:

2e2 x  C

up

2

2x

s/

A)

D)100 tháng

iL

B) 81 tháng

Ta

A) 924 tháng

ie

Câu21 Một người muốn tiết kiệm tiền để mua cho mình một chiếc ô tô nên đầu mỗi tháng gửi vào

ngân hàng 4 triệu VNĐ với lãi xuất 6% năm. Hỏi sau bao nhiêu tháng người đó có thể mua chiếc ô tô
có giá 400 triệu VNĐ?

2

Khi đó P  f ( x)dx  f ( x)dx là


B) 4

C)3

D)2

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

b

Câu 26 Cho f(x) là hàm số liên tục trên [a;b] thỏa mãn

 f ( x)dx  7 .

01

a
b

H
oc

Tính I  f (a  b  x)dx bằng

a

B) a+b-7

D) a+b+7

y  x 2  1 và đường thẳng d: y=mx+2. Tìm m để diện tích hình phẳng giới hạn bởi

uO
nT
hi
D

Câu 27: Cho (P)

C) 7-a-b

(P) và d đạt nhỏ nhất

1
2

B) m=

3

4

C) m=1

D)m=0

ie

A)m=

ai

A)7

B)2ln11+6

C) 3ln11-6

D) 3ln6+6

s/

A)3ln11+6

Ta

iL

Câu 28: Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc a(t )  3 (m / s2 ) . Vận tốc ban đầu
t 1

của vật là 6 (m/s). Hỏi vận tốc của vật sau 10s là bao nhiêu?

up

Câu 29 Cho số phức z = a + bi. Tìm mệnh đề đúng trong các mệnh đề sau:
B. z - z = 2a

C. z. z = a2 - b2

D . z2  z

2

/g

ro

A. z + z = 2bi

om

Câu 30. Cho số phức z  m  ( m  3)i, (m  R). Tìm m để z đạt giá trị nhỏ nhất
B. m  3

C. m 

.c

A. m  0

3
2

D. m  

3
2

bo

B. z  15  5i

ok

Câu 31. Tìm số phức liên hợp của số phức z  (2  i )(1 i )(2i  1)2
B. z  1  3i

C. z  5  15i

D. z  5  15i

ce

Câu 32. Tính mô đun c ủa số phức z thoả mãn z.z  3( z  z )  4  3i.
B. z  3

.fa

A. z  2.

C. z  4

D. z  1

w

w

Câu 33. Cho số phức z thoả mãn z  (2  i)  3 . Biết rằng tập hợp các điểm biểu diễn số phức z

w

trong mặt phẳng phức là một đường tròn . Tính diện tích S của đường tròn đó:
A.

S  3

B

S  3

C)

S  6

D.

S  9

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

Câu 34. Cho số phức z  a  bi( a, b R) thoả (1  i)(2 z  1)  ( z  1)(1  i)  2  2i. Tính P  a  b.
D. P  

C. P  1

1
3

H
oc

B. P  1

01

A. P  0

1 3
a .
3

B.

1 3
a .
6

2
D. a 3 .
3

C. a 3 .

uO
nT
hi
D

A.

ai

Câu 35. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cận tại A, AB  AC  a . Chiều cao
SA  2a . Tính thể tích khối chóp S.ABC.

Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB  a, AC  5a . Hai mặt bên

 SAB 

và  SAD  cùng vuông góc với đáy, cạnh bên SB tạo với đáy một góc bằng 600 . Tính theo a

A. 6 2a3 .

ie

thể tích của khối chóp S.ABCD.

C. 2 2a3 .

D. 2a 3 .

iL

B. 4 2a3 .

up

1
B. .
5

1
C. .
3

2
D. .
5

ro

1
A. .
6

s/

Ta

Câu 37. Cho tứ diện ABCD có B’ là trung điểm AB, C’ thuộc đoạn AC và thỏa mãn 2 AC '  C ' C .
Tính tỉ số thể tích giữa khối tứ diện AB’C’D và phần còn lại của khối tứ diện ABCD.

h3 3
.
4

B.

3h3 3
.
4

C.

om

A.

/g

Câu 38. Khối chóp tam giác đều có chiều cao h và cạnh bên bằng 2h . Tính thể tích của khối chóp đó.

9h 3 3
.
4

D.

h3 3
.
12

ok

.c

Câu 39. Cho hình nón có đường sinh l  2a và hợp với đáy góc   600 . Tính diện tích toàn phần
của hình nón.
B. 3 a 2 .

C. 2 a 2 .

ce

bo

A. 4 a 2 .

.fa

Câu 40. Hình chóp tứ giác đều có cạnh đáy bằng 1, chiều cao h bằng

D.  a 2 .

3
. Tính tỉ số thể tích của khối
2

w

cầu nội tiếp khối chóp đã cho và thể tích khối chóp đó.


.
4

B.


.
9

C.


.
2

D.

w

w

A.

www.facebook.com/groups/TaiLieuOnThiDaiHoc01


.
3

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

1
D. .
2

C. 1.

H
oc

B. 3.

A. 2 .

01

Câu 41. Một hình chữ nhật ABCD với AB  AD có diện tích bằng 2, chu vi bằng 6. Cho hình chữ nhật đó
V
quay quanh AB và AD được các khối tròn xoay có thể tích tương ứng là V1 ,V2 . Tính tỉ số 1 .
V2

A. 8 .

B. 6 .

uO
nT
hi
D

ai

Câu 42. Một hình nón có thiết diện qua trục là một tam giác đều. Tính tỉ số thể tích của khối cầu
ngoại tiếp và khối cầu nội tiếp khối nón.
C. 4 .

D. 2 .

Câu 2. Cho hai điểm A(1; –1; 2), B(2; 0; 1) và mặt phẳng (P): x + 2y – 2z – 5 = 0. Tìm tọa độ giao
điểm I của đường thẳng AB và mặt phẳng (P).
B.I (–1; –3; 4)

ie

 x  6  4t

.
 y  2  t
z  1  2t


D. I(0; 2; –1)

Tìm tọa độ hình chiếu vuông góc của A

Ta

Câu 43. Cho điểm A(1; 1; 1) và đường thẳng (d):

C. I(3; 1; 0)

iL

A. I(–2; –6; 8)

A. (2; –3; –1)

up

s/

lên đường thẳng (d).

C. (2; –3; 1)

B. (2; 3; 1)

D. (–2; 3; 1)

/g

ro

Câu 44. Trong không gian với hệ tọa độ Oxyz, cho hình hành ABDC với A(1; 2; 1), B(1;1; 0),

A. (1; –1; 1)

om

C(1; 0;2).Tọa độ đỉnh D là

C. (1; –1; 3)

B. (1; 2; 2)

C. (2; 1; 0)

B. (1; 1; 3)

D. (–1; 1; 1)

bo

A. (1; 1; 0)

ok

.c

Câu 45. Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 1; 2). Tìm điểm N thuộc mặt phẳng
Oxy sao cho độ dài đoạn thẳng MN là ngắn nhất.
D. (2; 2; 0)

ce

Câu 46. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1; 2; 3), B(3; 2; 1). Gọi M là điểm
 

.fa

thuộc mặt phẳng Oxy. Tìm tọa độ của M để P = | MA  MB | đạt giá trị nhỏ nhất.
B. (1; 1; 0)

C. (2; 1; 0)

D. (2; 2; 0)

w

A. (1; 2; 1)

w

w

Câu 47. Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có các điểm A(0; 1; 0), B(0; 1; 1),
C(2; 1; 1), D(1; 2; 1). Thể tích của tứ diện ABCD bằng
A. 1/6

B. 1/3

C. 2/3

D. 4/3

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

B. (0; 1; 3)

C. (0; 2; 3)

D. (0; 1; 2)

H
oc

A. (0; 2; 1)

01

Câu 48. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1; 1; 0), B(3; 0; 5), C(2; 2; 1). Gọi M
là một điểm chạy trên mặt phẳng Oyz. Giá trị của P = MA² + MB² + MC² đạt giá trị nhỏ nhất khi M
có tọa độ là

ai

Câu 49. Trong không gian với hệ tọa độ Oxyz, gọi (P) là mặt phẳng đi qua G(1; 2; –1) và cắt Ox, Oy,
Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC.

uO

nT
hi
D

Viết phương trình mặt phẳng (P).
A. (P): x + 2y – z – 4 = 0

B. (P): 2x + y – 2z – 2 = 0

C. (P): x + 2y – z – 2 = 0

D. (P): 2x + y – 2z – 6 = 0

iL

ie

Câu 50. Trong không gian với hệ tọa độ Oxyz, gọi (P) là mặt phẳng đi qua M(2; 1; 2) và c ắt các tia
Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích của khối tứ diện OABC là nhỏ nhất. Viết phương
trình mặt phẳng (P).
B. (P): x + 2y + z – 6 = 0

C. (P): 2x – y + 2z – 7 = 0

D. (P): x – 2y + z – 4 = 0

up

s/