ĐỀ THI TOÁN 2017 THPT b HAI HAU

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

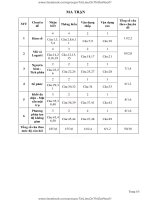
MA TRẬN ĐỀ THI THỬ THPTQG 2017.

Thông hiểu

Vận dụng

Cộng

01

Nhận biết

Cấp

H
oc

độ
Cấp độ cao

Tên

ai

Cấp độ thấp

ứng dụng đạo
hàm để khảo sát
và vẽ đồ thị hàm

số

-Nhận biết được
các đường tiệm cận
của đồ thị hàm số

y

ax  b
cx  d

-Hiểu định lí, quy tắc
xét tính đơn điệu để tìm
khoảng đơn điệu của
hàm số bậc 3

-Vận dụng được
cách giải phương
trình bậc hai và định
lí Vi-ét, công thức
tính khoảng cách
-Phân biệt được các
giữa hai điểm vào
khái niệm cực trị. Hiểu giải quyết bài toán
định lí, áp dụng được tương giao giữa các
quy tắc tìm cực trị .
đồ thị.
-Hiểu được khái niệm
-Vận dụng bài toán
đường tiệm cận của đồ

tìm GTLN, GTNN
thị hàm số.
vào giải quyết vấn
-Áp dụng được quy tắc đề thực tiễn
tìm GTLN, GTNN của
-Vận dụng kiến thức
hàm số.
hình học tọa độ vào
-Biết cách viết phương bài toán cực trị của
số
trùng
trình tiếp tuyến với đồ hàm
phương có tham số.
thị hàm số.

-Vận dụng tính
đơn điệu của
hàm số trong giải
phương trình vô
tỉ

6

3

1

12

1,2

12%

0,6
6%

0,2
2%

3,6
(36%)

Số câu

2
0,4
4%

.c

Tỉ

ok

Số điểm
lệ %

om

/g

ro

up

s/

Ta

iL

ie

-Nhận biết được
dạng đồ thị hàm số
trùng phương

uO
nT
hi
D

chủ đề

-Tìm m để phương -Vận dụng các
trình mũ có nghiệm
kiến thức về các
phép tính logarit,
-Vận dụng kiến thức
phương trình mũ
hàm số mũ vào giải

để giải bài toán
bài toán lãi kép
thực tế.

Số câu

w

w

w

.fa

ce

bo

Hàm số lũy thừa, -Nhận biết được -Áp dụng được công
công thức tính đạo thức tính đạo hàm của
hàm số mũ và
hàm số logarit
hàm của hàm số hàm số mũ
mũ
-Hiểu được tính đơn
-Biết được kí hiệu điệu của hàm số mũ và
logarit thập phân, logarit
logarit tự nhiên
-Biết cách giải một số
-Nhận biết được phương trình mũ và

các tính chất của logarit, bất phương trình
hàm số logarit
logarit đơn giản

Số điểm
lệ %

Tỉ

2

5

2

1

10

0,4
4%

1,0
10%

0,4
4%

0,2
2%

2,0
(20%)

www.facebook.com/groups/TaiLieuOnThiDaiHoc01


www.facebook.com/groups/TaiLieuOnThiDaiHoc01
Nguyên hàm,
tích phân, ứng
dụng

-Biết được nguyên
hàm của một số
hàm số cơ bản

-Hiểu được định nghĩa -Vận dụng việc lấy
và tính chất của tích nguyên hàm
vào
phân
giải bài toán thực tế
-Áp dụng được phương
pháp tính tích phân từng
phần

-Nhận biết được số
phức liên hợp

7

1,6
16%

0,2
2%

-Hiểu được khái niệm -Kết hợp vận dụng
số phức và các khái các phép tính số
niệm liên quan( phần phức, cách giải hệ
thực,
phần
ảo, phương trình vào
modun,...)
việc xác định số
phức
-Thực hiện được các
phép tính số phức

1,4
(14%)

-Vận dụng biểu
diễn hình học
của số phức kết
hợp kiến thức
hình học tọa độ
phẳng
(hoặc
lượng giác) để số
phức có modun

nhỏ nhất

Ta

-Biết biểu diễn hình học
của số phức

iL

ie

Số phức

1

H
oc

Tỉ lệ % 0,4
4%

4

ai

Số điểm

2

uO

nT
hi
D

Số câu

01

Hiểu công thức tính
diện tích hình phẳng,
thể tích khối tròn xoay

Số câu

1

2

Số điểm Tỉ lệ %

0,2
2%

Thể tích khối đa
diện

-Biết được một số
đặc điểm của khối
bát diện đều

0,4
4%

0,2
2%

0,2
2%

1,0
(10%)

-Hiểu được thế nào là
mặt phẳng đối xứng của
một hình

-Vận dụng tính
khoảng cách từ một
điểm tới mặt phẳng

ro

5

/g

om

.c

Thể tích khối
tròn xoay

w
w

Tỉ

1

ok
w

Số điểm
lệ %

1

-Áp dụng được công
thức tính thể tích của
khối chóp

1

2

1

4

0,2
2%

0,4
4%

0,2
2%

0.8
(8%)

-Biết công thức
tính thể tích khối
trụ

-Biết cách xác định tâm,
bán kính mặt cầu nội
tiếp hình lập phương.
Tính được diện tích mặt
cầu

-Vận dụng kiến thức
hình học không gian
tổng hợp vào tính
toán trên khối nón

bo
ce

.fa

Số câu

up

s/

-Biết cách giải phương
trình bậc hai trên tập số
phức

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

-Vận dụng kiến
thức về hình nón,
độ dài cung tròn
vào giải bài toán
thực tế


www.facebook.com/groups/TaiLieuOnThiDaiHoc01

Phương pháp
tọa độ trong
không gian

1

1

4

0,2
2%

0,2
2%

0,2
2%

0,2
2%

0.8
(8%)

-Vận dụng kiến thức
về vị trí tương đối
của mặt cầu và mặt
phẳng vào bài toán
viết phương trình
mặt phẳng có liên
quan đến khoảng
cách nhỏ nhất

-Vận dụng kiến
thức hình học
không gian tổng

hợp vào bài toán
viết phương trình
đường thẳng liên
quan đến khoảng
cách nhỏ nhất

-Biết biểu thức tọa -Biết cách viết phương
độ về các phép trình mặt cầu
toán véc tơ
-Biết cách viết phương
-Đọc được véc tơ trình mặt phẳng
chỉ phương của
-Biết cách sử dụng
đường thẳng khi
phương trình đoạn chắn
cho trước phương
trình

3

1

0,6
6%

0,6
6%

0,2
2%

Tổng số câu

12

23

10

Tổng số điểm
Tỉ lệ %

2,4
24%

4,6
46%

2,0
20%

iL

Tỉ

1

8

0,2

2%

1,6
(8% )

5

50

1,0
10%

10
(100%)

s/

Ta

Số điểm
lệ %

ie

3

uO
nT
hi
D

-Nhận biết được
hai mặt phẳng
vuông góc
Số câu

01

Tỉ

1

H
oc

Số điểm
lệ %

1

ai

Số câu

ĐỀ THI THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA
Năm học 2016-2017
Môn: Toán
Thời gian làm bài: 90 phút

/g

ro

up

Sở GD-ĐT Nam Định
Trường THPT B Hải Hậu

ok

B. y  x 4  2 x 2  1

.c

om

Câu 1. Đường cong trong hình bên là đồ thị của hàm
số nào dưới đây:
A. y  x 4  2 x 2  1
C. y   x 4  2 x 2  1

bo

D. y   x 4  2 x 2  1

ce

Câu 2. Tiệm cận ngang của đồ thị hàm số y 

.fa

A. y  1

B. x  1

w

w

Câu 3. Điểm cực tiểu của đồ thị hàm số y 

w

A. 0

B. 2

3 x
là đường thẳng:
x3
C. x  3

D. y=1

2x  x  1
là:
x 1
2

D.  2; 7 

C.  0;1

2
Câu 4. Cho hàm số y  f  x  có đạo hàm f '  x   x  x  1  x  2  . Số điểm cực trị của hàm số là:
3

4

A. 0

B. 1
C. 2
D. 3
2
2x  3x  2
Câu 5. Cho hàm số y  2
. Khẳng định nào sau đây sai?
x  2x  3
www.facebook.com/groups/TaiLieuOnThiDaiHoc01


www.facebook.com/groups/TaiLieuOnThiDaiHoc01
1
A. Đồ thị hàm số có tiệm cận ngang là y 
B. Đồ thị hàm số có tiệm cận ngang là y  2
2
C. Đồ thị hàm số có ba đường tiệm cận
D. Đồ thị hàm số có hai tiệm cận đứng là x= –1; x=3

x3 x2
3

 6x  . Khẳng định nào sau đây là đúng?
3
2
4
A. Hàm số đồng biến trên khoảng  2; 3 
B. Hàm số nghịch biến trên khoảng  2; 3 



C. Hàm số nghịch biến trên khoảng ; 2





D. Hàm số đồng biến trên khoảng 2; 



H
oc

Câu 7. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 x 3  6 x 2  1 trên đoạn [–1;1] là:
B. 2
A. 7
C. 6
D. 3

01

Câu 6. Hàm số y 

ai

2x  1
có đồ thị (C). Tiếp tuyến với (C) có hệ số góc bằng –5 có phương trình là:
x2
A. y  5x  2; y  5x  22
B. y  5x  2; y  5x  22
C. y  5x  2; y  5x  22

uO
nT
hi
D

Câu 8. Cho hàm số y 

D. y  5x  2; y  5x  22

Câu 9. Biết rằng phương trình

5  x  1 x 

5  x 1  x  

C. (–5;–3)

D. (3;5)

iL

B. (–3;1)

Ta

A. (–1;3)

có hai nghiệm x 1 , x2

ie

(x 1
x
 x6
2

2x  1
tại hai điểm phân biệt A, B sao cho
x 1

AB  2 3

B. m  2  10

D. m  2  3

C. m  4  10

ro

A. m  4  3

up

s/

Câu 10. Tìm m để đường thẳng y  x  m  1 cắt đồ thị hàm số y 

om

/g

Câu 11. Tìm m để đồ thị hàm số y  x 4  2m2 x 2  1 có ba điểm cực trị lập thành một tam giác vuông cân ?
A. m  2
B. m  1
C. m  1
D. m  1

ce

bo

ok

.c

Câu 12.Một đoàn cứu trợ lũ lụt đang ở vị trí A của tỉnh Quảng Bình muốn tiếp cận vị trí C để tiếp tế lương
thực và thuốc phải đi theo con đường từ A đến B và từ B đến C (như hình vẽ). Tuy nhiên do nước ngập con
đường từ A đến B nên đoàn cứu trợ không thể đi đến C bằng xe, nhưng đoàn cứu trợ có thể chèo thuyền từ A
đến vị trí D trên đoạn đường từ B đến C với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h. Biết A cách B
một khoảng 5km, B cách C một khoảng 7km. Xác định vị trí điểm D để đoàn cứu trợ đi đến C nhanh nhất.
A
A. BD  5 km
B. BD  4 km
5 km
C. BD  2 5 km

.fa

D. BD  2 2 km
B

w

7 km

1 2 x

w

w

Câu 13. Đạo hàm của hàm số y  e
A. y '  e

x

C

D

B. y '  e

là

1 2 x

1 2 x

C. y '  2e

1 2 x

D. y '  2e

Câu 14. Cho hàm số y = log x . Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên (0; +)

B. Đồ thị hàm số có tiệm cận đứng là trục tung.

C. Đồ thị hàm số cắt trục hoành tại điểm M(1;0)

D. Đồ thị hàm số luôn nằm phía trên trục hoành.

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01
x 1
Câu 15. Đạo hàm của hµm sè y =
là :
4x
A. y’ =

1  2  x  1 ln 2
22x

1  2  x  1 ln 2
22x

B. y’ =

C. y’ =

1  2  x  1 ln 2
2

x2

D. y’ =

1  2  x  1 ln 2
2x

2

15

A. a>1, 0




2  7  logb



D. 36



2  5 thì:

B. 0
ai

19

Câu 17.Nế u a 5  a 7 và logb

C. 32

H

oc

B. 16

C. 0
D. a>1, b>1

uO
nT
hi
D

A. 12

01

Câu 16.Phương trình log 22 x  5log 2 x  4  0 có 2 nghiệm x1 ,x2 , khi đó tích x 1 .x2 bằng:

Câu 18.Phương trình: 32 x1  4.3x  1  0 có 2 nghiệm x1 và x2 trong đó x1  x2 .Khẳng định nào đúng?
A. 2 x1  x2  0

B. x1  2 x2  1

C. x1  x2  2

D. x1.x2  1

Câu 19.Tập nghiệm của bất phương trình log0,8  x 2  x   log0,8  2 x  4  là :

1)

 (m  1).2x

2

2

 2m  6 có nghiệm khi

B. 2  m  9

C. 2  m  9

D. 2  m  9

Ta

A. 2  m  9

2

D.  4;1  2;

ie

Câu 20. Phương trình: (m  2).22( x

C.  ;4  1;2

iL

A.  ;4  1; B.  4;1

up

s/

Câu 21.Một người gửi 6 triệu đồng vào ngân hàng theo hình thức lãi kép, kì hạn một năm với lãi suất 7,56%
một năm. Hỏi sau bao nhiêu năm người đó sẽ có ít nhất 12 triệu đồng từ số tiền gửi đó?
B.10

A. 9

C. 8

D. 7

om

/g

ro

Câu 22. Cường độ một trận động đất M (richter) được cho bởi công thức M = logA – logA0 , với A là biên độ
rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỉ XX, một trận động đất ở San Francisco có
cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở Nam Mỹ có biên độ rung chấn mạnh hơn
gấp 4 lần. Cường độ trận động đất ở Nam Mỹ là:
B.33,2

 2  3x 

2

C

ok

1

B. 

3

 2  3x 

ce

A.

dx
bằng:
2  3x

bo

Câu 23. 

C. 2,075

2

C

1
C. ln 2 3 x  C
3

Câu 24.Nguyên hàm của hàm số f  x   3sin x 

.fa

D. 11

.c

A. 8,9

1
D.  ln 3x  2  C
3

2
cos2 x

3
 2cos x  2 tan x   C
2
3
3

C.   2cos x  2 tan x   C D.  2cos x  2 tan x   C
2
2
1
Câu 25.Hàm số y  f ( x) có đạo hàm là f /  x  
và f (1)  1 thì f (5) bằng:
2x  1
A. ln3 + 1
C. ln2 + 1
D. ln2 + 1
B. ln2

w

w

w

A. 3cos x  2 tan x  C B. 

www.facebook.com/groups/TaiLieuOnThiDaiHoc01


www.facebook.com/groups/TaiLieuOnThiDaiHoc01
1
1
Câu 26. Biết  x2 ln xdx   4 ln a   . Hỏi 3a – 4b bằng
3
b
1

2

A. 0

B.1

C. 2

D. 3

H
oc

01

Câu 27. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y  x 2  2 x , y  x là
9
9
13
7
A.
B.
C.
D.
4
4
4
2
Câu 28. Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi đồ thị hàm số y  tan x, hai trục tọa độ,


đường thẳng x  khi quay quanh trục Ox.
4

A.

4000
m
3

B.

1900
m
3

C.

4300
m
3

D.

Câu 30. Số phức z thỏa mãn: z  4  2i là:

Câu 31. Cho số phức z thỏa mãn: z 

C. z  4  2i

D. z  2  4i

ie

B. z  2  4i

2200
3

(1  3i)3
. Tìm môđun của z  iz .
1 i

iL

A. z  2  4i

uO
nT
hi
D

ai

2
2
2
2
A.  
B.  
C.  

D.  
5
4
3
2
Câu 29. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc a(t) = 3t + t2 (m/s2 ). Quãng
đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc là bao nhiêu?

om

/g

ro

up

s/

Ta

A. 8 2
B. 8 3
C. 4 2
D. 4 3
2
Câu 32. Gọi z1 , z2 là hai nghiệm phức của phương trình z  2z  10  0 . Tính giá trị của biểu thức
A  | z1 |2  | z 2 |2 .
A. 15.
B. 17.
C. 19.

D. 20
2
Câu 33.Cho số phức z thỏa mãn: (2  3i)z  (4  i)z  (1  3i) . Xác định phần thực và phần ảo của z.
A. Phần thực – 2 ; Phần ảo 5i.
B. Phần thực – 2 ; Phần ảo 5.
C. Phần thực – 2 ; Phần ảo 3.
D. Phần thực – 3 ; Phần ảo 5i.
Câu 34. Cho số phức z thỏa mãn z  3  4i  4 . Giá trị nhỏ nhất của z bằng:

1
1
D.
3
2
Câu 35. Mỗi đỉnh của một hình bát diện đều là đỉnh chung của bao nhiêu cạnh.
B. 1

C.

B.Bốn cạnh

bo

A. Năm cạnh

ok

.c

A. 2

C. Ba cạnh

ce

Câu 36. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ?
A. 1
B. 2
C. 3

D. Sáu cạnh
D. 4

w

w

w

.fa

Câu 37. Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a; Góc A bằng 600 . O là tâm hình thoi. SA
vuông góc với đáy. Góc giữa SO và đáy bằng 450 . Tính theo a thể tích khối chóp SABCD
a3
a3
A. a 3
B.
C.
D. 2a 3
4

2
Câu 38. Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA  a 3 và vuông góc với đáy. Tính
khoảng cách từ trọng tâm G của tam giác SAB đến mặt phẳng (SAC) bằng:
a
a 2
a 3
a 3
A.
B.
C.
D.
6
2
6
2
Câu 39. Cho hình lập phương có cạnh bằng a .Tính diện tích mặt cầu tiếp xúc với các mặt của hình lập
phương.
www.facebook.com/groups/TaiLieuOnThiDaiHoc01


www.facebook.com/groups/TaiLieuOnThiDaiHoc01
A. 2 a
B. 8 a 2
C.  a 2
D. 4 a 2
Câu 40. Thể tích của khối trụ có bán kính đáy r  2cm và chiều cao h  9cm là
A. 18 cm3
B. 18cm3
C. 162 cm3
D. 36 cm3

Câu 41.Cho khối nón có đỉnh S, cắt khối nón bởi một mặt phẳng qua đỉnh của khối nón tạo thành thiết diện là
tam giác SAB. Biết khoảng cách từ tâm của đường tròn đáy đến thiết diện bằng 2, AB = 12, bán kính đường
tròn đáy bằng 10. Chiều cao h của khối nón là:
2

01

8 15
2 15
4 15
B.
C.
D. 15
15
15
15
Câu 42. Bình có một tấm bìa hình tròn như hình vẽ, bạn ấy muốn biến hình tròn đó thành một hình cái phễu
hình nón. Khi đó Bình phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB lại với nhau. Gọi x là
góc ở tâm hình quạt tròn dùng làm phễu. Tìm x để thể tích phễu lớn nhất ?

uO
nT
hi
D

ai

H
oc

A.




2 6

B.
C.
D.
3
2
4
3
Câu 43. Cho mặt phẳng (P): 2x + y = 0. Mặt phẳng nào dưới đây vuông góc với (P)
A. x –y + z + 1 = 0
B. x–2y + z –1 = 0
C. 2x –y + z – 1 = 0
D. –2x –y = 0

Ta

iL

ie

A.



B.

x 1
y
z2


4
2
6

up

x
y 3 z


2
1
3

C.

x  2 y 1 z  3


1
3
2

D.

x y z


3 1 2

ro

A.

s/

Câu 44.Vectơ a = (2; –1; 3) là vectơ chỉ phương của đường thẳng nào sau đây:

B. (3; 3; –1)

om

A. (0; –3; 4)

/g




  

Câu 45.Cho a = (2; –3; 3), b = (0; 2; –1), c = (1; 3; 2). Tìm tọa độ của vectơ u  2a  3b  c

C. (3; –3; 1)

D. (0; –3; 1)

Câu 46.Cho I (4; 1; 2), A(1; 2; 4) , phương trình mặt cầu (S) có tâm I và đi qua A là:
2

.c

A. ( x  4) 2   y  1  z  2  46
2

C. ( x  4) 2   y  1  z  2  46

ok

2

2

B. ( x  1) 2   y  2  z  4  46
2

2

D. ( x  4) 2   y  1  z  2  46
2

2

ce

bo

Câu 47.Viết phương trình mặt phẳng (P) đi qua ba điểm A(2; 0; 0), B(0; –1; 0), C(0; 0; –3).
A. –3x + 6y + 2z + 6 = 0
B. –3x – 6y + 2z + 6 = 0
C. –3x – 6y + 2z – 6 = 0
D. –3x + 6y – 2z + 6 = 0

.fa

Câu 48. Cho A(1;0;-2), B(0;-4;-4) và mặt phẳng (P): 3x  2 y  6 z  2  0 . Phương trình mặt phẳng (Q) chứa
đường thẳng AB và  (P) là:

w

A. 2x – y – z – 4 = 0

B. 2x + y – z – 4 = 0

C. 2x – z – 4 = 0

D. 4x + y –4 z – 12 = 0

2
Câu 49.Trong không gian Oxyz cho mặt cầu (S): (x  1)   y  1   z  3  14 và điểm M(–1;–3;–2). Lập

w

w

2

2

phương trình mặt phẳng (P) đi qua M, cắt (S) theo một đường tròn có bán kính nhỏ nhất.
A. 2y – z + 4 = 0

B. x – 2y – 5 = 0

C. 2x – z = 0

D. y + 2z +7 = 0

www.facebook.com/groups/TaiLieuOnThiDaiHoc01


www.facebook.com/groups/TaiLieuOnThiDaiHoc01
x 1 y z 1
Câu 50.Trong không gian Oxyz cho điểm A(1;1;1) và đường thẳng d:
. Viết phương trình


1
2
1

x 1 y 1 z 1



1
7
1

B.

x 1 y  3 z


2
2
1

C.

x  3 y 1 z  4


2
2
5

D.

x 1 y 1 z 1


1
2

1

w

w

w

.fa

ce

bo

ok

.c

om

/g

ro

up

s/

Ta

iL

ie

uO
nT
hi
D

ai

H
oc

A.

01

đường thẳng d’ đi qua A, cắt d sao cho khoảng cách từ điểm O đến d’ nhỏ nhất.

www.facebook.com/groups/TaiLieuOnThiDaiHoc01