ĐỀ THI TOÁN 2017 THPT AN PHUC

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (612.81 KB, 9 trang )

www.facebook.com/groups/TaiLieuOnThiDaiHoc01
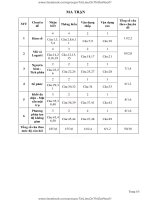
I. MA TRẬN ĐỀ THỬ NGHIỆM THI THPT QUỐC GIA NĂM 2017
TRƯỜNG THPT AN PHÚC
MỨC ĐỘ

2

0.8

Hàm số lũy 3
thừa – Hàm
số mũ – Hàm
số logarit

0.4
3

0.6

Nguyên hàm 2
– Tích phân
- Ứng dụng

2

0.6
3

2

2

1

3

Tọa độ trong
không gian

3

2

2

0.6

2

0.6

0.4
14

up

TỔNG

12

2.8

1.6

1

8
1.6

0.2

50

7

2.4

1.4

10.0

ro

3.4

8

0.2

0.4

s/

17

1.2

0.2

0.4

1.4

6

1

0.4
2

0.2

0.2

Ta
iL

Hình không
gian tổng
hợp

7

1

0.4

2.0

0.2

0.4

Số phức

0.4

10

1

0.4

2.2

0.4

0.6
2

0.4

11

1

0.6
2

TỔNG

ai
H
oc
01

3

VD CAO

D

4

VD THẤP

ie
uO
nT

Ứng dụng

của đạo hàm

THÔNG HIỂU

hi

NHẬN
BIẾT

CHỦ ĐỀ

om
/g

II. ĐỀ THI THỬ NGHIỆM THPT QUỐC G IA 2017
Câu 1. Cho hàm số y =  x3  x2 + 5x + 1. Mệnh đề nào sau đây đúng?

bo

ok

.c

5
A. Hàm số nghịch biến trên   ;1 .
 3 




5

ce

C. Hàm số đồng biến trên  ;   .
3


w

.fa

Câu 2. Tiệm cận ngang của đồ thị hàm số y 

w

w

A. y =  2.
C. y 

1
3

B. y 

5
B. Hàm số đồng biến trên   ;1 .
 3 

D. Hàm số đồng biến trên 1;   .
2x  1
là:
3 x

2
.
3

D. y = 2.

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01
Câu 3.Cho hàm số y = f(x) xác định và liên tục trên  2; 2 và có đồ thị như hình vẽ 1 bên. Hàm số

f(x) đạt cực đại tại điểm nào dưới đây?

y

A. x =  2.

3

B. x = 0.
1

C. x = 1.
0

-1

D. x = 2.

ai
H
oc
01

-2

-1

Câu 4. Biết rằng đồ thị hàm số y 

x3
và đường thẳng y
x 1

=x  2

-2

C. yA + y B = 4.

D. yA + y B = 0.

hi

B. yA + y B = 2.

D

cắt nhau tại hai điểm phân biệt A(xA ; y A) và B(xB ; y B). Tính yA + y B.
A. yA + y B =  2.

x

2

–

x

2

y’

5

–

+

0

8

–

2

+

0

up

s/

0

+

+

Ta
iL

+

y

ie
uO
nT

Câu 5. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:

ro

Phát biểu nào sau đây đúng?

om
/g

A. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 2.
B. Giá trị cực đại của hàm số bằng 5.

.c

C. Hàm số có đúng một điểm cực trị.

ok

D. Hàm số đạt cực tiểu tại x = 2 và x = 8.
Câu 6.Đồ thị hàm số sau là của hàm số nào sau đây?

bo

y

A. y = x4  2x2 3.

ce

x

B. y = x + 8x  9.

2

-

-1

0

1

.fa

4

w

C. y =  x4 + 2x2 + 3.

w

D. y = x3  2x2 + 4x  1.

w

-3
-4

Câu 7. Tìm m để đồ thị hàm số y 

x 1

có hai tiệm cận đứng.
x  mx  2
2

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

A. m  3 .



 





B. m ; 2 2  2 2; 



 



C. m ; 2 2  2 2;  \ 3 .



D. m  2 2; 2 2 .

Câu 8. Tìm m để hàm số y = x4  2mx2 + 3 có ba điểm cực trị.
B. m  0 .

C. m < 0.

D. m > 0.

Câu 9. Tìm m để phương trình x3 3x2 + m  1 = 0 có ba nghiệm phân biệt.
B.  1 < m < 5.

mx  4
đồng biến trên khoảng 1;   .
xm

m  2

A.  2 < m < 2.

D. 1  m  5 .

D

Câu 10. Với giá trị nào của m thì hàm số y 

C. 1  m  5 .

C. m > 2.

D. m < 2.

ie
uO
nT

B. 
.
 m  2

hi

A. 1 < m < 5.

ai
H
oc
01

A. m  0 .

Ta
iL

Câu 11. Cho một tấm bìa hình vuông c ạnh 5 dm. Để làm một mô hình kim tự tháp Ai Cập, người ta
cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp lên, ghép lại
thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình là:
A.

3 2
.
2

B.

C.

5 2
.
2

D. 2 2 .

s/
up
ro

om
/g

1

 2  3x dx là:
B.

1
ln | 2  3x | C
2

C. -3ln|2-3x|+C

D.

1
ln | 2  3x | C
3

ok

A.ln|2-3x|+ C

.c

Câu 12.

5
.
2

ce

1
e

B. 1 

1
e

C. 1 

1
e

D. 1 

1
e

.fa

A. 1 

bo

Câu 13. F(x) là một nguyên hàm của f ( x)  e1 x và F(1) = 0. Tính F(2).

3

Câu 14. Gọi F(x) là một nguyên hàm của f(x) trên [2;3] ; F(3)= 3; F(2) = 2.Tính

2

w
w
w

A. -1

 f ( x)dx .

B. 1

C. 5

D. 6
2

e3 x
ex
Câu 15. Cho F là một nguyên hàm của hàm số y  trên (0; ) . Đặt I   dx , khi đó ta có:
x
x
1
A. I 

F (6)  F(3)
3

C. I=3[ F(6) – F(3)]

B. I= F(6) – F(3)
D.I=3[ F(6) – F(1)]
www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

4

Câu 16. Biết

2
, với a.b là các số nguyên. Tính S  a  b .
2

 sin 3 x.sin 2 xdx  a b
0

A.

1
6

B.

3
10

C.

3
10

1
5

D.

A.

31
3

B.

34
3

C.

34
3

D.

ai
H
oc
01

Câu 17. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  4 x  x 2 và trục Ox là:
33
3

Câu 19. Biểu thức

A.

7
x3

D. 6,5m

x . 3 x . 6 x5 (x > 0) viết dưới dạng luỹ thừa với số mũ hữu tỷ là:

B.

5
x2

C.

2
3
x

B.

C. x  x 2  1

x2  1

D.

x

x  x2  1

up

x  x2  1

1

s/

1

5
x3

D.

Câu 20. Đạo hàm của hàm số y = ln(x+ x 2  1 ) bằng
A.

hi

C. 4,5m

ie
uO
nT

B. 5,5m

Ta
iL

A. 3,5m

D

Câu 18. Một ô tô đang chạy với vận tốc 18m/s thì người lái xe hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc v(t) = -36t+18(m/s) trong đó t là khoảng thời gian tính bằng giây kể từ lúc
bắt đầu hãm phanh. Hỏi từ lúc ô tô hãm phanh đến khi dừng hẳn, ô tô di chuyển bao nhiêu m?

6
7

B.

2
3

C.

4
5

D. 2

om
/g

A.

ro

Câu 21. Phư¬ng tr×nh 42x3  84x cã nghiÖm lµ:

ok

1 
C.  ;3 
2 

 6
B. 1; 
 5

D.  3;1

bo

A. (0; +)

.c

Câu 22. Bất phương trình: log2  3x  2   log2  6  5x  có tập nghiệm là:

ce

Câu 23. Tìm m để phương trình 4 x  2 x3  3  m có đúng 2 nghiệm x  1;3
B. 3 < m < 9.

C. - 9 < m < 3.

D. - 13 < m < 3.

.fa

A. - 13 < m < - 9.

w

w

Câu 24. Một người gửi ngân hàng 150 triệu đồng theo thể thức lãi kép lãi suất 0,580 /0 1 tháng. Sau ít nhất
bao nhiêu tháng người đó có 180 triệu đồng?

w

A. 34

B. 32

C. 31

D. 30

C©u 25. Cho a > 0 vµ a  1, x vµ y lµ hai sè d¬ng. T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
A. loga

x loga x

y loga y

C. loga  x  y   loga x  loga y

B. log a ( xy)  log a x.log a y
D. logb x  logb a.loga x

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

Câu 26. NÕu loga x 

A.

2
5

1
loga 9  loga 5  loga 2 (a > 0, a  1) th× x b»ng:
2

B.

3
5

C.

6
5

D. 3

C. log 6 35 

B. log 6 35 

b  3cb
ab  c

D. log 6 35 

3(ac  b)
1 c

abc
1 a

Câu 28. Cho ba số thực dương a, b, c khác 1.

D

ac  ab
abc

y

cho trong hình vẽ bên. Mệnh đề nào dưới đây

y=cx

đúng?
A. a  b  c .

y=ax

x

ie
uO
nT

y=b

Đồ thị các hàm số y  a x , y  b x , y  c x được

hi

A. log 6 35 

ai
H
oc
01

Câu 27. Đặt log 27 5  a, log 8 7  b, log 23  c . Hãy biểu diễn log 635 theo a, b, c.

Ta
iL

1

B. a  c  b .

x

O

up

s/

C. b  c  a .

ro

D. c  a  b .

om
/g

Câu 29.Điểm M trong hình vẽ bên là điểm biểu diễn số
nào sau đây đúng?
B. z  3  2i .

C. z  2  3i .

D. z  2  3i .

y

M

3

ok

.c

A. z  3  2i .

phức z. Khẳng định

x
0

ce

bo

-2

.fa

Câu 30. Cho số phức z = 1 + 2i. Phần ảo của số phức w  2z  z là:
B.  2.

C. 3.

D.  3.

C. z  2  2i .

D. z  2  2i .

w

A. 2.

w

w

Câu 31. Tìm số phức z thỏa mãn z  3i  (5  2i)i .
A. z  2  2i .

B. z  2  2i .

Câu 32. Phương trình z2 + az + b = 0 có một nghiệm phức z = 1 + 2i. Tổng hai số a và b bằng:
A. 0.

B.  4.

C.  3.

D. 3.

Câu 33. Gọi z1, z2 là các nghiệm phức của phương trình z2 + 2z + 4 = 0. Tính A  z1  z2
2

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

2

.

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

B. A =  7.

A. A = 2.

C. A = 8.

D. A = 4.

Câu 34. Trong các số phức z thỏa mãn z  z  3  4i , số phức có mô đun nhỏ nhất là:
3
2

B. z =  3  4i.

A. z = 3 + 4i.

3
2

C. z   2i .

D. z   2i .

2
SBC có diện tích bằng a 7 . Thể tích khối chóp S.ABC là

4

A.

a3 3
6

B.

a 3 21
48

a3 3
12

C.

D.

a3 3
16

ai
H
oc
01

Câu 35: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy và tam giác

D

Câu 36: Cho khối tứ diện ABCD có thể tích bằng 36. Ta lấy điểm M nằm trên đoạn AB với

ie
uO
nT

A. 3

hi

AM 1
AN 1
 , N nằm trên đoạn AC với
 . Thể tích của khối AB’C’D là:
AB 3
NC 3

B. 4

C. 6

D. 9

1 2
a 3

2

B.

1 2
a 2
3

C.

1 2
a 3
3

D.  a 2 3

s/

A.

Ta
iL

Câu 37. Một hình tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón, ba đỉnh còn lại nằm
trên đường tròn đáy của hình nón. Khi đó diện tích xung quanh c ủa hình nón là :

B.6

C. 2 3

D. 1

w

w

w

.fa

ce

bo

ok

.c

om
/g

Câu 39: Cho bốn hình sau đây:

ro

A.2

up

Câu 38. Hình trụ có bán kính đáy bằng 2 3 và thể tích bằng 24 . Chiều cao hình trụ này bằng

Mệnh đề nào sau đây SAI ?
A. Khối đa diện A không phải là khối đa diện đều
B. Khối đa diện B là khối đa diện lồi

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

C. Khối đa diện C là khối đa diện lồi
D. Cả 4 khối đa diện A, B, C, D đều là khối đa diện lồi.
Câu 40: Khối lăng trụ ABC. ABC có đáy là tam giác đều, a là độ dài cạnh đáy. Góc giữa cạnh bên
và đáy là 30o . Hình chiếu vuông góc của A trên mặt  ABC  trùng với trung điểm của BC . Thể tích
của khối lăng trụ đ? cho là
a3 3
B.
8

a3 3
C.
3

a3 3
D.
12

ai
H
oc

01

a3 3
A.
4

A. 91125 (cm3 )

A

4

B. 91125 (cm3 )
2

M

s/



(cm3 )

B

13500. 3

Ta
iL



(cm3 )

N

C

om
/g

ro

D.

108000 3

P

up

C.

Q

ie
uO
nT

hi

D

Câu 41: Câu 45: Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn
hình tam giác đều ABC có cạnh bằng 90 (cm). Bạn muốn cắt mảnh tôn hình chữ nhật MNPQ từ
mảnh tôn nguyên liệu ( với M, N thuộc cạnh BC; P và Q tương ứng thuộc cạnh AC và AB) để tạo
thành hình trụ có chiều cao bằng MQ. Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được
là:

Câu 42: Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng 4 . Diện tích của mặt cầu
ngoại tiếp hình chóp S.ABC là
4 2
r
3

.c

B. 4 r 2

C. 24

ok

A.

D. 12

Câu 43. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu  S  :  x 1   y  5   z  3   4 . Tìm
2

2

bo

2

ce

tọa độ tâm I và tính bán kính R của mặt cầu  S  .

.fa

A. I  1;5; 3 , R  16

B. I 1; 5;3 , R  16

C. I  1;5; 3 , R  2

D. I 1; 5;3 , R  2

w

Câu 44. Trong không gian với hệ tọa độ Oxyz , cho điểm M  3; 4;1

w

w

  : 4x  y  2z  7  0 . Viết phương trình mặt phẳng  P  đi qua điểm
  .

và mặt phẳng

M và song song với mặt phẳng

A.  P  : 4 x  y  2 z  18  0

B.  P  : 4 x  y  2 z  18  0

C.  P  : 3x  4 y  z  18  0

D.  P  : 3x  4 y  z  18  0

www.facebook.com/groups/TaiLieuOnThiDaiHoc01

www.facebook.com/groups/TaiLieuOnThiDaiHoc01
x 1 y  3 z  5
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng    :
. Hỏi điểm


1
2
1
nào sau đây không thuộc đường thẳng    .

A. P 1;2; 1

C. M  0;5;4

B. Q  1;3;5

D. N  2;1;6

Câu 46. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A 1;0;2 , B  4;1;6 , C  0;2;1 .

B. AG  6

A. AG  3

ai
H
oc
01

Gọi G là trọng tâm của tam giác ABC . Tính độ dài đoạn AG .
C. AG  3 2

D. AG  2

Câu 47. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : 2 x  y  2 z  9  0 . Viết phương
trình mặt cầu  S  có tâm I  4; 2;1 và tiếp xúc với mặt phẳng   .

B.  S  :  x  4   y  2   z  1  49

C.  S  :  x  4   y  2   z  1  7

D.  S  :  x  4   y  2   z  1  7

2

2

2

2

2

2

2

2

hi

2

2

ie
uO
nT

2

D

A.  S  :  x  4   y  2   z  1  49

2

Ta
iL

 x  1  2t

Câu 48. Trong đường thẳng  d  :  y  2  4t và mặt phẳng  P  : x  y  z  1  0
 z  3t


Khẳng định nào sau đây là đúng ?
A.  d    P 

up

s/

B.  d  cắt (P) tại điểm M(1;-1;-1)
D.  d  / /  P 

ro

C. (d) cắt (P) tại điểm M(-1;-2;2)

om
/g

Câu 49. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;2;5  và đường thẳng
x 3 y z 2
. Viết phương trình đường thẳng  d  đi qua điểm M , đồng thời đường thẳng
 
1
1
1
 d  cắt và vuông góc với đường thẳng    .

x  1 t

B.  y  2  2t
z  5  t


 x  1  2t

C.  y  2  2t
z  5


ok

bo

 x  1  3t

A.  y  2
 z  5  2t


.c

 :

x  1 t

D.  y  2  3t
 z  5  2t


ce

Câu 50: Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A(1;1; 1) , B(1;1;2) , C(1;2; 2) và

w

.fa

mặt phẳng (P): x  2 y  2z  1  0 . Viết phương trình mặt phẳng ( ) đi qua A, vuông góc với mặt
phẳng (P), cắt đường thẳng BC tại I sao cho IB  2IC .
B. 2 x  y  2z  1  0 , 2 x  3y  2z  3  0

C. 2 x  y  2z  3  0 , 2 x  3y  2z  3  0

D. 2 x  y  2z  1  0 , 2 x  3y  2z  3  0

w

w