Tiet 68: On tap cuoi nam (t1)

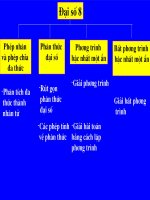
Đại số 8
Phép nhân
và phép chia
đa thức
Phân thức
đại số
Phương trình
bậc nhất một ẩn
Bất phương trình
bậc nhất một ẩn
-
Phân tích đa
thức thành
nhân tử
-
Rút gọn
phân thức
đại số
-
Các phép tính
về phân thức
-
Giải phương trình
-
Giải bài toán
bằng cách lập
phương trình
Giải bất phương
trình

Bài tập trắc nghiệm
Bài 1: Nối thích hợp các đa thức ở cột A với các đa thức ở cột B để
được kết quả phân tích đa thức thành nhân tử
A
B Kết quả
1) x(y - 1) + (y 1) =
2) x(y 1) + y(1 y)=
4) x
2
x - y
2
y = d) (y 1)(x + 1)
a) (y 1)(x y)
b) (x 2y)(x
2
+ 2x y + 4y
2
)
3) x
3
8 y
3
c) (x + y)(x y -1)
e) (x 2y)(x
2
- 2x y + 4y
2
)

Bài tập trắc nghiệm

Bài 1: Nối thích hợp các đa thức ở cột A với các đa thức ở cột B để
được kết quả phân tích đa thức thành nhân tử
A
B Kết quả
1) x(y - 1) + (y 1) =
2) x(y 1) + y(1 y)=
4) x
2
x - y
2
y =
d) (y 1)(x + 1)
a) (y 1)(x y)
b) (x 2y)(x
2
+ 2x y + 4y
2
)3) x
3
8 y
3
c) (x + y)(x y -1)
e) (x 2y)(x
2
- 2x y + 4y
2
)
1 - d
2 - a
3 - b

4 - c

4) x
2
– x - y
2
– y =
= ( x + y)(x – y) - ( x + y)
= ( x + y) (x – y - 1)
(x
2
- y
2
) – ( x + y)

Bài 2: Phân tích đa thức thành nhân tử:
a) 2a
3
54b
3
b)a
2
- b
2
4a + 4
c) x
2
+ 2x - 3
Bài 3: Chứng minh (4n + 3)
2

25 chia hết cho 8
với mọi số nguyên n
Lời giải:
Có (4n + 3)
2
25 = (4n + 3 + 5)(4n + 3 5)
= (4n + 8)(4n 2)
= 8(n + 2)(2n 1)
Vì n là số nguyên nên (n +2)(2n 1) là số nguyên
Do đó 8(n + 2)(2n 1) chia hết cho 8.
Vậy (4n + 3)
2
25 chia hết cho 8 với mọi số nguyên n