ung dung cua tich phan1

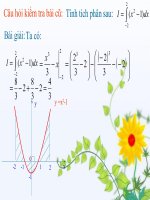
Câu hỏi kiểm tra bài cũ:
Tính tích phân sau:
Bài giải:
Ta có:
( )
( )








−−
−
−








−=−=
−
2
3
2

2
3
2
3
3
3
2
2
3
x
x
3
4
2
3
8
2
3
8
=−+−=
-1
1
2
-2
-1
y =x
2
-1
0
x

y
∫
−
−=
2
2
2
)1( dxxI
∫
−
−=
2
2
2
)1( dxxI


BÀI 3:ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
1.Hình phẳng giới hạn bởi một đường cong và trục hoành
I.TÍNH DIỆN TÍCH HÌNH PHẲNG
2.Hình phẳng giới hạn bởi hai đường cong
II.TÍNH THỂ TÍCH
1. Tính thể tích của vật thể
2. Thể tích của khối chóp và khối chóp cụt
III. THỂ TÍCH CỦA KHỐI TRÒN XOAY


BÀI 3:ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
I.TÍNH DIỆN TÍCH HÌNH PHẲNG
1.Hình phẳng giới hạn bởi một đường cong và trục hoành

Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
y = f(x) liên tục trên trục hoành và hai đường thẳng x = a
x = b được tính theo công thức
( )
∫
=
b
a
dxxfS
Ví dụ 1:
Tính diện tích hình phẳng trong các trường hợp sau:
a. Đồ thị của hàm số y = x
2
, trục hoành và hai đường thẳng x
= -2, x = 1
b. Đồ thị của hàm số y = x
3
- 1, trục hoành và hai đường
thẳng x = 0, x = 2
-1
1
2
-2
-1
y =x
2
-1
0
x
y

BÀI 3:ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
Bài giải ví dụ 1:
Ta có:
∫∫
−
==
1
2
2
)( dxxdxxfS
b
a
Hàm số y= x
2
luôn dương với mọi x do đó
1
2
3
1
2
2
3
−
−
==
∫
x
dxx

1
-2
y =x
2
0 x
y
3
3
8
3
1
=+=
( )
3
2
3
1
3
3
−
−=
(đvdt)
Diện tích hình phẳng đã cho là:
a.


BÀI 3:ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
Ta có :
]1;0[
và

01
3
≤−x
trên đoạn
01
3
≥−x
trên đoạn
]2;1[
Diện tích hình phẳng đã cho là:
∫∫
−==
2
0
3
1)( dxxdxxfS
b
a
( ) ( )
∫∫
−+−−=
2
1
3
1
0
3
11 dxxdxx
2
1

4
1
0
4
44








−+








−−= x
x
x
x
2
7
2
1

4 =−=
(đvdt)








−−








−+








−−= 1
4

1
2
4
2
1
4
1
444
0 x
1
y
y =x
3
-1
2
b.