Tiểu luận Tích phân Lebesgue và qua giới hạn dưới dấu tích phân

MỤC LỤC
DANH SÁCH NHĨM 1 LỚP DT14STH01.......................................................................................................1
MỞ ĐẦU................................................................................................................................................................2
Chương 1: TÍCH PHÂN LEBESGUE...............................................................................................................3
1. Lý do chọn đề tài..............................................................................................................................................3
2. Mục đích nghiên cứu........................................................................................................................................3
3. Phạm vi nghiên cứu..........................................................................................................................................4
4. Phương pháp nghiên cứu.................................................................................................................................4
NỘI DUNG............................................................................................................................................................5
1. Tư tưởng tích phân Lebesgue.........................................................................................................................5
2. Các định nghĩa tích phân.................................................................................................................................5
2.1. Định nghĩa.....................................................................................................................................................5
2.2. Định lí..............................................................................................................................................................7
3. Các tính chất sơ cấp.........................................................................................................................................8
3.1. Tính chất (giả sử các tích phân có nghĩa )..................................................................................................8
3.2. Tính chất (Khả tích ).................................................................................................................................12
4. Bài tập..............................................................................................................................................................13
Chương 2:

QUA GIỚI HẠN DƯỚI DẤU TÍCH PHÂN...........................................................................15

1. Lý do chọn đề tài:...........................................................................................................................................15
2. Mục đích nghiên cứu......................................................................................................................................15
3. Phạm vi nghiên cứu........................................................................................................................................16
4. Phương pháp nghiên cứu...............................................................................................................................16
NỘI DUNG..........................................................................................................................................................17
1. Định lí Lêvi.....................................................................................................................................................17
2. Định lí về sự hội tụ đơn điệu.........................................................................................................................20
3. Định lí Lebesgue về sự hội tụ bị chặn...........................................................................................................20
4. Một số phương pháp tính tích phân Lebesgue...........................................................................................22
4.1. Định lí 4.1 (định lí so sánh).........................................................................................................................22

4.2. Bài tốn tích phân......................................................................................................................................23
KẾT LUẬN..........................................................................................................................................................32
TÀI LIỆU THAM KHẢO.................................................................................................................................33


DANH SÁCH NHÓM 1 LỚP DT14STH01
1. Đào Duy An (100%)
2. Trần Vũ Bảo (100%)
3. Nguyễn Thị Bình (100%)
4. Trần Thị Kim Chung (100%)
5. Hồ Văn Dũng (100%)
6. Phạm Như Duy (100%)
7. Nguyễn Thị Hữu Duyên (100%)
8. Nguyễn Thị Mỹ Duyên (100%)
9. Võ Thị Mỹ Duyên (100%)
10. Đỗ Trọng Đại (100%)
11. Lê Lương Hoàng Đại (100%)
12. Nguyễn Thị Lệ Giang (100%)
13. Nguyễn Thị Ngọc Giàu (100%)
14. Trương Thị Hạnh (100%)
15. Phan Thanh Hậu (100%)
16. Nguyễn Thị Thu Hiền (100%)

Trang 1


MỞ ĐẦU
Ở chương trình phổ thơng, chúng ta đã bước đầu làm quen với khái niệm tích
phân và những ứng dụng hữu ích của nó. Khi đó, phép lấy tích phân của những hàm
liên tục hoặc gián đoạn tại hữu hạn điểm được thực hiện một cách dễ dàng bằng tích

phân Riemann. Thế nhưng, đối với những hàm gián đoạn tại vơ số điểm hoặc tất cả
các điểm thì làm thế nào để có thể lấy tích phân theo một nghĩa nào đó? Đây là một
câu hỏi đã được đặt ra trong suy nghĩ của chúng tôi suốt thời phổ thơng. Khi bước vào
đại học, chúng tơi đã có cơ hội để trả lời câu hỏi đó qua việc tìm hiểu về tích phân
Lebesgue. Tuy nhiên, trong khn khổ của một mơn học, chúng tơi khơng có điều
kiện để nghiên cứu sâu về các tính chất cũng như các điều kiện khả tích của loại tích
phân này trong những trường hợp khác nhau.
Tích phân Riemann trong được giảng dạy cho sinh viên năm thứ hai khoa Toán,
trường đại học Quảng Nam. Tích phân này có nhiều hạn chế đáng kể khi tiếp cận với
một số lĩnh vực cơ bản của Giải tích hiện đại.Vì vậy, mục đích chính của đề tài này là
mở rộng tích phân Riemann tới tích phân Lebesgue của các hàm đo được trong khơng
gian có độ đo.
Vì vậy, chúng tơi đã quyết định chọn “Tích phân Lebesgue và qua giới hạn dưới
dấu tích phân” để làm đề tài tiểu luận của mình.
Bài tiểu luận gồm hai chương:

 Chương 1: Tích phân Lebesgue
 Chương 2: Qua giới hạn dưới dấu tích phân

Trang 2


Chương 1: TÍCH PHÂN LEBESGUE
1. Lý do chọn đề tài
Ý tưởng chính của phép xây dựng tích phân Lebesgue là ta khơng nhóm những
điểm gần nhau trên trục x mà lại nhóm những điểm tại đó giá trị của hàm số gần nhau.
Điều này cho phép ta mở rộng ngay khái niệm tích phân ra một lớp hàm rất tổng qt.
Ngồi ra tích phân Lebesgue được định nghĩa hồn tồn như nhau đối với các khơng
gian có độ đo tùy ý, trong khi đó đầu tiên ta phải định nghĩa tích phân Riemann đối
với các hàm số một biến số, rồi sau đó mới mở rộng, với những sự thay đổi cần thiết

ra các hàm nhiều biến số. Đối với các hàm xác định trên khơng gian có độ đo trừu
tượng thì tích phân Riemann hồn tồn khơng có ý nghĩa. Khái niệm tích phân
Riemann được biết đến trong giáo trình giải tích và tốn cao cấp chỉ được áp dụng
cho những hàm liên tục hoặc khơng có q nhiều điểm gián đoạn. Riêng đối với
những hàm đo được thì chúng có thể gián đoạn khắp nơi trên miền xác định, do đó
phép xây dựng tích phân Riemann là khơng thể áp dụng được. Trong lúc đó, các yêu
cầu của những ngành khoa học kỹ thuật lại cần đến tích phân của những hàm không bị
chặn cũng như những hàm khơng liên tục tại một điểm nào đó. Vì vậy cần có một tích
phân hồn hảo, mềm dẻo hơn nhiều và tích phân Lebesgue là một hướng nhằm đáp
ứng các u cầu đó.
Do đó, chúng tơi ln có mong muốn đi sâu hơn về vấn đề này để bổ sung và
hồn thiện thêm kiến thức của mình qua “Chương 1: Tích phân Lebesgue”.
2. Mục đích nghiên cứu
- Hệ thống các tính chất của tích phân Lebesgue, tìm hiểu các điều kiện khả tích
(L), xét tính khả tích (L) của các hàm đo được. Nghiên cứu sâu hơn các tính chất liên
quan đến tính khả tích (L).
- Giải một số bài tốn về tích phân Lebesgue. Chẳng hạn: tính tích phân (L) bằng
cách sử dụng các hàm đơn giản, hàm tương đương, tính -cộng tính, tính chất của độ
đo, định lý hội tụ đơn điệu, định lý hội tụ bị chặn.
Trang 3


- Giải một số bài toán liên quan đến qua giới hạn dưới dấu tích phân.
- Giải các bài tốn liên quan đến điều kiện khả tích của các hàm đo được.
3. Phạm vi nghiên cứu
Tích phân Lebesgue: Các tính chất, các dạng tốn liên quan đến tích phân
Lebesgue.
4. Phương pháp nghiên cứu
- Tổng hợp, tham khảo các tài liệu có liên quan đến đề tài.
- Hệ thống những kiến thức cần thiết, cơ sở để tiếp cận nội dung chính của đề tài.

- Kết hợp tự nghiên cứu, trao đổi, tham khảo ý kiến của giáo viên hướng dẫn.

Trang 4


NỘI DUNG
1. Tư tưởng tích phân Lebesgue
 Khái niệm tích phân Riemann được biết đến trong giáo trình giải tích và toán
cao cấp chỉ được áp dụng cho những hàm liên tục hoặc có khơng q nhiều điểm gián
đoạn. Riêng đối với những hàm đo được thì chúng có thể gián đoạn khắp nơi trên
miền xác định, do đó phép xây dựng tích phân Riemann là khơng thể áp dụng được.
Vì vậy cần có một tích phân mới hồn hảo, mềm dẻo hơn nhiều, đó chính là tích phân
Lebesgue.
 Tư tưởng của tích phân Lebesgue là nhóm những điểm trên trục Ox thành 1 tập
sao cho giá trị hàm của chúng gần bằng nhau. Điều này cho phép chúng ta mở rộng
ngay khái niệm tích phân ra một lớp hàm rất tổng quát. Lebesgue đã chứng minh được
rằng nếu một hàm khả tích Riemann trên một hình hộp đóng và bị chặn thì hàm đó
cũng khả tích theo nghĩa Lebesgue và tích phân Lebesgue trùng với tích phân
Riemann. Đây là cơ sở cho phép chúng ta tính được tích phân Lebesgue thơng qua
tích phân Riemann.
2. Các định nghĩa tích phân
2.1. Định nghĩa
Cho là một hàm đo được xác định trên và độ đo µ.
(1)

Nếu là hàm đơn giản khơng âm, nghĩa là với các tập đo được, đôi một

rời nhau, , khi đó tích phân của hàm đối với độ đo µ trên tập ký hiệu :
(2)

Nếu thì tồn tại dãy các hàm đơn giản , lúc đó tích phân của hàm trên

được định nghĩa:
(3)

Nếu và các tích phân , hữu hạn thì tích phân của hàm đối với độ đo trên

tập A kí hiệu:

Trang 5


(4)

Nếu hữu hạn thì ta nói khả tích trên A . Như vậy khả tích trên A khi và

chỉ khi và cùng khả tích trên A.
(5)

Nếu là độ đo Lebesgue thì được gọi là tích phân Lebesgue và được ký

hiệu (L) .
??
?
Hãy giải thích tại sao và
Giải:
 Ta cần chứng minh )
Ta có:
Xét trên A:

 Ta cần chứng minh

Xét trên A:

2.2. Định lí
i. Nếu và đo được trên A thì .
ii. Nếu và đo được và bị chặn ở trên A thì khả tích trên A.
Chứng minh:
i. Ta nhận thấy rằng nếu là hàm đơn giản khơng âm thì

Trang 6


(Vì mọi tập con đo được của A đều có độ đo 0).
Từ đó dễ dàng suy ra:
Với là hàm đo được khơng âm và do đó suy ra kết quả cho là hàm đo được tùy ý.
ii. Xét ≥ 0.
Lúc đó tồn tại K > 0 sao cho 0 ≤ ≤ K trên A.
Theo định lí về cấu trúc hàm đo được tồn tại dãy đơn giản không âm, đơn điệu
tăng và hội tụ về .
Do đó và nên:
??
?
Tích phân với A= và là hàm Dirichlet.
Giải:
có dạng:
Ta có đo được, có hai giá trị là 0 và 1.
là hàm đơn giản
Xét đoạn ta có:

3. Các tính chất sơ cấp
3.1. Tính chất (giả sử các tích phân có nghĩa )
(1) Nếu thì (Cộng tính).
(2) Nếu thì .
(3) Nếu (Tuyến tính ).
(4) trên A thì (Bảo tồn thứ tự).
(5) trên A thì (Bảo tồn thứ tự).
Chứng minh:
Trang 7


(1)Ta chứng minh cho trường hợp vế trái có nghĩa.
i. là hàm đơn giản khơng âm trên . Lúc đó:
Và các đơi một rời nhau.
Ta có:
Và hai tập ở vế phải rời nhau. Do đó:
ii.
Lúc đó tồn tại dãy hàm đơn giản không âm tăng và hội tụ về .
Ta có:
Cho ta được:
iii. Ta phân tích
Theo ii) ta có

Nếu có nghĩa thì vế trái của một trong hai đẳng thức trên hữu hạn, do đó các hiện
số
đều có nghĩa. Do đó trừ vế theo vế hai đẳng thức trên ta được
Trường hợp có nghĩa cũng chứng minh tương tự.

(2)Nếu A và B rời nhau thì nên theo định lí trên
Trang 8

Cịn nếu A và B khơng rời nhau thì
và vì nên
(3) Đẳng thức này đã đúng khi Để hoàn thành chứng minh đẳng thức này, ta chứng
minh mệnh đề sau :
Nếu sao cho có nghĩa , thì
Thật vậy , gọi . Ta suy ra và nên
.
Do đó . Vậy

Do đó có nghĩa nên
Bây giờ chúng ta đã sẵn sàng cho việc chứng minh đẳng thức thứ hai trong trường
hợp tổng quát. Với tùy ý, ta có các biểu diễn và Theo giả thiết biểu thức sau là có
nghĩa
Do đó, cả bốn tích phân của các hàm đều hữu hạn hoặc và hai tích phân của là
hữu hạn hoặc
và hai tích phân của là hữu hạn.
Như vậy ,ta viết được:

Theo mệnh đề vừa chứng minh thì

Trang 9


Như vậy, tính chất tuyến tính của tích phân đã được chứng minh.
(4) Đặt thì nên theo (2) ta có:
Suy ra:
Tính chất trên cho ta thấy rằng khi ta thay đổi giá trị của hàm số trên một số trên
một tập hợp có độ đo 0 thì ta khơng làm thay đổi giá trị của tích phân. Cũng vì lý do

đó mà nếu một hàm số đo được trên tập hợp mà thì dù khơng xác định trên ta vẫn
định nghĩa .
(5)

Nếu và đều là hàm đơn giản thì điều đó đã được chứng minh bởi bổ đề 1. Nếu

trên A thì tồn tại những dãy hàm đơn giản khơng âm trên A. Do , ta có thể giả sử với
mọi (chỉ cần chọn theo chứng minh định lí về cấu trúc của hàm đo được).

Khi đó:
Cho ta được
Cuối cùng nếu thì ta suy ra và nên
Từ đó suy ra
Hay
3.2. Tính chất (Khả tích )
(1) Nếu có nghĩa thì
(2) khả tích trên A khi và chỉ khi khả tích trên A.
Trang 10


(3) Nếu hầu khắp nơi trên A và g khả tích trên A thì cũng khả tích trên A.
(4) Nếu khả tích trên A thì cũng khả tích trên A. Nếu khả tích trên A, bị chặn trên A
thì cũng khả tích trên A.
Chứng minh :
(1) Ta có :

Do đó:
(2) Do và nên khả tích trên A khi và chỉ khi khả tích trên A.
(3) Vì g hầu khắp nơi trên A nên
Vậy khả tích và do đó khả tích.

(4) Theo tính chất tuyến tính của tích phân ta suy ra g khả tích nếu và khả tích.
Ngồi ra nếu khả tích và g bị chặn thì nên
4. Bài tập
Bài tập 1. Cho là một hàm khả tích trên A và . Chứng minh:
Giải:
Đặt B = { A : }. Ta cần chứng minh () A.
Ta có có khả tích trên A khả tích trên A
<+
Mà (B) =
Mà = = +
Suy ra (B)
Do đó (B) < + (vì ) đpcm.

Trang 11


Bài tập 2. Cho là một hàm khả tích trên A. Chứng minh hữu hạn hầu khắp nơi trên
A.
Giải:
Đặt B = { A : = +}. Ta cần chứng minh (B) = 0.
Ta có khả tích trên A khả tích trên A
<+
B: = + ( > 0)
> 0 ta có: M(B) =
Mà = = +
Suy ra (B)
Do đó (B)
Cho M + suy ra (B) 0. Do đó (B) = 0.
Vậy hữu hạn hầu khắp nơi.
Bài tập 3. Cho trên A và . Chứng minh hầu khắp nơi trên A.

Giải:
Đặt B = { A : > 0}. Ta cần chứng minh (B) = 0.
Vì nên B = { A : 0}
=
Suy ra(B) =
Mà =
Ta có = = +
Suy ra ()
Do đó ()
Suy ra (B) = 0. Khi đó (B) 0 nên (B) = 0.
Vậy = 0 hữu hạn hầu khắp nơi trên A.

Trang 12


Chương 2: QUA GIỚI HẠN DƯỚI DẤU TÍCH PHÂN
1. Lý do chọn đề tài:
Các định lý qua giới hạn dưới dấu tích phân là phần quan trọng nhất của tích phân
Lebesgue và nó cũng là một trong những ưu điểm nổi bật của tích phân Lebesgue so
với tích phân Riemann.
Khi nghiên cứu tích phân, người ta ln quan tâm tới vấn đề qua giới hạn dưới dấu
tích phân, nghĩa là tìm điều kiện để có đẳng thức:
trong giải tích cổ điển, chúng ta biết rằng đối với tích phân Riemann thì điều kiện để:
thơng thường phải u cầu dãy hàm hội tụ đều trên miền lấy tích phân và nói chung
là một điều kiện khá chặt chẽ, rất khó thực hiện được, nên đây là một trong những hạn
chế của tích phân Riemann. Tuy nhiên đối với tích phân Lebesgue đẳng thức trên có
thể xảy ra với một số điều kiện rộng hơn, các điều kiện này thường gặp trong nhiều
vấn đề khác nhau của toán học. Và đối với tích phân Lebesgue, điều kiện để chuyển
giới hạn qua dấu tích phân là nhẹ nhàng và dễ thực hiện hơn.
Vì muốn nắm rõ vấn đề này nên chúng tơi tìm hiểu qua “ Chương 2: Qua giới hạn

dưới dấu tích phân” đối với tích phân Lebesgue.
2. Mục đích nghiên cứu
- Tìm hiểu về định lý Lêvi
- Định lý về sự hội tụ đơn điệu
- Định lý Lebesgue về sự hội tụ bị chặn
- Phương pháp tính tích phân Lebesgue
- Giải một số bài toán liên quan đến qua giới hạn dưới dấu tích phân.

3. Phạm vi nghiên cứu
Trang 13


- Qua giới hạn dưới hạn dưới dấu tích phân: các tính chất, các định lý, các dạng
tốn liên quan.
4. Phương pháp nghiên cứu
- Tập hợp, tham khảo các tài liệu có liên quan đến đề tài.
- Hệ thống những kiến thức cần thiết, cơ sở để tiếp cận nội dung chính của đề tài.
- Kết hợp tự nghiên cứu, trao đổi, tham khảo ý kiến của giáo viên hướng dẫn.

Trang 14


NỘI DUNG
1. Định lí Lêvi
Nếu thì
Chứng minh:
Nếu mọi đều là hàm đơn giản thì đẳng thức cần chứng minh chỉ là định nghĩa của
tích phân. Trường hợp bất kì thì với mỗi tồn tại một dãy hàm đơn giản không âm .
Do nên có thể xem . Vậy với ta có:
và do đó

Cho ta được:
Cho ta lại được:
Như vậy:
Nhưng đơn giản và với mọi nên:
Tóm lại:

Bài tập 4. Cho đo được trên A. Với mỗi ta đặt
Chứng minh rằng nếu f hữu hạn hầu khắp nơi trên A thì
Giải:
Đặt
Trang 15


vì hữu hạn hầu khắp nơi trên A.
Mà:
Vì nên
Chứng minh:
Trường hợp 1:

Hay:
Trường hợp 2:

Do đó:
Chứng minh:
ta ln có
Hay sao cho
Theo định nghĩa giới hạn:
Theo định lý Lêvi, ta có:
Bài tập 5. Cho trên A. Chứng minh rằng:
Giải:

Đặt . Chứng minh
Ta có:

Trang 16


Chứng minh:
Do đó:
Áp dụng định lý Lêvi, ta có:

2. Định lí về sự hội tụ đơn điệu
Nếu và khả tích trên A thì
Chứng minh:
Ta có nên theo định lí Lêvi

Do

�f1

A

hữu hạn nên:

Từ đây suy ra:
Chú ý: Nếu và khả tích thì định lí vẫn đúng
3. Định lí Lebesgue về sự hội tụ bị chặn
Nếu với g khả tích trên A và (hầu khắp nơi hay theo độ đo ) thì:

Chứng minh:
a) Trường hợp hầu khắp A.

Vì nên . Theo bổ đề Fatou ta có
,
Như vậy .
Nhưng = = nên .
Trang 17


Vậy =

b) Trường hợp trên A.
Theo định nghĩa của giới hạn trên tồn tại một dãy sao cho . Dãy hội tụ theo độ đo
về hàm nên có dãy con hội tụ về hầu khắp nơi . Theo phần a) ta có.
.
Tương tự như vậy ta chứng minh được
Nên
Bài tập 6. Cho và (hầu khắp nơi hay theo độ đo ). Chứng minh: nếu thì :
Giải:
Xét
Ta có:
Để có:
Ta chứng minh khả tích trên .
Ta có:
khả tích trên (đpcm).
4. Một số phương pháp tính tích phân Lebesgue
4.1. Định lí 4.1 (định lí so sánh)

Trang 18


Nếu một hàm khả tích Riemann trên một hình hộp đóng và bị chặn thì f cũng khả

tích Lebesgue và hai tích phân đó bằng nhau

Chứng minh:
Ta giới hạn việc chứng minh cho trường hợp = 1 và Xét một phân hoạch của []
thành phần bởi những điểm + và các tổng Dorbonx tương ứng  n = ;
trong đó:
Theo định nghĩa của tích phân Riemann, ta có
Ta định nghĩa
Tại , các hàm được xác định một cách tùy ý. Lúc đó

�f

n

[a ,b ]

= n ,

�f

n

[a ,b ]

=

Do dãy khơng tăng dãy không giảm và (x) hầu khắp nơi nên
Do đó

�f

[a ,b ]

Ta suy ra

= =

�f  f

[a ,b ]

�f

[a ,b ]

= (L)

�f  f

[a ,b ]

=0

Nên hầu khắp tức là
Vậy
??
?
Cho . Tính
Giải:
Đặt

Vì nên
Trang 19


Xét liên tục trên
khả tích Rieman trên
Theo định lý so sánh:
Đặt
Vì
Nên
Xét liên tục trên
khả tích Rieman trên
Theo định lý so sánh ta có:
4.2. Bài tốn tích phân
Cho Cần tính tích phân
(1)

Nếu đơi một rời nhau thì

(2)

Nếu và trên A thì

Chú ý: Khi tính tích phân Lebesgue ta thường phân tích một nửa khoảng hoặc
một khoảng thành các đoạn con lồng nhau hoặc rời nhau tùy theo dữ kiện của hàm
như sau:

,ℝ=
đơi một rời nhau,…
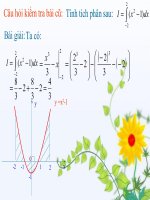
Ví dụ mẫu: Tính tích phân

Giải:
Cách 1:
Ta có: với tăng lồng nhau, nghĩa là:
...
Trang 20


Ta có ,
Suy ra
=
=
=
=

Cách 2:
Ta có với ( đơi một rời nhau.
Ta có ,
I=
=
=
=
=
=
=
=
Bài tập 7. Kí hiệu chỉ phần nguyên của x tức là số nguyên sao cho Tính các tích
phân Lebesgue sau:
a.
b.
c.

Giải:
a. .
Ta có: với đơi một rời nhau.
Trang 21


= > 0, x
Xét
Trong ta có:
Suy ra

=

Do đó =
= =
= =
=
Vậy
b.
Ta có: với đơi một rời nhau.
= > 0, x
Xét
Trong ta có:
Suy ra , do đó = n.(n+1)
=
= = = =
Suy ra =
= = =1
Vậy = 1.
c. .

Ta có: với đôi một rời nhau.
= > 0, x
Xét
Trang 22


Trong ta có:
Suy ra [x] = do đó =
=
= = = =
Suy ra =
= 1+ (
Ta có khai triển Taylor:
Chọn
Vậy .

Bài tập 8. Tính tích phân Lebesgue sau:
Giải:
a.
Ta có: với dãy tăng.

b.
Ta có: với dãy tăng.

Trang 23


Bài tập 9. Tính tích phân Lebesgue sau trên đoạn
a.
b. g

Giải:
a. Xét trên

Vì đếm được nên
Vì đếm được nên
Xét liên tục trên
khả tích Riemann trên
Theo định lí so sánh
khả tích Lebesgue trên
Và
b. Xét trên

Trang 24