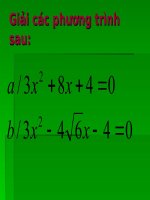Gián án Tiết 55: Công thức nghiệm thu gọn

TiÕt 55: C«ng thøc nghiÖm thu gän
Nga s¬n thanh hãa–

KIỂM TRA BÀI CŨ
3x
2
+ 8x + 4 = 0
2
2
a = 3; b = 8; c = 4
Δ= b -4ac
= 8 -4.3.4 = 16>0
Vì > 0 nên phương trình
có 2 nghiệm phân biệt:
Δ
1
2
8 4 2
2 2.3 3
8 4
2
2 2.3
b
x
a
b
x
a
− + ∆ − + −
= = =

− − ∆ − −
= = = −
Giải phương trình sau bằng cách
dùng công thức nghiệm:
HS 2
ViÕt c«ng thøc nghiÖm cña ph­¬ng
tr×nh bËc hai ax
2
+ bx + c = 0 ( a 0)
≠
HS 1
− + ∆
b
2a
x
1
=
− − ∆
b
2a
x
2
=
+ Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt:
+ Nếu ∆ = 0 thì phương trình có nghiệm kép:
+ Nếu ∆ < 0 thì phương trình vô nghiệm.
x
1
= x
2

=
−
b
2a
Đối với phương trình ax
2
+ bx + c = 0 (a ≠ 0)
và Δ = b
2
– 4ac :
Lêi gi¶i:

§ 5. CÔNG THỨC NGHIỆM THU GỌN
Tiết 55
1. C«ng thøc nghiÖm thu gän:

PHIẾU HỌC TẬP
Cho ph­¬ng tr×nh ax
2
+ bx + c = 0 (a 0) ; b = 2b
’
, Δ = 4 Δ’
Điền vào các chỗ trống (…) để được kết quả đúng:
+ Nếu Δ’ > 0 thì Δ …0 (khi đó ),phương trình có ………………….…….
... '∆ = ∆
1
..... .......
..................
2 2
b

x
a a
− + ∆ +
= = =
2
..... .......
..................
2 2
b
x
a a
− − ∆ −
= = =
+ Nếu Δ’ = 0 thì Δ …0, phương trình có …………….
1 2
......
..........
2 2
b
x x
a a
−
= = = =
+ Nếu Δ’ < 0 thì Δ …0, phương trình ……………
2 '∆
2 '∆
hai nghiệm phân biệt
nghiệm kép
vô nghiệm
>

<
=
2 'b
−
'b
a
−
2
≠
-2b
/
-
2b
/
a
+
∆
-b
/
a
−
∆
-b
/

§ 5. CÔNG THỨC NGHIỆM THU GỌN
Tiết 55
1. CÔNG THỨC NGHIỆM THU GỌN
− + ∆
b' '

a
x
1
=
− − ∆
b' '
a
x
2
=
+ Nếu ∆’ > 0 thì phương trình có hai nghiệm phân biệt:
+ Nếu ∆’ = 0 thì phương trình có nghiệm kép:
+ Nếu ∆’ < 0 thì phương trình vô nghiệm.
x
1
= x
2
=
−
b'
a
Đối với phương trình ax
2
+ bx + c = 0 (a ≠ 0)
và b = 2b’, Δ’ = b’
2
– ac :
− + ∆
b
2a

x
1
=
− − ∆
b
2a
x
2
=
+ Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt:
+ Nếu ∆ = 0 thì phương trình có nghiệm kép:
+ Nếu ∆ < 0 thì phương trình vô nghiệm.
x
1
= x
2
=
−
b
2a
Đối với phương trình ax
2
+ bx + c = 0 (a ≠ 0)
và Δ = b
2
– 4ac :
CÔNG THỨC NGHIỆM