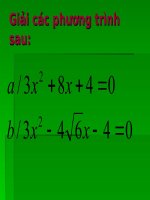CONG THUC NGHIEM THU GON NGUYEN TAN LOC

<span class='text_page_counter'>(1)</span>

<span class='text_page_counter'>(2)</span> KIỂM TRA BÀI CŨ Câu hỏi :Viết công thức nghiệm của phương trình bậc hai ? Áp dụng : Giải phương trình : 5x2 + 4x – 1 =0. Phương trình ax2 + bx +c =0 (a ≠ 0) Và Δ = b2 – 4ac  Nếu Δ>0 thì phương trình có hai nghiệm phân biệt :  b  x1  ; 2a . . x2.  b   2a. Nếu Δ =0 thì phương trình có  b nghiệm kép: x1= x2 = 2a Nếu Δ <0 thì phương trình vô nghiệm. (a=5; b=4; c=-1) Δ=42 -4.5.(-1) =36>0.   36 6. Phương trình có hai nghiệm phân biệt:.  46 1 x1   ; 10 5 4 6 x1   1 10.

<span class='text_page_counter'>(3)</span> Tuần 29 -Tiết 55 §5 CÔNG THỨC NGHIỆM THU GỌN 1. Công thức nghiệm thu gọn.

<span class='text_page_counter'>(4)</span> Phương trình ax2 + bx + c = 0 (a ≠ 0 ) b = 2b’ Nếu b chẳn ta đặt Khi đó : Δ = b2 - 4ac = (2b’)2 – 4ac = 4b’2 – 4ac = 4 (b’2 – ac). Kí hiệu : Δ’=b’2 - ac Khi đó ta có : Δ = 4 Δ’ Rõ ràng Δ’ và Δ cùng dấu, tức nếu Δ’ >0 thì Δ>0; nếu Δ’=0 thì Δ=0; nếu Δ’ <0 thì Δ<0. HOẠT ĐỘNG NHÓM : Từ công thức nghiệm , hãy dùng các đẳng thức .  .   . . b = 2b’. Δ = 4 Δ’. để viết nghiệm của phương trình ax2 + bx + c =0 theo b’ và Δ’.

<span class='text_page_counter'>(5)</span> Phương trình ax2 + bx +c =0 (a ≠ 0) Và Δ = b2 – 4ac  Nếu Δ>0 thì phương trình có hai nghiệm phân biệt:  b  ; 2a  b   2a. x1  x2 . Nếu Δ =0 thì phương trình có nghiệm kép:. b x1= x2=2a . Nếu Δ <0 thì phương trình vô nghiệm. Phương trình ax2 + bx +c =0 (a≠0) Và Δ’ = b’ 2 – ac. Vì Δ = 4 Δ’ nên : • Nếu Δ’ >0 thì. Δ>0 phương trình có hai nghiệm. phân biệt: b   2b '  4 '  2b '  2  '   2a 2a 2a  b '  '  a x1 .  b   2 b '  4 '  2b '  2  '   2a 2a 2a  b '  '  a x1 . • Nếu Δ’=0 thì Δ=0 phương trình có nghiệm kép:. b  2b '  b' x1 x2    2a 2a a •Nếu Δ’ <0 thì Δ <0 phương trình vô nghiệm.

<span class='text_page_counter'>(6)</span> Tuần 29 -Tiết 55 §5 CÔNG THỨC NGHIỆM THU GỌN 1. Công thức nghiệm thu gọn : Đối với phương trình ax2 + bx +c =0 (a≠0) Và Δ’ = b’2 – ac :  Nếu Δ’ >0 thì phương trình có hai nghiệm phân biệt:  b '  ' x1  a •. ;.  b '  ' x2  a. Nếu Δ’=0 thì phương trình có nghiệm kép:  b' x1 x2  a. Nếu Δ’ <0 thì phương trình vô nghiệm •. 2.Áp dụng : Ví dụ 1: Giải phương trình. 5x2 +4x – 1 =0 aa=5 = ... b’=2 b’ = ... cc = = -1 ... 2 Δ’= 2 Δ’ =....- 5.(-1) = 9 '  ' .... 3. Nghiệm của Phương trình có phương hai nghiệm trìnhbiệt : : phân  2 3. 1.  ........; ; Xx1 = 5 5 1. 2 3  1 x2 =........ 5 x2 .

<span class='text_page_counter'>(7)</span> Tuần 29 -Tiết 55 §5 CÔNG THỨC NGHIỆM THU GỌN 1. Công thức nghiệm thu gọn : Đối với phương trình ax2 + bx +c =0 (a≠0) Và Δ’ = b’2 – ac :  Nếu Δ’ >0 thì phương trình có hai nghiệm phân biệt:  b '  ' x1  a •. ;.  b '  ' x2  a. Nếu Δ’=0 thì phương trình có nghiệm kép:  b' x1 x2  a. Nếu Δ’ <0 thì phương trình vô nghiệm •. 2.Áp dụng : Ví dụ 2: Giải phương trình. a) 3x2 + 8x + 4 =03; b’ = 4; c = ( a=. 4) Δ’=' 42 - 3.4 = 4 >0 =2 Phương trình có hai  4  2 phân 2 biệt : nghiệm. x1 . . 3 3 4 2 x2   2 3.

<span class='text_page_counter'>(8)</span> Tuần 29 -Tiết 55 §5 CÔNG THỨC NGHIỆM THU GỌN 1. Công thức nghiệm thu gọn : Đối với phương trình ax2 + bx +c =0 (a≠0) Và Δ’ = b’2 – ac :  Nếu Δ’ >0 thì phương trình có hai nghiệm phân biệt:  b '  ' x1  a •. ;.  b '  ' x2  a. Nếu Δ’=0 thì phương trình có nghiệm kép:  b' x1 x2  a. Nếu Δ’ <0 thì phương trình vô nghiệm •. 2.Áp dụng : Ví dụ 2: Giải phương trình. b) 7x 2.  6 2x  2 0. 2 (a = 7; b’ = -3 ; c =2 )2 Δ’ = (-3 )2 - 7 . 2 = 4>' 0 =2 Phương trình có hai nghiệm 3 2 phân  2 biệt:. x1 . 7. 3 2 2 x1  7.

<span class='text_page_counter'>(9)</span> Tuần 29 -Tiết 55 §5 CÔNG THỨC NGHIỆM THU GỌN 1. Công thức nghiệm thu gọn : Đối với phương trình ax2 + bx +c =0 (a≠0) Và Δ’ = b’2 – ac :  Nếu Δ’ >0 thì phương trình có hai nghiệm phân biệt:  b '  ' x1  a •. ;.  b '  ' x2  a. Nếu Δ’=0 thì phương trình có nghiệm kép:  b' x1 x2  a. Nếu Δ’ <0 thì phương trình vô nghiệm •. 2.Áp dụng : Ví dụ 2: Giải phương trình. c )4 x 2  4 x  1 0. (a = 4; b’ = 2 ; c =1 ) Δ’ = 22 - 4 . 1 = 0 ' =0 Phương trình có nghiệm kép:. 2 1 x1  x2   4 2.

<span class='text_page_counter'>(10)</span> PHƯƠNG TRÌNH ax2+bx + c =0 (a≠0). Công thức nghiệm. Δ=b2-4ac Δ> 0. Đặt x làm nhân tử chung. b 2a. Δ=0. x1 x2 . Δ< 0. PT vô nghiệm. ax2+bx =0 Cách giải.  b  x1  2a  b  x2  2a. Khuyết c Nghiệm. x1 0 b x2  a. Công thức thu gọn.  b '  ' x1  a  b '  ' x2  a. Δ’>0.  b' a. Δ’=0. PT vô nghiệm. Δ’<0. x1 x2 . Khuyết b. Δ’=b’2 ac. ax2 +c =0. Cách giải 2. ax  c  x 2 . c a. Nghiệm a và c trái dấu Pt có 2 nghiệm. x . c a. a và c cùng dấu ptvn.

<span class='text_page_counter'>(11)</span>

<span class='text_page_counter'>(12)</span>